In mathematics, the Whitney umbrella (or Whitney's umbrella, named after American mathematician Hassler Whitney, and sometimes called a Cayley umbrella) is a specific self-intersecting surface placed in three dimensions. It is the union of all straight lines that pass through points of a fixed parabola and are perpendicular to a fixed straight line, parallel to the axis of the parabola and lying on its perpendicular bisecting plane.
Whitney's umbrella can be given by the parametric equations in Cartesian coordinates
where the parameters u and v range over the real numbers. It is also given by the implicit equation
This formula also includes the negative z axis (which is called the handle of the umbrella).
Whitney's umbrella is a ruled surface and a right conoid. It is important in the field of singularity theory, as a simple local model of a pinch point singularity. The pinch point and the fold singularity are the only stable local singularities of maps from R2 to R3.
It is named after the American mathematician Hassler Whitney.
In string theory, a Whitney brane is a D7-brane wrapping a variety whose singularities are locally modeled by the Whitney umbrella. Whitney branes appear naturally when taking Sen's weak coupling limit of F-theory.
In mathematics, an equation is a formula that expresses the equality of two expressions, by connecting them with the equals sign =. The word equation and its cognates in other languages may have subtly different meanings; for example, in French an équation is defined as containing one or more variables, while in English, any well-formed formula consisting of two expressions related with an equals sign is an equation.
In mathematics, a parabola is a plane curve which is mirror-symmetrical and is approximately U-shaped. It fits several superficially different mathematical descriptions, which can all be proved to define exactly the same curves.
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. More precisely, a straight line is said to be a tangent of a curve y = f(x) at a point x = c if the line passes through the point (c, f ) on the curve and has slope f'(c), where f' is the derivative of f. A similar definition applies to space curves and curves in n-dimensional Euclidean space.
In geometry, a hyperboloid of revolution, sometimes called a circular hyperboloid, is the surface generated by rotating a hyperbola around one of its principal axes. A hyperboloid is the surface obtained from a hyperboloid of revolution by deforming it by means of directional scalings, or more generally, of an affine transformation.
In geometry, a paraboloid is a quadric surface that has exactly one axis of symmetry and no center of symmetry. The term "paraboloid" is derived from parabola, which refers to a conic section that has a similar property of symmetry.
In continuum mechanics, vorticity is a pseudovector field that describes the local spinning motion of a continuum near some point, as would be seen by an observer located at that point and traveling along with the flow. It is an important quantity in the dynamical theory of fluids and provides a convenient framework for understanding a variety of complex flow phenomena, such as the formation and motion of vortex rings.
In algebra, a quadratic function, a quadratic polynomial, a polynomial of degree 2, or simply a quadratic, is a polynomial function with one or more variables in which the highest-degree term is of the second degree.
In mathematics, a parametric equation defines a group of quantities as functions of one or more independent variables called parameters. Parametric equations are commonly used to express the coordinates of the points that make up a geometric object such as a curve or surface, in which case the equations are collectively called a parametric representation or parameterization of the object.
In geometry, a (general) conical surface is the unbounded surface formed by the union of all the straight lines that pass through a fixed point — the apex or vertex — and any point of some fixed space curve — the directrix — that does not contain the apex. Each of those lines is called a generatrix of the surface.
A cylinder has traditionally been a three-dimensional solid, one of the most basic of curvilinear geometric shapes. Geometrically, it can be considered as a prism with a circle as its base.
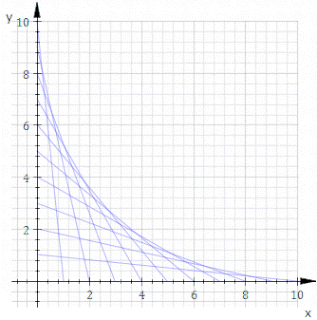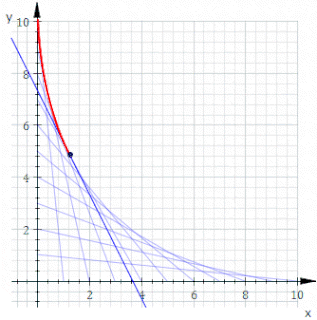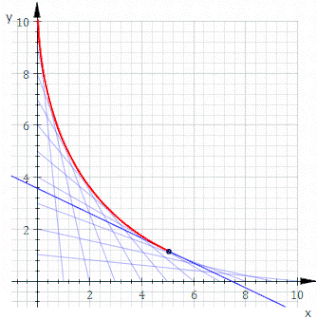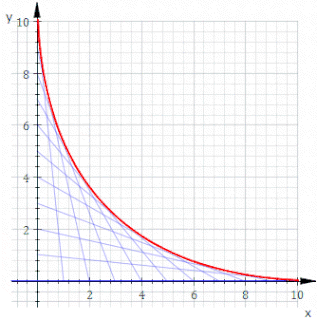
In geometry, an envelope of a planar family of curves is a curve that is tangent to each member of the family at some point, and these points of tangency together form the whole envelope. Classically, a point on the envelope can be thought of as the intersection of two "infinitesimally adjacent" curves, meaning the limit of intersections of nearby curves. This idea can be generalized to an envelope of surfaces in space, and so on to higher dimensions.
In applied mechanics, bending characterizes the behavior of a slender structural element subjected to an external load applied perpendicularly to a longitudinal axis of the element.
Euler–Bernoulli beam theory is a simplification of the linear theory of elasticity which provides a means of calculating the load-carrying and deflection characteristics of beams. It covers the case corresponding to small deflections of a beam that is subjected to lateral loads only. By ignoring the effects of shear deformation and rotatory inertia, it is thus a special case of Timoshenko beam theory. It was first enunciated circa 1750, but was not applied on a large scale until the development of the Eiffel Tower and the Ferris wheel in the late 19th century. Following these successful demonstrations, it quickly became a cornerstone of engineering and an enabler of the Second Industrial Revolution.
In mathematics, a surface is a mathematical model of the common concept of a surface. It is a generalization of a plane, but, unlike a plane, it may be curved; this is analogous to a curve generalizing a straight line.
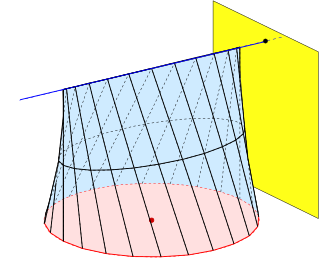
In geometry a conoid is a ruled surface, whose rulings (lines) fulfill the additional conditions
In mathematics, a conic section is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though historically it was sometimes called a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties.
In geometry, a pinch point or cuspidal point is a type of singular point on an algebraic surface.
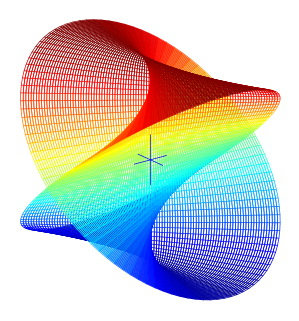
In geometry, a right conoid is a ruled surface generated by a family of straight lines that all intersect perpendicularly to a fixed straight line, called the axis of the right conoid.
In geometry, Plücker's conoid is a ruled surface named after the German mathematician Julius Plücker. It is also called a conical wedge or cylindroid; however, the latter name is ambiguous, as "cylindroid" may also refer to an elliptic cylinder.
In geometry, two conic sections are called confocal, if they have the same foci. Because ellipses and hyperbolas possess two foci, there are confocal ellipses, confocal hyperbolas and confocal mixtures of ellipses and hyperbolas. In the mixture of confocal ellipses and hyperbolas, any ellipse intersects any hyperbola orthogonally. Parabolas possess only one focus, so, by convention, confocal parabolas have the same focus and the same axis of symmetry. Consequently, any point not on the axis of symmetry lies on two confocal parabolas which intersect orthogonally.
