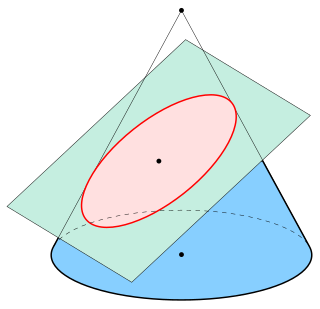
In mathematics, an ellipse is a plane curve surrounding two focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special type of ellipse in which the two focal points are the same. The elongation of an ellipse is measured by its eccentricity , a number ranging from to .

In mathematics, the Roman surface or Steiner surface is a self-intersecting mapping of the real projective plane into three-dimensional space, with an unusually high degree of symmetry. This mapping is not an immersion of the projective plane; however, the figure resulting from removing six singular points is one. Its name arises because it was discovered by Jakob Steiner when he was in Rome in 1844.

An ellipsoid is a surface that can be obtained from a sphere by deforming it by means of directional scalings, or more generally, of an affine transformation.
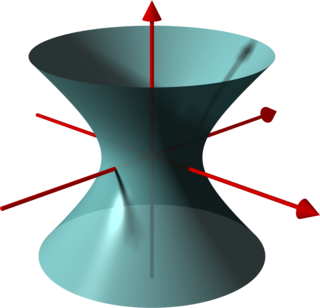
In geometry, a hyperboloid of revolution, sometimes called a circular hyperboloid, is the surface generated by rotating a hyperbola around one of its principal axes. A hyperboloid is the surface obtained from a hyperboloid of revolution by deforming it by means of directional scalings, or more generally, of an affine transformation.

In geometry, a catenoid is a type of surface, arising by rotating a catenary curve about an axis. It is a minimal surface, meaning that it occupies the least area when bounded by a closed space. It was formally described in 1744 by the mathematician Leonhard Euler.

In mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold; in other words, a one-sided surface. It cannot be embedded in standard three-dimensional space without intersecting itself. It has basic applications to geometry, since the common construction of the real projective plane is as the space of lines in R3 passing through the origin. The real projective plane is then an extension of the (ordinary) plane — to every point (v1,v2) of the ordinary plane, the line spanned by (v1,v2,1) is associated (i.e., the real projective plane is the projective completion of the ordinary plane, cf. also the homogeneous coordinates below) while there are also some “points in the infinity”.

In mathematics, a parametric equation defines a group of quantities as functions of one or more independent variables called parameters. Parametric equations are commonly used to express the coordinates of the points that make up a geometric object such as a curve or surface, called a parametric curve and parametric surface, respectively. In such cases, the equations are collectively called a parametric representation, or parametric system, or parameterization of the object.

The helicoid, also known as helical surface, after the plane and the catenoid, is the third minimal surface to be known.

In mathematics, a Dupin cyclide or cyclide of Dupin is any geometric inversion of a standard torus, cylinder or double cone. In particular, these latter are themselves examples of Dupin cyclides. They were discovered c. 1802 by Charles Dupin, while he was still a student at the École polytechnique following Gaspard Monge's lectures. The key property of a Dupin cyclide is that it is a channel surface in two different ways. This property means that Dupin cyclides are natural objects in Lie sphere geometry.
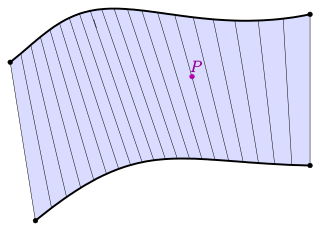
In geometry, a surface S is ruled if through every point of S there is a straight line that lies on S. Examples include the plane, the lateral surface of a cylinder or cone, a conical surface with elliptical directrix, the right conoid, the helicoid, and the tangent developable of a smooth curve in space.

A cone is a three-dimensional geometric shape that tapers smoothly from a flat base to a point called the apex or vertex.

In geometry, Villarceau circles are a pair of circles produced by cutting a torus obliquely through its center at a special angle.

In geometry, the Whitney umbrella or Whitney's umbrella, named after American mathematician Hassler Whitney, and sometimes called a Cayley umbrella, is a specific self-intersecting ruled surface placed in three dimensions. It is the union of all straight lines that pass through points of a fixed parabola and are perpendicular to a fixed straight line which is parallel to the axis of the parabola and lies on its perpendicular bisecting plane.
A parametric surface is a surface in the Euclidean space which is defined by a parametric equation with two parameters :\mathbb {R} ^{2}\to \mathbb {R} ^{3}} . Parametric representation is a very general way to specify a surface, as well as implicit representation. Surfaces that occur in two of the main theorems of vector calculus, Stokes' theorem and the divergence theorem, are frequently given in a parametric form. The curvature and arc length of curves on the surface, surface area, differential geometric invariants such as the first and second fundamental forms, Gaussian, mean, and principal curvatures can all be computed from a given parametrization.
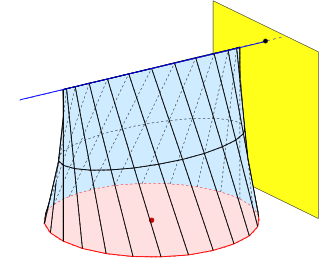
In geometry a conoid is a ruled surface, whose rulings (lines) fulfill the additional conditions:
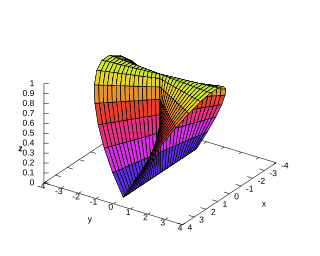
In geometry, Wallis's conical edge is a ruled surface given by the parametric equations

In geometry, Plücker's conoid is a ruled surface named after the German mathematician Julius Plücker. It is also called a conical wedge or cylindroid; however, the latter name is ambiguous, as "cylindroid" may also refer to an elliptic cylinder.
In geometry, central lines are certain special straight lines that lie in the plane of a triangle. The special property that distinguishes a straight line as a central line is manifested via the equation of the line in trilinear coordinates. This special property is related to the concept of triangle center also. The concept of a central line was introduced by Clark Kimberling in a paper published in 1994.

In geometry, a generalized helicoid is a surface in Euclidean space generated by rotating and simultaneously displacing a curve, the profile curve, along a line, its axis. Any point of the given curve is the starting point of a circular helix. If the profile curve is contained in a plane through the axis, it is called the meridian of the generalized helicoid. Simple examples of generalized helicoids are the helicoids. The meridian of a helicoid is a line which intersects the axis orthogonally.

In differential geometry a translation surface is a surface that is generated by translations: