In physics and geometry, a catenary is the curve that an idealized hanging chain or cable assumes under its own weight when supported only at its ends in a uniform gravitational field.

In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a reference point and an angle from a reference direction. The reference point is called the pole, and the ray from the pole in the reference direction is the polar axis. The distance from the pole is called the radial coordinate, radial distance or simply radius, and the angle is called the angular coordinate, polar angle, or azimuth. Angles in polar notation are generally expressed in either degrees or radians.

In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a given point in space is specified by three real numbers: the radial distancer along the radial line connecting the point to the fixed point of origin; the polar angleθ between the radial line and a polar axis; and the azimuthal angleφ as the angle of rotation of the radial line around the polar axis. (See graphic re the "physics convention".) Once the radius is fixed, the three coordinates (r, θ, φ), known as a 3-tuple, provide a coordinate system on a sphere, typically called the spherical polar coordinates.

In mathematics, an n-sphere or hypersphere is an -dimensional generalization of the -dimensional circle and -dimensional sphere to any non-negative integer . The circle is considered 1-dimensional, and the sphere 2-dimensional, because the surfaces themselves are 1- and 2-dimensional respectively, not because they exist as shapes in 1- and 2-dimensional space. As such, the -sphere is the setting for -dimensional spherical geometry.

In physics, angular velocity, also known as angular frequency vector, is a pseudovector representation of how the angular position or orientation of an object changes with time, i.e. how quickly an object rotates around an axis of rotation and how fast the axis itself changes direction.

An ellipsoid is a surface that can be obtained from a sphere by deforming it by means of directional scalings, or more generally, of an affine transformation.

In geometry, a hyperboloid of revolution, sometimes called a circular hyperboloid, is the surface generated by rotating a hyperbola around one of its principal axes. A hyperboloid is the surface obtained from a hyperboloid of revolution by deforming it by means of directional scalings, or more generally, of an affine transformation.
In mathematics, a unit vector in a normed vector space is a vector of length 1. A unit vector is often denoted by a lowercase letter with a circumflex, or "hat", as in .
In vector calculus, the Jacobian matrix of a vector-valued function of several variables is the matrix of all its first-order partial derivatives. When this matrix is square, that is, when the function takes the same number of variables as input as the number of vector components of its output, its determinant is referred to as the Jacobian determinant. Both the matrix and the determinant are often referred to simply as the Jacobian in literature. They are named after Carl Gustav Jacob Jacobi.
In the mathematical field of differential geometry, a metric tensor is an additional structure on a manifold M that allows defining distances and angles, just as the inner product on a Euclidean space allows defining distances and angles there. More precisely, a metric tensor at a point p of M is a bilinear form defined on the tangent space at p, and a metric field on M consists of a metric tensor at each point p of M that varies smoothly with p.
In calculus, the Leibniz integral rule for differentiation under the integral sign, named after Gottfried Wilhelm Leibniz, states that for an integral of the form where and the integrands are functions dependent on the derivative of this integral is expressible as where the partial derivative indicates that inside the integral, only the variation of with is considered in taking the derivative.

In mathematics, the Weierstrass–Enneper parameterization of minimal surfaces is a classical piece of differential geometry.

In geometry, a three-dimensional space is a mathematical space in which three values (coordinates) are required to determine the position of a point. Most commonly, it is the three-dimensional Euclidean space, that is, the Euclidean space of dimension three, which models physical space. More general three-dimensional spaces are called 3-manifolds. The term may also refer colloquially to a subset of space, a three-dimensional region, a solid figure.
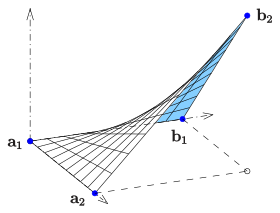
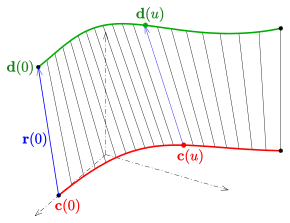
A parametric surface is a surface in the Euclidean space which is defined by a parametric equation with two parameters :\mathbb {R} ^{2}\to \mathbb {R} ^{3}} . Parametric representation is a very general way to specify a surface, as well as implicit representation. Surfaces that occur in two of the main theorems of vector calculus, Stokes' theorem and the divergence theorem, are frequently given in a parametric form. The curvature and arc length of curves on the surface, surface area, differential geometric invariants such as the first and second fundamental forms, Gaussian, mean, and principal curvatures can all be computed from a given parametrization.
In geometry a conoid is a ruled surface, whose rulings (lines) fulfill the additional conditions:

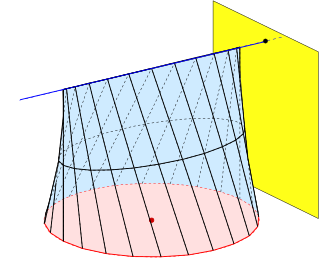
In geometry and topology, a channel or canal surface is a surface formed as the envelope of a family of spheres whose centers lie on a space curve, its directrix. If the radii of the generating spheres are constant, the canal surface is called a pipe surface. Simple examples are:

In mathematics, the differential geometry of surfaces deals with the differential geometry of smooth surfaces with various additional structures, most often, a Riemannian metric.
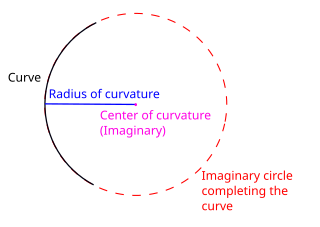
In differential geometry, the radius of curvature, R, is the reciprocal of the curvature. For a curve, it equals the radius of the circular arc which best approximates the curve at that point. For surfaces, the radius of curvature is the radius of a circle that best fits a normal section or combinations thereof.
In classical mechanics, the central-force problem is to determine the motion of a particle in a single central potential field. A central force is a force that points from the particle directly towards a fixed point in space, the center, and whose magnitude only depends on the distance of the object to the center. In a few important cases, the problem can be solved analytically, i.e., in terms of well-studied functions such as trigonometric functions.

In geometry, a generalized helicoid is a surface in Euclidean space generated by rotating and simultaneously displacing a curve, the profile curve, along a line, its axis. Any point of the given curve is the starting point of a circular helix. If the profile curve is contained in a plane through the axis, it is called the meridian of the generalized helicoid. Simple examples of generalized helicoids are the helicoids. The meridian of a helicoid is a line which intersects the axis orthogonally.







































![hyperboloid of one sheet for
ph
=
63
[?]
{\displaystyle \varphi =63^{\circ }} Regelfl-phi-h.svg](http://upload.wikimedia.org/wikipedia/commons/thumb/b/b1/Regelfl-phi-h.svg/280px-Regelfl-phi-h.svg.png)