
In geometry, a conical surface is a three-dimensional surface formed from the union of lines that pass through a fixed point and a space curve.

In geometry, a conical surface is a three-dimensional surface formed from the union of lines that pass through a fixed point and a space curve.
A (general) conical surface is the unbounded surface formed by the union of all the straight lines that pass through a fixed point — the apex or vertex— and any point of some fixed space curve — the directrix— that does not contain the apex. Each of those lines is called a generatrix of the surface. The directrix is often taken as a plane curve, in a plane not containing the apex, but this is not a requirement. [1]
In general, a conical surface consists of two congruent unbounded halves joined by the apex. Each half is called a nappe, and is the union of all the rays that start at the apex and pass through a point of some fixed space curve. [2] Sometimes the term "conical surface" is used to mean just one nappe. [3]
If the directrix is a circle , and the apex is located on the circle's axis (the line that contains the center of and is perpendicular to its plane), one obtains the right circular conical surface or double cone. [2] More generally, when the directrix is an ellipse, or any conic section, and the apex is an arbitrary point not on the plane of , one obtains an elliptic cone [4] (also called a conical quadric or quadratic cone), [5] which is a special case of a quadric surface. [4] [5]
A conical surface can be described parametrically as
where is the apex and is the directrix. [6]
Conical surfaces are ruled surfaces, surfaces that have a straight line through each of their points. [7] Patches of conical surfaces that avoid the apex are special cases of developable surfaces, surfaces that can be unfolded to a flat plane without stretching. When the directrix has the property that the angle it subtends from the apex is exactly , then each nappe of the conical surface, including the apex, is a developable surface. [8]
A cylindrical surface can be viewed as a limiting case of a conical surface whose apex is moved off to infinity in a particular direction. Indeed, in projective geometry a cylindrical surface is just a special case of a conical surface. [9]
In mathematics, analytic geometry, also known as coordinate geometry or Cartesian geometry, is the study of geometry using a coordinate system. This contrasts with synthetic geometry.

In mathematics, a parabola (/pɛər’əbəʊlə/) is a plane curve which is mirror-symmetrical and is approximately U-shaped. It fits several superficially different mathematical descriptions, which can all be proved to define exactly the same curves.

A sphere is a geometrical object that is a three-dimensional analogue to a two-dimensional circle. Formally, a sphere is the set of points that are all at the same distance r from a given point in three-dimensional space. That given point is the center of the sphere, and r is the sphere's radius. The earliest known mentions of spheres appear in the work of the ancient Greek mathematicians.
In mathematics, a quadric or quadric surface (quadric hypersurface in higher dimensions), is a generalization of conic sections (ellipses, parabolas, and hyperbolas). It is a hypersurface (of dimension D) in a (D + 1)-dimensional space, and it is defined as the zero set of an irreducible polynomial of degree two in D + 1 variables; for example, D = 1 in the case of conic sections. When the defining polynomial is not absolutely irreducible, the zero set is generally not considered a quadric, although it is often called a degenerate quadric or a reducible quadric.

In algebraic geometry, a Kummer quartic surface, first studied by Ernst Kummer (1864), is an irreducible nodal surface of degree 4 in with the maximal possible number of 16 double points. Any such surface is the Kummer variety of the Jacobian variety of a smooth hyperelliptic curve of genus 2; i.e. a quotient of the Jacobian by the Kummer involution x ↦ −x. The Kummer involution has 16 fixed points: the 16 2-torsion point of the Jacobian, and they are the 16 singular points of the quartic surface. Resolving the 16 double points of the quotient of a torus by the Kummer involution gives a K3 surface with 16 disjoint rational curves; these K3 surfaces are also sometimes called Kummer surfaces.

In geometry, the Dandelin spheres are one or two spheres that are tangent both to a plane and to a cone that intersects the plane. The intersection of the cone and the plane is a conic section, and the point at which either sphere touches the plane is a focus of the conic section, so the Dandelin spheres are also sometimes called focal spheres.

In mathematics, a Dupin cyclide or cyclide of Dupin is any geometric inversion of a standard torus, cylinder or double cone. In particular, these latter are themselves examples of Dupin cyclides. They were discovered c. 1802 by Charles Dupin, while he was still a student at the École polytechnique following Gaspard Monge's lectures. The key property of a Dupin cyclide is that it is a channel surface in two different ways. This property means that Dupin cyclides are natural objects in Lie sphere geometry.
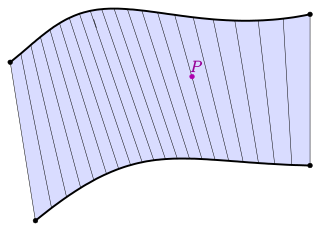
In geometry, a surface S is ruled if through every point of S there is a straight line that lies on S. Examples include the plane, the lateral surface of a cylinder or cone, a conical surface with elliptical directrix, the right conoid, the helicoid, and the tangent developable of a smooth curve in space.

A cone is a three-dimensional geometric shape that tapers smoothly from a flat base to a point called the apex or vertex.

A cylinder has traditionally been a three-dimensional solid, one of the most basic of curvilinear geometric shapes. In elementary geometry, it is considered a prism with a circle as its base.

In geometry, focuses or foci are special points with reference to which any of a variety of curves is constructed. For example, one or two foci can be used in defining conic sections, the four types of which are the circle, ellipse, parabola, and hyperbola. In addition, two foci are used to define the Cassini oval and the Cartesian oval, and more than two foci are used in defining an n-ellipse.

In geometry, a three-dimensional space is a mathematical space in which three values (coordinates) are required to determine the position of a point. Most commonly, it is the three-dimensional Euclidean space, that is, the Euclidean space of dimension three, which models physical space. More general three-dimensional spaces are called 3-manifolds. The term may also refer colloquially to a subset of space, a three-dimensional region, a solid figure.
In mathematics, enumerative geometry is the branch of algebraic geometry concerned with counting numbers of solutions to geometric questions, mainly by means of intersection theory.
A projective cone in projective geometry is the union of all lines that intersect a projective subspace R and an arbitrary subset A of some other subspace S, disjoint from R.

A conic section, conic or a quadratic curve is a curve obtained from a cone's surface intersecting a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though it was sometimes called as a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties.
The terminology of algebraic geometry changed drastically during the twentieth century, with the introduction of the general methods, initiated by David Hilbert and the Italian school of algebraic geometry in the beginning of the century, and later formalized by André Weil, Jean-Pierre Serre and Alexander Grothendieck. Much of the classical terminology, mainly based on case study, was simply abandoned, with the result that books and papers written before this time can be hard to read. This article lists some of this classical terminology, and describes some of the changes in conventions.

In geometry, an intersection curve is a curve that is common to two geometric objects. In the simplest case, the intersection of two non-parallel planes in Euclidean 3-space is a line. In general, an intersection curve consists of the common points of two transversally intersecting surfaces, meaning that at any common point the surface normals are not parallel. This restriction excludes cases where the surfaces are touching or have surface parts in common.

In mathematics, the intersection of two or more objects is another object consisting of everything that is contained in all of the objects simultaneously. For example, in Euclidean geometry, when two lines in a plane are not parallel, their intersection is the point at which they meet. More generally, in set theory, the intersection of sets is defined to be the set of elements which belong to all of them. Unlike the Euclidean definition, this does not presume that the objects under consideration lie in a common space.

In differential geometry Dupin's theorem, named after the French mathematician Charles Dupin, is the statement:

In mathematics, a quadric or quadric hypersurface is the subspace of N-dimensional space defined by a polynomial equation of degree 2 over a field. Quadrics are fundamental examples in algebraic geometry. The theory is simplified by working in projective space rather than affine space. An example is the quadric surface