
In geometry, every polyhedron is associated with a second dual structure, where the vertices of one correspond to the faces of the other, and the edges between pairs of vertices of one correspond to the edges between pairs of faces of the other. Such dual figures remain combinatorial or abstract polyhedra, but not all can also be constructed as geometric polyhedra. Starting with any given polyhedron, the dual of its dual is the original polyhedron.

In geometry, a polyhedron is a three-dimensional shape with flat polygonal faces, straight edges and sharp corners or vertices.
In elementary geometry, a polytope is a geometric object with flat sides (faces). Polytopes are the generalization of three-dimensional polyhedra to any number of dimensions. Polytopes may exist in any general number of dimensions n as an n-dimensional polytope or n-polytope. For example, a two-dimensional polygon is a 2-polytope and a three-dimensional polyhedron is a 3-polytope. In this context, "flat sides" means that the sides of a (k + 1)-polytope consist of k-polytopes that may have (k – 1)-polytopes in common.

In geometry, the convex hull or convex envelope or convex closure of a shape is the smallest convex set that contains it. The convex hull may be defined either as the intersection of all convex sets containing a given subset of a Euclidean space, or equivalently as the set of all convex combinations of points in the subset. For a bounded subset of the plane, the convex hull may be visualized as the shape enclosed by a rubber band stretched around the subset.

In Euclidean plane geometry, a rectangle is a quadrilateral with four right angles. It can also be defined as: an equiangular quadrilateral, since equiangular means that all of its angles are equal ; or a parallelogram containing a right angle. A rectangle with four sides of equal length is a square. The term "oblong" is occasionally used to refer to a non-square rectangle. A rectangle with vertices ABCD would be denoted as ABCD.

In geometry, the truncated cuboctahedron is an Archimedean solid, named by Kepler as a truncation of a cuboctahedron. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices, and 72 edges. Since each of its faces has point symmetry, the truncated cuboctahedron is a 9-zonohedron. The truncated cuboctahedron can tessellate with the octagonal prism.

In geometry, a truncated icosidodecahedron, rhombitruncated icosidodecahedron, great rhombicosidodecahedron, omnitruncated dodecahedron or omnitruncated icosahedron is an Archimedean solid, one of thirteen convex, isogonal, non-prismatic solids constructed by two or more types of regular polygon faces.

In geometry, the 24-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol {3,4,3}. It is also called C24, or the icositetrachoron, octaplex (short for "octahedral complex"), icosatetrahedroid, octacube, hyper-diamond or polyoctahedron, being constructed of octahedral cells.

In geometry, the midpoint is the middle point of a line segment. It is equidistant from both endpoints, and it is the centroid both of the segment and of the endpoints. It bisects the segment.

In solid geometry, the sphericon is a solid that has a continuous developable surface with two congruent, semi-circular edges, and four vertices that define a square. It is a member of a special family of rollers that, while being rolled on a flat surface, bring all the points of their surface to contact with the surface they are rolling on. It was discovered independently by carpenter Colin Roberts in the UK in 1969, by dancer and sculptor Alan Boeding of MOMIX in 1979, and by inventor David Hirsch, who patented it in Israel in 1980.

In geometry, a curve of constant width is a simple closed curve in the plane whose width is the same in all directions. The shape bounded by a curve of constant width is a body of constant width or an orbiform, the name given to these shapes by Leonhard Euler. Standard examples are the circle and the Reuleaux triangle. These curves can also be constructed using circular arcs centered at crossings of an arrangement of lines, as the involutes of certain curves, or by intersecting circles centered on a partial curve.

A Reuleaux triangle[ʁœlo] is a curved triangle with constant width, the simplest and best known curve of constant width other than the circle. It is formed from the intersection of three circular disks, each having its center on the boundary of the other two. Constant width means that the separation of every two parallel supporting lines is the same, independent of their orientation. Because its width is constant, the Reuleaux triangle is one answer to the question "Other than a circle, what shape can a manhole cover be made so that it cannot fall down through the hole?"

In geometry, the 16-cell is the regular convex 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol {3,3,4}. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century. It is also called C16, hexadecachoron, or hexdecahedroid [sic?].

A cone is a three-dimensional geometric shape that tapers smoothly from a flat base to a point called the apex or vertex.

In geometry, a pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex. Each base edge and apex form a triangle, called a lateral face. It is a conic solid with polygonal base. A pyramid with an n-sided base has n + 1 vertices, n + 1 faces, and 2n edges. All pyramids are self-dual.
In geometry, a polytope or a tiling is isotoxal or edge-transitive if its symmetries act transitively on its edges. Informally, this means that there is only one type of edge to the object: given two edges, there is a translation, rotation, and/or reflection that will move one edge to the other, while leaving the region occupied by the object unchanged.

An oloid is a three-dimensional curved geometric object that was discovered by Paul Schatz in 1929. It is the convex hull of a skeletal frame made by placing two linked congruent circles in perpendicular planes, so that the center of each circle lies on the edge of the other circle. The distance between the circle centers equals the radius of the circles. One third of each circle's perimeter lies inside the convex hull, so the same shape may be also formed as the convex hull of the two remaining circular arcs each spanning an angle of 4π/3.
In geometry, a polycon is a kind of a developable roller. It is made of identical pieces of a cone whose apex angle equals the angle of an even sided regular polygon. In principle, there are infinitely many polycons, as many as there are even sided regular polygons. Most members of the family have elongated spindle like shapes. The polycon family generalizes the sphericon. It was discovered by the Israeli inventor David Hirsch in 2017
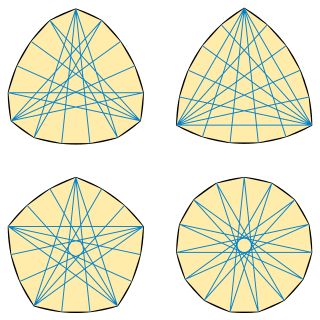
In geometry, a Reinhardt polygon is an equilateral polygon inscribed in a Reuleaux polygon. As in the regular polygons, each vertex of a Reinhardt polygon participates in at least one defining pair of the diameter of the polygon. Reinhardt polygons with sides exist, often with multiple forms, whenever is not a power of two. Among all polygons with sides, the Reinhardt polygons have the largest possible perimeter for their diameter, the largest possible width for their diameter, and the largest possible width for their perimeter. They are named after Karl Reinhardt, who studied them in 1922.


















