
In geometry, an n-gonal antiprism or n-antiprism is a polyhedron composed of two parallel direct copies of an n-sided polygon, connected by an alternating band of 2n triangles. They are represented by the Conway notation An.
In geometry, a bipyramid, dipyramid, or double pyramid is a polyhedron formed by fusing two pyramids together base-to-base. The polygonal base of each pyramid must therefore be the same, and unless otherwise specified the base vertices are usually coplanar and a bipyramid is usually symmetric, meaning the two pyramids are mirror images across their common base plane. When each apex of the bipyramid is on a line perpendicular to the base and passing through its center, it is a right bipyramid; otherwise it is oblique. When the base is a regular polygon, the bipyramid is also called regular.
In geometry, a Platonic solid is a convex, regular polyhedron in three-dimensional Euclidean space. Being a regular polyhedron means that the faces are congruent regular polygons, and the same number of faces meet at each vertex. There are only five such polyhedra:
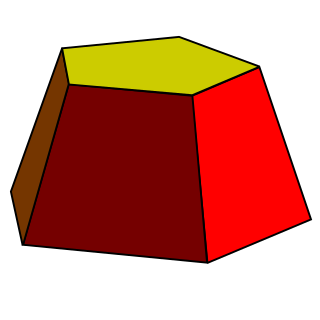
In geometry, a frustum ; is the portion of a solid that lies between two parallel planes cutting the solid. In the case of a pyramid, the base faces are polygonal and the side faces are trapezoidal. A right frustum is a right pyramid or a right cone truncated perpendicularly to its axis; otherwise, it is an oblique frustum. In a truncated cone or truncated pyramid, the truncation plane is not necessarily parallel to the cone's base, as in a frustum. If all its edges are forced to become of the same length, then a frustum becomes a prism.

In plane Euclidean geometry, a rhombus is a quadrilateral whose four sides all have the same length. Another name is equilateral quadrilateral, since equilateral means that all of its sides are equal in length. The rhombus is often called a "diamond", after the diamonds suit in playing cards which resembles the projection of an octahedral diamond, or a lozenge, though the former sometimes refers specifically to a rhombus with a 60° angle, and the latter sometimes refers specifically to a rhombus with a 45° angle.

In geometry, a prism is a polyhedron comprising an n-sided polygon base, a second base which is a translated copy of the first, and n other faces, necessarily all parallelograms, joining corresponding sides of the two bases. All cross-sections parallel to the bases are translations of the bases. Prisms are named after their bases, e.g. a prism with a pentagonal base is called a pentagonal prism. Prisms are a subclass of prismatoids.

In four-dimensional geometry, the 24-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol {3,4,3}. It is also called C24, or the icositetrachoron, octaplex (short for "octahedral complex"), icosatetrahedroid, octacube, hyper-diamond or polyoctahedron, being constructed of octahedral cells.

In geometry, a dodecagon, or 12-gon, is any twelve-sided polygon.

In solid geometry, the sphericon is a solid that has a continuous developable surface with two congruent, semi-circular edges, and four vertices that define a square. It is a member of a special family of rollers that, while being rolled on a flat surface, bring all the points of their surface to contact with the surface they are rolling on. It was discovered independently by carpenter Colin Roberts in the UK in 1969, by dancer and sculptor Alan Boeding of MOMIX in 1979, and by inventor David Hirsch, who patented it in Israel in 1980.

In Euclidean geometry, a square is a regular quadrilateral, which means that it has four straight sides of equal length and four equal angles. It can also be defined as a rectangle with two equal-length adjacent sides. It is the only regular polygon whose internal angle, central angle, and external angle are all equal (90°). A square with vertices ABCD would be denoted ABCD.

In geometry, the 16-cell is the regular convex 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol {3,3,4}. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century. It is also called C16, hexadecachoron, or hexdecahedroid [sic?].

In geometry, the 120-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol {5,3,3}. It is also called a C120, dodecaplex (short for "dodecahedral complex"), hyperdodecahedron, polydodecahedron, hecatonicosachoron, dodecacontachoron and hecatonicosahedroid.

A cone is a three-dimensional geometric shape that tapers smoothly from a flat base to a point called the apex or vertex.

In geometry, a triacontagon or 30-gon is a thirty-sided polygon. The sum of any triacontagon's interior angles is 5040 degrees.
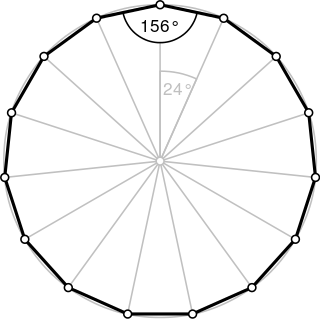
In geometry, a pentadecagon or pentakaidecagon or 15-gon is a fifteen-sided polygon.
In mathematics, a Coxeter element is an element of an irreducible Coxeter group which is a product of all simple reflections. The product depends on the order in which they are taken, but different orderings produce conjugate elements, which have the same order. This order is known as the Coxeter number. They are named after British-Canadian geometer H.S.M. Coxeter, who introduced the groups in 1934 as abstractions of reflection groups.
In geometry, a pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex. Each base edge and apex form a triangle, called a lateral face. A pyramid is a conic solid with a polygonal base. Many types of pyramids can be found by determining the shape of bases, either by based on a regular polygon or by cutting off the apex. It can be generalized into higher dimensions, known as hyperpyramid. All pyramids are self-dual.
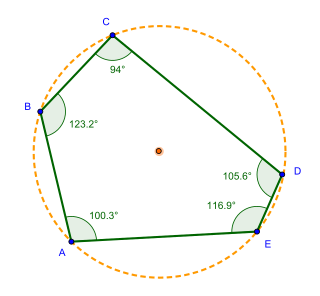
In geometry, a pentagon is any five-sided polygon or 5-gon. The sum of the internal angles in a simple pentagon is 540°.

In geometry, a developable roller is a convex solid whose surface consists of a single continuous, developable face. While rolling on a plane, most developable rollers develop their entire surface so that all the points on the surface touch the rolling plane. All developable rollers have ruled surfaces. Four families of developable rollers have been described to date: the prime polysphericons, the convex hulls of the two disc rollers, the polycons and the Platonicons.






















