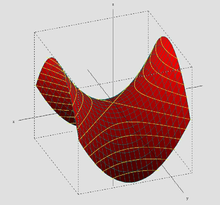
In analytic geometry, an asymptote of a curve is a line such that the distance between the curve and the line approaches zero as one or both of the x or y coordinates tends to infinity. In projective geometry and related contexts, an asymptote of a curve is a line which is tangent to the curve at a point at infinity.

In mathematics, an ellipse is a plane curve surrounding two focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special type of ellipse in which the two focal points are the same. The elongation of an ellipse is measured by its eccentricity , a number ranging from to .

In mathematics, a hyperbola is a type of smooth curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, that are mirror images of each other and resemble two infinite bows. The hyperbola is one of the three kinds of conic section, formed by the intersection of a plane and a double cone. If the plane intersects both halves of the double cone but does not pass through the apex of the cones, then the conic is a hyperbola.

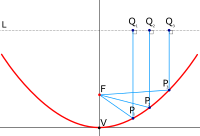
In mathematics, a parabola is a plane curve which is mirror-symmetrical and is approximately U-shaped. It fits several superficially different mathematical descriptions, which can all be proved to define exactly the same curves.

In mathematics, a partial differential equation (PDE) is an equation which computes a function between various partial derivatives of a multivariable function.

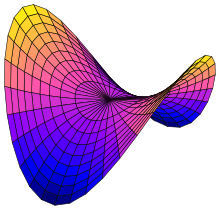
In mathematics, the Roman surface or Steiner surface is a self-intersecting mapping of the real projective plane into three-dimensional space, with an unusually high degree of symmetry. This mapping is not an immersion of the projective plane; however, the figure resulting from removing six singular points is one. Its name arises because it was discovered by Jakob Steiner when he was in Rome in 1844.

In geometry, a hyperboloid of revolution, sometimes called a circular hyperboloid, is the surface generated by rotating a hyperbola around one of its principal axes. A hyperboloid is the surface obtained from a hyperboloid of revolution by deforming it by means of directional scalings, or more generally, of an affine transformation.

In mathematics, a quadratic polynomial is a polynomial of degree two in one or more variables. A quadratic function is the polynomial function defined by a quadratic polynomial. Before the 20th century, the distinction was unclear between a polynomial and its associated polynomial function; so "quadratic polynomial" and "quadratic function" were almost synonymous. This is still the case in many elementary courses, where both terms are often abbreviated as "quadratic".

A parabolicreflector is a reflective surface used to collect or project energy such as light, sound, or radio waves. Its shape is part of a circular paraboloid, that is, the surface generated by a parabola revolving around its axis. The parabolic reflector transforms an incoming plane wave travelling along the axis into a spherical wave converging toward the focus. Conversely, a spherical wave generated by a point source placed in the focus is reflected into a plane wave propagating as a collimated beam along the axis.

Parabolic coordinates are a two-dimensional orthogonal coordinate system in which the coordinate lines are confocal parabolas. A three-dimensional version of parabolic coordinates is obtained by rotating the two-dimensional system about the symmetry axis of the parabolas.

In mathematics, a Dupin cyclide or cyclide of Dupin is any geometric inversion of a standard torus, cylinder or double cone. In particular, these latter are themselves examples of Dupin cyclides. They were discovered c. 1802 by Charles Dupin, while he was still a student at the École polytechnique following Gaspard Monge's lectures. The key property of a Dupin cyclide is that it is a channel surface in two different ways. This property means that Dupin cyclides are natural objects in Lie sphere geometry.
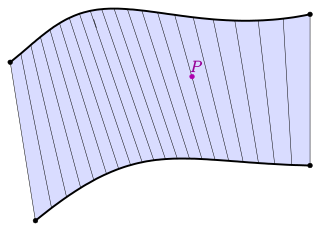
In geometry, a surface S is ruled if through every point of S there is a straight line that lies on S. Examples include the plane, the lateral surface of a cylinder or cone, a conical surface with elliptical directrix, the right conoid, the helicoid, and the tangent developable of a smooth curve in space.

A cone is a three-dimensional geometric shape that tapers smoothly from a flat base to a point called the apex or vertex.

A cylinder has traditionally been a three-dimensional solid, one of the most basic of curvilinear geometric shapes. In elementary geometry, it is considered a prism with a circle as its base.

In mathematics, the eccentricity of a conic section is a non-negative real number that uniquely characterizes its shape.

In geometry, a Cassini oval is a quartic plane curve defined as the locus of points in the plane such that the product of the distances to two fixed points (foci) is constant. This may be contrasted with an ellipse, for which the sum of the distances is constant, rather than the product. Cassini ovals are the special case of polynomial lemniscates when the polynomial used has degree 2.
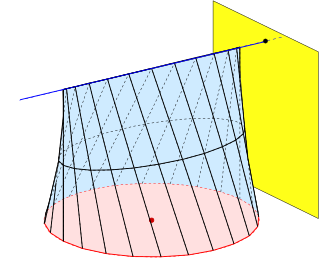
In geometry a conoid is a ruled surface, whose rulings (lines) fulfill the additional conditions:

A conic section, conic or a quadratic curve is a curve obtained from a cone's surface intersecting a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though it was sometimes called as a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties.

In geometry, two conic sections are called confocal if they have the same foci.

In geometry, a circular section is a circle on a quadric surface. It is a special plane section of the quadric, as this circle is the intersection with the quadric of the plane containing the circle.