 | This article needs additional citations for verification .(December 2023) |
In method ringing, a branch of change ringing, the ringing pattern known as plain hunt is the simplest method of generating continuously changing sequences, and is a fundamental building-block of method ringing. [1]
Plain hunting consists of a linear undeviating course of a bell between the first and last places in the striking order, with two strikes in the first and last position to enable a turn-around.
On eight bells this is shown in the accompanying diagram below, where all the bells are plain hunting. The bells are written out in their striking order, and each sequence is a "change":
Thus each bell moves one position at each succeeding change, unless they reach the first or last position, when they remain there for two changes then proceed to the other end of the sequence. [2]
This simple rule can be extended to any number of bells, so that on 12 bells for instance, 24 unique changes can be obtained.
Example – plain hunt on eight bells
1 2 3 4 5 6 7 8- start in rounds (rounds is the descending sequence of bells) 2 1 4 3 6 5 8 7 2 4 1 6 3 8 5 7 4 2 6 1 8 3 7 5 4 6 2 8 1 7 3 5 6 4 8 2 7 1 5 3 6 8 4 7 2 5 1 3 8 6 7 4 5 2 3 1 8 7 6 5 4 3 2 1 – reverse rounds 7 8 5 6 3 4 1 2 7 5 8 3 6 1 4 2 5 7 3 8 1 6 2 4 5 3 7 1 8 2 6 4 3 5 1 7 2 8 4 6 3 1 5 2 7 4 8 6 1 3 2 5 4 7 6 8 1 2 3 4 5 6 7 8 – finish in rounds
Plain hunt is limited to a small number of possible different changes, which is numerically equal to twice the number of bells that are hunting. However, by introducing deviations from the plain hunt, by causing some of the bells to change their relationship to the others, change ringing "methods" were developed. These allow a large range of possible different changes to be rung; even to the extent of the full factorial sequence of changes.
The diagram on the right shows how plain hunt is used as a building-block in other ringing methods.
Bell number 1 is always plain hunting (shown in blue), and the other bells plain hunt but they change their pattern when bell number 1 is the first bell in the sequence. An example of one bell which is deviating from plain hunt is shown in red.
This variation on plain hunt means that up to 60 changes can be rung without repetition in this case.
There are thousands of ringing methods which incorporate blocks of plain hunt, and are only distinguished by different deviations at set points. These deviations define a particular ringing method in change ringing.
In geometry, a convex uniform honeycomb is a uniform tessellation which fills three-dimensional Euclidean space with non-overlapping convex uniform polyhedral cells.
The unified modeling language (UML) is a general-purpose visual modeling language that is intended to provide a standard way to visualize the design of a system.
Change ringing is the art of ringing a set of tuned bells in a tightly controlled manner to produce precise variations in their successive striking sequences, known as "changes". This can be by method ringing in which the ringers commit to memory the rules for generating each change, or by call changes, where the ringers are instructed how to generate each change by instructions from a conductor. This creates a form of bell music which cannot be discerned as a conventional melody, but is a series of mathematical sequences. It can also be automated by machinery.
Campanology is the scientific and musical study of bells. It encompasses the technology of bells—how they are founded, tuned and rung—as well as the history, methods, and traditions of bellringing as an art.
A church bell is a bell in a church building designed to be heard outside the building. It can be a single bell, or part of a set of bells. Their main function is to call worshippers to the church for a communal service, but are also rung on special occasions such as a wedding, or a funeral service. In some Christian traditions they signify to people outside that a particular part of the service has been reached.
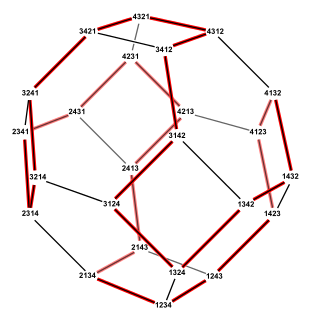
The Steinhaus–Johnson–Trotter algorithm or Johnson–Trotter algorithm, also called plain changes, is an algorithm named after Hugo Steinhaus, Selmer M. Johnson and Hale F. Trotter that generates all of the permutations of elements. Each two adjacent permutations in the resulting sequence differ by swapping two adjacent permuted elements. Equivalently, this algorithm finds a Hamiltonian cycle in the permutohedron, a polytope whose vertices represent permutations and whose edges represent swaps.
Method ringing is a form of change ringing in which the ringers commit to memory the rules for generating each change of sequence, and pairs of bells are affected. This creates a form of bell music which is continually changing, but which cannot be discerned as a conventional melody. It is a way of sounding continually changing mathematical permutations.
The Oxford University Society of Change Ringers, founded in 1872, is the official society dedicated to change ringing in Oxford University. Its objects are to promote the art of change ringing in the university and to ring for Sunday services in Oxford during full term.
A "ring of bells" is the name bell ringers give to a set of bells hung for English full circle ringing. The term "peal of bells" is often used, though peal also refers to a change ringing performance of more than about 5,000 changes.
In campanology, a peal is the special name given to a specific type of performance of change ringing which meets certain exacting conditions for duration, complexity and quality.
Relay logic is a method of implementing combinational logic in electrical control circuits by using several electrical relays wired in a particular configuration.
Grandsire is one of the standard change ringing methods, which are methods of ringing church bells or handbells using a series of mathematical permutations rather than using a melody. The grandsire method is usually rung on an odd number of bells: Grandsire doubles is rung on five working bells, grandsire triples on seven, grandsire caters on nine and grandsire cinques on eleven. Like all odd-bell methods, where there are sufficient bells, it is normally rung with a "cover" bell, which stays in the last position in each row to add musicality.
Call change ringing is a branch of the art of change ringing, in which a group of English-style full-circle bell ringers are instructed continually to create different sequences, or changes, of the bells' striking order. Each command from the leader or "conductor" of the ringing results in a new sequence of sounding the bells. Each sequence is repeated until the next command or "call".
In 8-dimensional geometry, the 142 is a uniform 8-polytope, constructed within the symmetry of the E8 group.
In 8-dimensional geometry, the 241 is a uniform 8-polytope, constructed within the symmetry of the E8 group.
A functional flow block diagram (FFBD) is a multi-tier, time-sequenced, step-by-step flow diagram of a system's functional flow. The term "functional" in this context is different from its use in functional programming or in mathematics, where pairing "functional" with "flow" would be ambiguous. Here, "functional flow" pertains to the sequencing of operations, with "flow" arrows expressing dependence on the success of prior operations. FFBDs may also express input and output data dependencies between functional blocks, as shown in figures below, but FFBDs primarily focus on sequencing.
A bell-ringer is a person who rings a bell, usually a church bell, by means of a rope or other mechanism.
Fabian Stedman (1640–1713) was an English author and a leading figure in the early history of campanology, particularly in the field of method ringing. He had a key role in publishing two books Tintinnalogia and Campanalogia which are the first two publications on the subject. He is also regarded as being a pioneer in the branch of mathematics known as Group theory.
Veronese bell ringing is a style of ringing church bells that developed around Verona, Italy, from the eighteenth century. The bells are rung full circle, being held up by a rope and wheel until a note is required.
The Australian and New Zealand Association of Bellringers, known as ANZAB, is the organisation responsible for the promotion of English-style "full circle ringing" – namely change ringing and method ringing in bell towers with a peal of bells – across Australia and New Zealand.
Dutton pulled out a notebook filled with handwritten sequences with names including, "Plain Hunt" and "Plain Bob." Numbers denote each bell's place in the variations.