In probability theory, a pregaussian class or pregaussian set of functions is a set of functions, square integrable with respect to some probability measure, such that there exists a certain Gaussian process, indexed by this set, satisfying the conditions below.
For a probability space (S, Σ, P), denote by a set of square integrable with respect to P functions , that is
Consider a set . There exists a Gaussian process , indexed by , with mean 0 and covariance
Such a process exists because the given covariance is positive definite. This covariance defines a semi-inner product as well as a pseudometric on given by
Definition A class is called pregaussian if for each the function on is bounded, -uniformly continuous, and prelinear.
The process is a generalization of the brownian bridge. Consider with P being the uniform measure. In this case, the process indexed by the indicator functions , for is in fact the standard brownian bridge B(x). This set of the indicator functions is pregaussian, moreover, it is the Donsker class.
In probability theory and statistics, a probability distribution is the mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. It is a mathematical description of a random phenomenon in terms of its sample space and the probabilities of events.
In probability, and statistics, a multivariate random variable or random vector is a list of mathematical variables each of whose value is unknown, either because the value has not yet occurred or because there is imperfect knowledge of its value. The individual variables in a random vector are grouped together because they are all part of a single mathematical system — often they represent different properties of an individual statistical unit. For example, while a given person has a specific age, height and weight, the representation of these features of an unspecified person from within a group would be a random vector. Normally each element of a random vector is a real number.
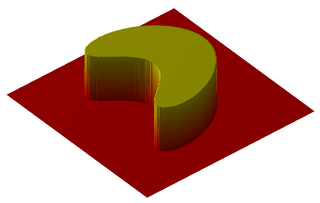
In mathematics, an indicator function or a characteristic function is a function defined on a set X that indicates membership of an element in a subset A of X, having the value 1 for all elements of A and the value 0 for all elements of X not in A. It is usually denoted by a symbol 1 or I, sometimes in boldface or blackboard boldface, with a subscript specifying the subset.
In probability theory and statistics, a Gaussian process is a stochastic process, such that every finite collection of those random variables has a multivariate normal distribution, i.e. every finite linear combination of them is normally distributed. The distribution of a Gaussian process is the joint distribution of all those random variables, and as such, it is a distribution over functions with a continuous domain, e.g. time or space.
In probability theory, the conditional expectation, conditional expected value, or conditional mean of a random variable is its expected value – the value it would take “on average” over an arbitrarily large number of occurrences – given that a certain set of "conditions" is known to occur. If the random variable can take on only a finite number of values, the “conditions” are that the variable can only take on a subset of those values. More formally, in the case when the random variable is defined over a discrete probability space, the "conditions" are a partition of this probability space.
In the theory of stochastic processes, the Karhunen–Loève theorem, also known as the Kosambi–Karhunen–Loève theorem is a representation of a stochastic process as an infinite linear combination of orthogonal functions, analogous to a Fourier series representation of a function on a bounded interval. The transformation is also known as Hotelling transform and eigenvector transform, and is closely related to principal component analysis (PCA) technique widely used in image processing and in data analysis in many fields.
In mathematics, mixing is an abstract concept originating from physics: the attempt to describe the irreversible thermodynamic process of mixing in the everyday world: mixing paint, mixing drinks, industrial mixing, etc.
In statistics and probability theory, a point process or point field is a collection of mathematical points randomly located on some underlying mathematical space such as the real line, the Cartesian plane, or more abstract spaces. Point processes can be used as mathematical models of phenomena or objects representable as points in some type of space.
In probability theory, Donsker's theorem, named after Monroe D. Donsker, is a functional extension of the central limit theorem.
In mathematics, a π-system on a set Ω is a collection P of certain subsets of Ω, such that
In probability theory, random element is a generalization of the concept of random variable to more complicated spaces than the simple real line. The concept was introduced by Maurice Fréchet (1948) who commented that the “development of probability theory and expansion of area of its applications have led to necessity to pass from schemes where (random) outcomes of experiments can be described by number or a finite set of numbers, to schemes where outcomes of experiments represent, for example, vectors, functions, processes, fields, series, transformations, and also sets or collections of sets.”
In the fields of actuarial science and financial economics there are a number of ways that risk can be defined; to clarify the concept theoreticians have described a number of properties that a risk measure might or might not have. A coherent risk measure is a function that satisfies properties of monotonicity, sub-additivity, homogeneity, and translational invariance.
In mathematics, progressive measurability is a property in the theory of stochastic processes. A progressively measurable process, while defined quite technically, is important because it implies the stopped process is measurable. Being progressively measurable is a strictly stronger property than the notion of being an adapted process. Progressively measurable processes are important in the theory of Itô integrals.
In probability theory and statistical mechanics, the Gaussian free field (GFF) is a Gaussian random field, a central model of random surfaces. Sheffield (2007) gives a mathematical survey of the Gaussian free field.
In mathematics, uniform integrability is an important concept in real analysis, functional analysis and measure theory, and plays a vital role in the theory of martingales. The definition used in measure theory is closely related to, but not identical to, the definition typically used in probability.
In probability theory, a random measure is a measure-valued random element. Random measures are for example used in the theory of random processes, where they form many important point processes such as Poisson point processes and Cox processes.
In mathematics — specifically, in stochastic analysis — an Itô diffusion is a solution to a specific type of stochastic differential equation. That equation is similar to the Langevin equation used in physics to describe the Brownian motion of a particle subjected to a potential in a viscous fluid. Itô diffusions are named after the Japanese mathematician Kiyosi Itô.
In probability theory and statistics, complex random variables are a generalization of real-valued random variables to complex numbers, i.e. the possible values a complex random variable may take are complex numbers. Complex random variables can always be considered as pairs of real random variables: their real and imaginary parts. Therefore, the distribution of one complex random variable may be interpreted as the joint distribution of two real random variables.
The Engelbert–Schmidt zero–one law is a theorem that gives a mathematical criterion for an event associated with a continuous, non-decreasing additive functional of Brownian motion to have probability either 0 or 1, without the possibility of an intermediate value. This zero-one law is used in the study of questions of finiteness and asymptotic behavior for stochastic differential equations. This 0-1 law, published in 1981, is named after Hans-Jürgen Engelbert and the probabilist Wolfgang Schmidt.
q-Gaussian processes are deformations of the usual Gaussian distribution. There are several different versions of this; here we treat a multivariate deformation, also addressed as q-Gaussian process, arising from free probability theory and corresponding to deformations of the canonical commutation relations. For other deformations of Gaussian distributions, see q-Gaussian distribution and Gaussian q-distribution.
