In the mathematics of graph theory and finite groups, a prime graph is an undirected graph defined from a group. These graphs were introduced in a 1981 paper by J. S. Williams, credited to unpublished work from 1975 by K. W. Gruenberg and O. Kegel. [1]
The prime graph of a group has a vertex for each prime number that divides the order (number of elements) of the given group, and an edge connecting each pair of prime numbers and for which there exists a group element with order . [1] [2]
Equivalently, there is an edge from to whenever the given group contains commuting elements of order and of order , [1] or whenever the given group contains a cyclic group of order as one of its subgroups. [2]
Certain finite simple groups can be recognized by the degrees of the vertices in their prime graphs. [3] The connected components of a prime graph have diameter at most five, and at most three for solvable groups. [4] When a prime graph is a tree, it has at most eight vertices, and at most four for solvable groups. [5]
Variations of prime graphs that replace the existence of a cyclic subgroup of order , in the definition for adjacency in a prime graph, by the existence of a subgroup of another type, have also been studied. [2] Similar results have also been obtained from a related family of graphs, obtained from a finite group through the degrees of its characters rather than through the orders of its elements. [6]
In mathematics, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on the order in which they are written. That is, the group operation is commutative. With addition as an operation, the integers and the real numbers form abelian groups, and the concept of an abelian group may be viewed as a generalization of these examples. Abelian groups are named after Niels Henrik Abel.
In the mathematical field of group theory, Lagrange's theorem states that if H is a subgroup of any finite group G, then |H| is a divisor of |G|, i.e. the order of every subgroup H divides the order of group G.
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, namely a nontrivial normal subgroup and the corresponding quotient group. This process can be repeated, and for finite groups one eventually arrives at uniquely determined simple groups, by the Jordan–Hölder theorem.
In abstract algebra, a cyclic group or monogenous group is a group, denoted Cn, that is generated by a single element. That is, it is a set of invertible elements with a single associative binary operation, and it contains an element g such that every other element of the group may be obtained by repeatedly applying the group operation to g or its inverse. Each element can be written as an integer power of g in multiplicative notation, or as an integer multiple of g in additive notation. This element g is called a generator of the group.
In mathematics, specifically in the field of finite group theory, the Sylow theorems are a collection of theorems named after the Norwegian mathematician Peter Ludwig Sylow that give detailed information about the number of subgroups of fixed order that a given finite group contains. The Sylow theorems form a fundamental part of finite group theory and have very important applications in the classification of finite simple groups.
In abstract algebra, a generating set of a group is a subset of the group set such that every element of the group can be expressed as a combination of finitely many elements of the subset and their inverses.
In mathematics, the Erdős–Ko–Rado theorem limits the number of sets in a family of sets for which every two sets have at least one element in common. Paul Erdős, Chao Ko, and Richard Rado proved the theorem in 1938, but did not publish it until 1961. It is part of the field of combinatorics, and one of the central results of extremal set theory.
In mathematics, a Coxeter group, named after H. S. M. Coxeter, is an abstract group that admits a formal description in terms of reflections. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; for example, the symmetry group of each regular polyhedron is a finite Coxeter group. However, not all Coxeter groups are finite, and not all can be described in terms of symmetries and Euclidean reflections. Coxeter groups were introduced in 1934 as abstractions of reflection groups, and finite Coxeter groups were classified in 1935.
In abstract algebra, a finite group is a group whose underlying set is finite. Finite groups often arise when considering symmetry of mathematical or physical objects, when those objects admit just a finite number of structure-preserving transformations. Important examples of finite groups include cyclic groups and permutation groups.
In mathematics, the Ihara zeta function is a zeta function associated with a finite graph. It closely resembles the Selberg zeta function, and is used to relate closed walks to the spectrum of the adjacency matrix. The Ihara zeta function was first defined by Yasutaka Ihara in the 1960s in the context of discrete subgroups of the two-by-two p-adic special linear group. Jean-Pierre Serre suggested in his book Trees that Ihara's original definition can be reinterpreted graph-theoretically. It was Toshikazu Sunada who put this suggestion into practice in 1985. As observed by Sunada, a regular graph is a Ramanujan graph if and only if its Ihara zeta function satisfies an analogue of the Riemann hypothesis.
In mathematics, a dessin d'enfant is a type of graph embedding used to study Riemann surfaces and to provide combinatorial invariants for the action of the absolute Galois group of the rational numbers. The name of these embeddings is French for a "child's drawing"; its plural is either dessins d'enfant, "child's drawings", or dessins d'enfants, "children's drawings".
In mathematics, the Feit–Thompson theorem, or odd order theorem, states that every finite group of odd order is solvable. It was proved by Walter Feit and John Griggs Thompson.
In mathematics, specifically group theory, Cauchy's theorem states that if G is a finite group and p is a prime number dividing the order of G, then G contains an element of order p. That is, there is x in G such that p is the smallest positive integer with xp = e, where e is the identity element of G. It is named after Augustin-Louis Cauchy, who discovered it in 1845.
In mathematics, a generalized polygon is an incidence structure introduced by Jacques Tits in 1959. Generalized n-gons encompass as special cases projective planes (generalized triangles, n = 3) and generalized quadrangles (n = 4). Many generalized polygons arise from groups of Lie type, but there are also exotic ones that cannot be obtained in this way. Generalized polygons satisfying a technical condition known as the Moufang property have been completely classified by Tits and Weiss. Every generalized n-gon with n even is also a near polygon.
In the mathematical subject of group theory, small cancellation theory studies groups given by group presentations satisfying small cancellation conditions, that is where defining relations have "small overlaps" with each other. Small cancellation conditions imply algebraic, geometric and algorithmic properties of the group. Finitely presented groups satisfying sufficiently strong small cancellation conditions are word hyperbolic and have word problem solvable by Dehn's algorithm. Small cancellation methods are also used for constructing Tarski monsters, and for solutions of Burnside's problem.
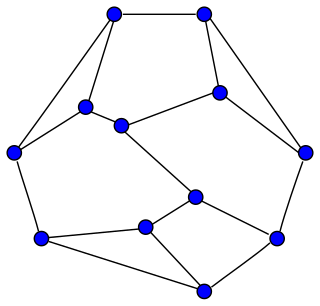
Frucht's theorem is a result in algebraic graph theory, conjectured by Dénes Kőnig in 1936 and proved by Robert Frucht in 1939. It states that every finite group is the group of symmetries of a finite undirected graph. More strongly, for any finite group G there exist infinitely many non-isomorphic simple connected graphs such that the automorphism group of each of them is isomorphic to G.
In mathematics, in the area of abstract algebra, a signalizer functor is a mapping from a potential finite subgroup to the centralizers of the nontrivial elements of an abelian group. The signalizer functor theorem provides the conditions under which the source of such a functor is in fact a subgroup.
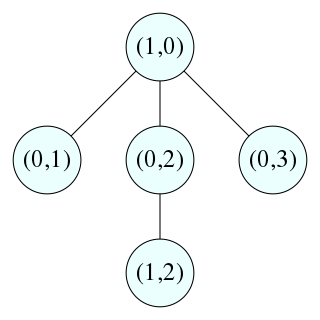
In mathematics, and more specifically in combinatorial commutative algebra, a zero-divisor graph is an undirected graph representing the zero divisors of a commutative ring. It has elements of the ring as its vertices, and pairs of elements whose product is zero as its edges.
Maria Silvia Lucido was an Italian mathematician specializing in group theory, and a researcher in mathematics at the University of Udine.
