In geometry, an n-gonal antiprism or n-antiprism is a polyhedron composed of two parallel direct copies of an n-sided polygon, connected by an alternating band of 2n triangles. They are represented by the Conway notation An.
In geometry, a polyhedral compound is a figure that is composed of several polyhedra sharing a common centre. They are the three-dimensional analogs of polygonal compounds such as the hexagram.
In geometry, a 4-polytope is a four-dimensional polytope. It is a connected and closed figure, composed of lower-dimensional polytopal elements: vertices, edges, faces (polygons), and cells (polyhedra). Each face is shared by exactly two cells. The 4-polytopes were discovered by the Swiss mathematician Ludwig Schläfli before 1853.
In geometry, a prism is a polyhedron comprising an n-sided polygon base, a second base which is a translated copy of the first, and n other faces, necessarily all parallelograms, joining corresponding sides of the two bases. All cross-sections parallel to the bases are translations of the bases. Prisms are named after their bases, e.g. a prism with a pentagonal base is called a pentagonal prism. Prisms are a subclass of prismatoids.
In geometry, the Schläfli symbol is a notation of the form that defines regular polytopes and tessellations.
In geometry, a uniform 4-polytope is a 4-dimensional polytope which is vertex-transitive and whose cells are uniform polyhedra, and faces are regular polygons.
In geometry, a uniform polyhedron has regular polygons as faces and is vertex-transitive—there is an isometry mapping any vertex onto any other. It follows that all vertices are congruent. Uniform polyhedra may be regular, quasi-regular, or semi-regular. The faces and vertices don't need to be convex, so many of the uniform polyhedra are also star polyhedra.
In six-dimensional geometry, a uniform 6-polytope is a six-dimensional uniform polytope. A uniform polypeton is vertex-transitive, and all facets are uniform 5-polytopes.
In geometry, a uniform polytope of dimension three or higher is a vertex-transitive polytope bounded by uniform facets. Here, "vertex-transitive" means that it has symmetries taking every vertex to every other vertex; the same must also be true within each lower-dimensional face of the polytope. In two dimensions a stronger definition is used: only the regular polygons are considered as uniform, disallowing polygons that alternate between two different lengths of edges.
In geometry, a prismatic uniform polyhedron is a uniform polyhedron with dihedral symmetry. They exist in two infinite families, the uniform prisms and the uniform antiprisms. All have their vertices in parallel planes and are therefore prismatoids.
In geometry, a uniform 5-polytope is a five-dimensional uniform polytope. By definition, a uniform 5-polytope is vertex-transitive and constructed from uniform 4-polytope facets.
Each member of this infinite family of uniform polyhedron compounds is a symmetric arrangement of prisms sharing a common axis of rotational symmetry.
In geometry, a prismatic compound of antiprism is a category of uniform polyhedron compound. Each member of this infinite family of uniform polyhedron compounds is a symmetric arrangement of antiprisms sharing a common axis of rotational symmetry.
Each member of this infinite family of uniform polyhedron compounds is a symmetric arrangement of antiprisms sharing a common axis of rotational symmetry. It arises from superimposing two copies of the corresponding prismatic compound of antiprisms, and rotating each copy by an equal and opposite angle.
In hyperbolic geometry, a uniform hyperbolic tiling is an edge-to-edge filling of the hyperbolic plane which has regular polygons as faces and is vertex-transitive. It follows that all vertices are congruent, and the tiling has a high degree of rotational and translational symmetry.
In geometry, a compound of four tetrahedra can be constructed by four tetrahedra in a number of different symmetry positions.
In four-dimensional geometry, a prismatic uniform 4-polytope is a uniform 4-polytope with a nonconnected Coxeter diagram symmetry group. These figures are analogous to the set of prisms and antiprism uniform polyhedra, but add a third category called duoprisms, constructed as a product of two regular polygons.
In the field of hyperbolic geometry, the order-6 hexagonal tiling honeycomb is one of 11 regular paracompact honeycombs in 3-dimensional hyperbolic space. It is paracompact because it has cells with an infinite number of faces. Each cell is a hexagonal tiling whose vertices lie on a horosphere: a flat plane in hyperbolic space that approaches a single ideal point at infinity.
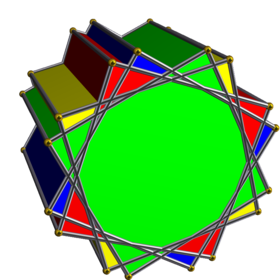(n=2, p=4, q=1)