Kinematics is a subfield of physics, developed in classical mechanics, that describes the motion of points, bodies (objects), and systems of bodies without considering the forces that cause them to move. Kinematics, as a field of study, is often referred to as the "geometry of motion" and is occasionally seen as a branch of mathematics. A kinematics problem begins by describing the geometry of the system and declaring the initial conditions of any known values of position, velocity and/or acceleration of points within the system. Then, using arguments from geometry, the position, velocity and acceleration of any unknown parts of the system can be determined. The study of how forces act on bodies falls within kinetics, not kinematics. For further details, see analytical dynamics.
A projectile is any object thrown by the exertion of a force. It can also be defined as an object launched into the space and allowed to move free under the influence of gravity and air resistance. Although any object in motion through space may be called projectiles, they are commonly found in warfare and sports. Mathematical equations of motion are used to analyze projectile trajectories.

In physics, work is the energy transferred to or from an object via the application of force along a displacement. In its simplest form, it is often represented as the product of force and displacement. A force is said to do positive work if it has a component in the direction of the displacement of the point of application. A force does negative work if it has a component opposite to the direction of the displacement at the point of application of the force.

A geosynchronous transfer orbit or geostationary transfer orbit (GTO) is a type of geocentric orbit. Satellites which are destined for geosynchronous (GSO) or geostationary orbit (GEO) are (almost) always put into a GTO as an intermediate step for reaching their final orbit.

Orbital mechanics or astrodynamics is the application of ballistics and celestial mechanics to the practical problems concerning the motion of rockets and other spacecraft. The motion of these objects is usually calculated from Newton's laws of motion and law of universal gravitation. Orbital mechanics is a core discipline within space-mission design and control.
A guidance system is a virtual or physical device, or a group of devices implementing a controlling the movement of a ship, aircraft, missile, rocket, satellite, or any other moving object. Guidance is the process of calculating the changes in position, velocity, altitude, and/or rotation rates of a moving object required to follow a certain trajectory and/or altitude profile based on information about the object's state of motion.

In the physical science of dynamics, rigid-body dynamics studies the movement of systems of interconnected bodies under the action of external forces. The assumption that the bodies are rigid simplifies analysis, by reducing the parameters that describe the configuration of the system to the translation and rotation of reference frames attached to each body. This excludes bodies that display fluid, highly elastic, and plastic behavior.

In differential geometry, the Frenet–Serret formulas describe the kinematic properties of a particle moving along a continuous, differentiable curve in three-dimensional Euclidean space R3, or the geometric properties of the curve itself irrespective of any motion. More specifically, the formulas describe the derivatives of the so-called tangent, normal, and binormal unit vectors in terms of each other. The formulas are named after the two French mathematicians who independently discovered them: Jean Frédéric Frenet, in his thesis of 1847, and Joseph Alfred Serret in 1851. Vector notation and linear algebra currently used to write these formulas were not yet in use at the time of their discovery.
Verlet integration is a numerical method used to integrate Newton's equations of motion. It is frequently used to calculate trajectories of particles in molecular dynamics simulations and computer graphics. The algorithm was first used in 1791 by Delambre and has been rediscovered many times since then, most recently by Loup Verlet in the 1960s for use in molecular dynamics. It was also used by Cowell and Crommelin in 1909 to compute the orbit of Halley's Comet, and by Carl Størmer in 1907 to study the trajectories of electrical particles in a magnetic field . The Verlet integrator provides good numerical stability, as well as other properties that are important in physical systems such as time reversibility and preservation of the symplectic form on phase space, at no significant additional computational cost over the simple Euler method.

In astrodynamics and celestial dynamics, the orbital state vectors of an orbit are Cartesian vectors of position and velocity that together with their time (epoch) uniquely determine the trajectory of the orbiting body in space.
In spaceflight, an orbital maneuver is the use of propulsion systems to change the orbit of a spacecraft. For spacecraft far from Earth an orbital maneuver is called a deep-space maneuver (DSM).

Screw theory is the algebraic calculation of pairs of vectors, such as forces and moments or angular and linear velocity, that arise in the kinematics and dynamics of rigid bodies. The mathematical framework was developed by Sir Robert Stawell Ball in 1876 for application in kinematics and statics of mechanisms.

Spacecraft flight dynamics is the application of mechanical dynamics to model how the external forces acting on a space vehicle or spacecraft determine its flight path. These forces are primarily of three types: propulsive force provided by the vehicle's engines; gravitational force exerted by the Earth and other celestial bodies; and aerodynamic lift and drag.
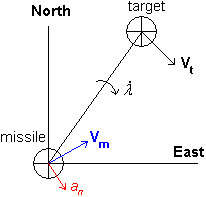
Proportional navigation is a guidance law used in some form or another by most homing air target missiles. It is based on the fact that two vehicles are on a collision course when their direct Line-of-Sight does not change direction as the range closes. PN dictates that the missile velocity vector should rotate at a rate proportional to the rotation rate of the line of sight, and in the same direction.

Space-time adaptive processing (STAP) is a signal processing technique most commonly used in radar systems. It involves adaptive array processing algorithms to aid in target detection. Radar signal processing benefits from STAP in areas where interference is a problem. Through careful application of STAP, it is possible to achieve order-of-magnitude sensitivity improvements in target detection.
A gravity turn or zero-lift turn is a maneuver used in launching a spacecraft into, or descending from, an orbit around a celestial body such as a planet or a moon. It is a trajectory optimization that uses gravity to steer the vehicle onto its desired trajectory. It offers two main advantages over a trajectory controlled solely through the vehicle's own thrust. First, the thrust is not used to change the spacecraft's direction, so more of it is used to accelerate the vehicle into orbit. Second, and more importantly, during the initial ascent phase the vehicle can maintain low or even zero angle of attack. This minimizes transverse aerodynamic stress on the launch vehicle, allowing for a lighter launch vehicle.
Guidance, navigation and control is a branch of engineering dealing with the design of systems to control the movement of vehicles, especially, automobiles, ships, aircraft, and spacecraft. In many cases these functions can be performed by trained humans. However, because of the speed of, for example, a rocket's dynamics, human reaction time is too slow to control this movement. Therefore, systems—now almost exclusively digital electronic—are used for such control. Even in cases where humans can perform these functions, it is often the case that GNC systems provide benefits such as alleviating operator work load, smoothing turbulence, fuel savings, etc. In addition, sophisticated applications of GNC enable automatic or remote control.

An inertial navigation system (INS) is a navigation device that uses a computer, motion sensors (accelerometers) and rotation sensors (gyroscopes) to continuously calculate by dead reckoning the position, the orientation, and the velocity of a moving object without the need for external references. Often the inertial sensors are supplemented by a barometric altimeter and sometimes by magnetic sensors (magnetometers) and/or speed measuring devices. INSs are used on mobile robots and on vehicles such as ships, aircraft, submarines, guided missiles, and spacecraft. Other terms used to refer to inertial navigation systems or closely related devices include inertial guidance system, inertial instrument, inertial measurement unit (IMU) and many other variations. Older INS systems generally used an inertial platform as their mounting point to the vehicle and the terms are sometimes considered synonymous.

In chaos theory and fluid dynamics, chaotic mixing is a process by which flow tracers develop into complex fractals under the action of a fluid flow. The flow is characterized by an exponential growth of fluid filaments. Even very simple flows, such as the blinking vortex, or finitely resolved wind fields can generate exceptionally complex patterns from initially simple tracer fields.
The Monte Carlo method for electron transport is a semiclassical Monte Carlo(MC) approach of modeling semiconductor transport. Assuming the carrier motion consists of free flights interrupted by scattering mechanisms, a computer is utilized to simulate the trajectories of particles as they move across the device under the influence of an electric field using classical mechanics. The scattering events and the duration of particle flight is determined through the use of random numbers.

















