Quantum Hall transitions

Last updated

Quantum Hall transitions are the quantum phase transitions that occur between different robustly quantized electronic phases of the quantum Hall effect. The robust quantization of these electronic phases is due to strong localization of electrons in their disordered, two-dimensional potential. But, at the quantum Hall transition, the electron gas delocalizes as can be observed in the laboratory. This phenomenon is understood in the language of topological field theory. Here, a vacuum angle (or 'theta angle') distinguishes between topologically different sectors in the vacuum. These topological sectors correspond to the robustly quantized phases. The quantum Hall transitions can then be understood by looking at the topological excitations (instantons) that occur between those phases.

Contents

Historical perspective

Just after the first measurements on the quantum Hall effect in 1980, [1] physicists wondered how the strongly localized electrons in the disordered potential were able to delocalize at their phase transitions. At that time, the field theory of Anderson localization didn't yet include a topological angle and hence it predicted that: "for any given amount of disorder, all states in two dimensions are localized". A result that was irreconcilable with the observations on delocalization. [2] Without knowing the solution to this problem, physicists resorted to a semi-classical picture of localized electrons that, given a certain energy, were able to percolate through the disorder. [3] This percolation mechanism was what assumed to delocalize the electrons

As a result of this semi-classical idea, many numerical computations were done based on the percolation picture. [4] On top of the classical percolation phase transition, quantum tunneling was included in computer simulations to calculate the critical exponent of the `semi-classical percolation phase transition'. To compare this result with the measured critical exponent, the Fermi-liquid approximation was used, where the Coulomb interactions between electrons are assumed to be finite. Under this assumption, the ground state of the free electron gas can be adiabatically transformed into the ground state of the interacting system and this gives rise to an inelastic scattering length so that the canonical correlation length exponent can be compared to the measured critical exponent.

But, at the quantum phase transition, the localization lengths of the electrons becomes infinite (i.e. they delocalize) and this compromises the Fermi-liquid assumption of an inherently free electron gas (where individual electrons must be well-distinguished). The quantum Hall transition will therefore not be in the Fermi-liquid universality class, but in the 'F-invariant' universality class that has a different value for the critical exponent. [5] The semi-classical percolation picture of the quantum Hall transition is therefore outdated (although still widely used) and we need to understand the delocalization mechanism as an instanton effect.

Disorder in the sample

The random disorder in the potential landscape of the two-dimensional electron gas plays a key role in the observation of topological sectors and their instantons (phase transitions). Because of the disorder, the electrons are localized and thus they cannot flow across the sample. But if we consider a loop around a localized 2D electron, we can notice that current is still able to flow in the direction around this loop. This current is able to renormalize to larger scales and eventually becomes the Hall current that rotates along the edge of the sample. A topological sector corresponds to an integer number of rotations and it is now visible macroscopically, in the robustly quantized behavior of the measurable Hall current. If the electrons were not sufficiently localized, this measurement would be blurred out by the usual flow of current through the sample.

For the subtle observations on phase transitions it is important that the disorder is of the right kind. The random nature of the potential landscape should be apparent on a scale sufficiently smaller than the sample size in order to clearly distinguish the different phases of the system. These phases are only observable by the principle of emergence, so the difference between self-similar scales has to be multiple orders of magnitude for the critical exponent to be well-defined. On the opposite side, when the disorder correlation length is too small, the states are not sufficiently localized to observe them delocalize.

Renormalization group flow diagram

Scaling of the longitudinal and Hall conductivities in a renormalization group flow-diagram of the quantum Hall effect Three Dimensional RG Flowdiagram of the QHE.png
Scaling of the longitudinal and Hall conductivities in a renormalization group flow-diagram of the quantum Hall effect

On the basis of the Renormalization Group Theory of the instanton vacuum one can form a general flow diagram where the topological sectors are represented by attractive fixed points. When scaling the effective system to larger sizes, the system generally flows to a stable phase at one of these points and as we can see in the flow diagram on the right, the longitudinal conductivity will vanish and the Hall conductivity takes on a quantized value. If we started with a Hall conductivity that is halfway between two attractive points, we would end up on the phase transition between topological sectors. As long as the symmetry isn't broken, the longitudinal conductivity doesn't vanish and is even able to increase when scaling to a larger system size. In the flow diagram, we see fixed points that are repulsive in the direction of the Hall current and attractive in the direction of the longitudinal current. It is most interesting to approach these fixed saddle points as close as possible and measure the (universal) behavior of the quantum Hall transitions.

Super-universality

If the system is rescaled, the change in conductivity depends only on the distance between a fixed saddle point and the conductivity. The scaling behavior near the quantum Hall transitions is then universal and different quantum Hall samples will give the same scaling results. But, by studying the quantum Hall transitions theoretically, many different systems that are all in different universality classes have been found to share a super-universal fixed point structure. [6] This means that many different systems that are all in different universality classes still share the same fixed point structure. They all have stable topological sectors and also share other super-universal features. That these features are super-universal is due to the fundamental nature of the vacuum angle that governs the scaling behavior of the systems. The topological vacuum angle can be constructed in any quantum field theory but only under the right circumstances can its features be observed. The vacuum angle also appears in quantum chromodynamics and might have been important in the formation of the early universe.

See also

Related Research Articles

<span class="mw-page-title-main">Condensed matter physics</span> Branch of physics

Condensed matter physics is the field of physics that deals with the macroscopic and microscopic physical properties of matter, especially the solid and liquid phases that arise from electromagnetic forces between atoms and electrons. More generally, the subject deals with condensed phases of matter: systems of many constituents with strong interactions among them. More exotic condensed phases include the superconducting phase exhibited by certain materials at extremely low cryogenic temperatures, the ferromagnetic and antiferromagnetic phases of spins on crystal lattices of atoms, the Bose–Einstein condensates found in ultracold atomic systems, and liquid crystals. Condensed matter physicists seek to understand the behavior of these phases by experiments to measure various material properties, and by applying the physical laws of quantum mechanics, electromagnetism, statistical mechanics, and other physics theories to develop mathematical models and predict the properties of extremely large groups of atoms.

<span class="mw-page-title-main">Metallic bonding</span> Type of chemical bond in metals

Metallic bonding is a type of chemical bonding that arises from the electrostatic attractive force between conduction electrons and positively charged metal ions. It may be described as the sharing of free electrons among a structure of positively charged ions (cations). Metallic bonding accounts for many physical properties of metals, such as strength, ductility, thermal and electrical resistivity and conductivity, opacity, and lustre.

The quantum Hall effect is a quantized version of the Hall effect which is observed in two-dimensional electron systems subjected to low temperatures and strong magnetic fields, in which the Hall resistance Rxy exhibits steps that take on the quantized values

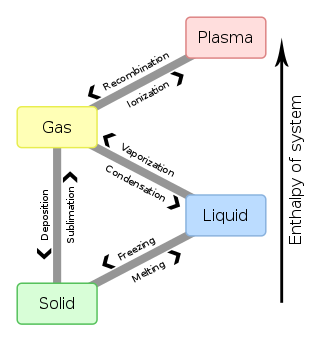
<span class="mw-page-title-main">Phase transition</span> Physical process of transition between basic states of matter

In chemistry, thermodynamics, and other related fields like physics and biology, a phase transition is the physical process of transition between one state of a medium and another. Commonly the term is used to refer to changes among the basic states of matter: solid, liquid, and gas, and in rare cases, plasma. A phase of a thermodynamic system and the states of matter have uniform physical properties. During a phase transition of a given medium, certain properties of the medium change as a result of the change of external conditions, such as temperature or pressure. This can be a discontinuous change; for example, a liquid may become gas upon heating to its boiling point, resulting in an abrupt change in volume. The identification of the external conditions at which a transformation occurs defines the phase transition point.

<span class="mw-page-title-main">Fermi level</span> Quantity in solid state thermodynamics

The Fermi level of a solid-state body is the thermodynamic work required to add one electron to the body. It is a thermodynamic quantity usually denoted by µ or EF for brevity. The Fermi level does not include the work required to remove the electron from wherever it came from. A precise understanding of the Fermi level—how it relates to electronic band structure in determining electronic properties; how it relates to the voltage and flow of charge in an electronic circuit—is essential to an understanding of solid-state physics.

<span class="mw-page-title-main">Fermi liquid theory</span> Theoretical model in physics

Fermi liquid theory is a theoretical model of interacting fermions that describes the normal state of the conduction electrons in most metals at sufficiently low temperatures. The theory describes the behavior of many-body systems of particles in which the interactions between particles may be strong. The phenomenological theory of Fermi liquids was introduced by the Soviet physicist Lev Davidovich Landau in 1956, and later developed by Alexei Abrikosov and Isaak Khalatnikov using diagrammatic perturbation theory. The theory explains why some of the properties of an interacting fermion system are very similar to those of the ideal Fermi gas, and why other properties differ.

In theoretical physics, the term renormalization group (RG) refers to a formal apparatus that allows systematic investigation of the changes of a physical system as viewed at different scales. In particle physics, it reflects the changes in the underlying force laws as the energy scale at which physical processes occur varies, energy/momentum and resolution distance scales being effectively conjugate under the uncertainty principle.

In physics, critical phenomena is the collective name associated with the physics of critical points. Most of them stem from the divergence of the correlation length, but also the dynamics slows down. Critical phenomena include scaling relations among different quantities, power-law divergences of some quantities described by critical exponents, universality, fractal behaviour, and ergodicity breaking. Critical phenomena take place in second order phase transitions, although not exclusively.

In physics, a quantum phase transition (QPT) is a phase transition between different quantum phases. Contrary to classical phase transitions, quantum phase transitions can only be accessed by varying a physical parameter—such as magnetic field or pressure—at absolute zero temperature. The transition describes an abrupt change in the ground state of a many-body system due to its quantum fluctuations. Such a quantum phase transition can be a second-order phase transition. Quantum phase transitions can also be represented by the topological fermion condensation quantum phase transition, see e.g. strongly correlated quantum spin liquid. In case of three dimensional Fermi liquid, this transition transforms the Fermi surface into a Fermi volume. Such a transition can be a first-order phase transition, for it transforms two dimensional structure into three dimensional. As a result, the topological charge of Fermi liquid changes abruptly, since it takes only one of a discrete set of values.

In physics, mathematics and statistics, scale invariance is a feature of objects or laws that do not change if scales of length, energy, or other variables, are multiplied by a common factor, and thus represent a universality.

In quantum field theory, a nonlinear σ model describes a scalar field Σ which takes on values in a nonlinear manifold called the target manifold T. The non-linear σ-model was introduced by Gell-Mann & Lévy, who named it after a field corresponding to a spinless meson called σ in their model. This article deals primarily with the quantization of the non-linear sigma model; please refer to the base article on the sigma model for general definitions and classical (non-quantum) formulations and results.

In statistical mechanics, universality is the observation that there are properties for a large class of systems that are independent of the dynamical details of the system. Systems display universality in a scaling limit, when a large number of interacting parts come together. The modern meaning of the term was introduced by Leo Kadanoff in the 1960s, but a simpler version of the concept was already implicit in the van der Waals equation and in the earlier Landau theory of phase transitions, which did not incorporate scaling correctly.

The QCD vacuum is the quantum vacuum state of quantum chromodynamics (QCD). It is an example of a non-perturbative vacuum state, characterized by non-vanishing condensates such as the gluon condensate and the quark condensate in the complete theory which includes quarks. The presence of these condensates characterizes the confined phase of quark matter.

Critical exponents describe the behavior of physical quantities near continuous phase transitions. It is believed, though not proven, that they are universal, i.e. they do not depend on the details of the physical system, but only on some of its general features. For instance, for ferromagnetic systems, the critical exponents depend only on:

<span class="mw-page-title-main">Topological order</span> Type of order at absolute zero

In physics, topological order is a kind of order in the zero-temperature phase of matter. Macroscopically, topological order is defined and described by robust ground state degeneracy and quantized non-Abelian geometric phases of degenerate ground states. Microscopically, topological orders correspond to patterns of long-range quantum entanglement. States with different topological orders cannot change into each other without a phase transition.

The superconductor–insulator transition is an example of a quantum phase transition, whereupon tuning some parameter in the Hamiltonian, a dramatic change in the behavior of the electrons occurs. The nature of how this transition occurs is disputed, and many studies seek to understand how the order parameter, , changes. Here is the amplitude of the order parameter, and is the phase. Most theories involve either the destruction of the amplitude of the order parameter - by a reduction in the density of states at the Fermi surface, or by destruction of the phase coherence; which results from the proliferation of vortices.

In Materials Science, heavy fermion materials are a specific type of intermetallic compound, containing elements with 4f or 5f electrons in unfilled electron bands. Electrons are one type of fermion, and when they are found in such materials, they are sometimes referred to as heavy electrons. Heavy fermion materials have a low-temperature specific heat whose linear term is up to 1000 times larger than the value expected from the free electron model. The properties of the heavy fermion compounds often derive from the partly filled f-orbitals of rare-earth or actinide ions, which behave like localized magnetic moments.

In theoretical physics, functional renormalization group (FRG) is an implementation of the renormalization group (RG) concept which is used in quantum and statistical field theory, especially when dealing with strongly interacting systems. The method combines functional methods of quantum field theory with the intuitive renormalization group idea of Kenneth G. Wilson. This technique allows to interpolate smoothly between the known microscopic laws and the complicated macroscopic phenomena in physical systems. In this sense, it bridges the transition from simplicity of microphysics to complexity of macrophysics. Figuratively speaking, FRG acts as a microscope with a variable resolution. One starts with a high-resolution picture of the known microphysical laws and subsequently decreases the resolution to obtain a coarse-grained picture of macroscopic collective phenomena. The method is nonperturbative, meaning that it does not rely on an expansion in a small coupling constant. Mathematically, FRG is based on an exact functional differential equation for a scale-dependent effective action.

In theoretical physics, the curvature renormalization group (CRG) method is an analytical approach to determine the phase boundaries and the critical behavior of topological systems. Topological phases are phases of matter that appear in certain quantum mechanical systems at zero temperature because of a robust degeneracy in the ground-state wave function. They are called topological because they can be described by different (discrete) values of a nonlocal topological invariant. This is to contrast with non-topological phases of matter that can be described by different values of a local order parameter. States with different values of the topological invariant cannot change into each other without a phase transition. The topological invariant is constructed from a curvature function that can be calculated from the bulk Hamiltonian of the system. At the phase transition, the curvature function diverges, and the topological invariant correspondingly jumps abruptly from one value to another. The CRG method works by detecting the divergence in the curvature function, and thus determining the boundaries between different topological phases. Furthermore, from the divergence of the curvature function, it extracts scaling laws that describe the critical behavior, i.e. how different quantities behave as the topological phase transition is approached. The CRG method has been successfully applied to a variety of static, periodically driven, weakly and strongly interacting systems to classify the nature of the corresponding topological phase transitions.

References

  1. ↑ Klitzing, K. v.; Dorda, G.; Pepper, M. (11 August 1980). "New Method for High-Accuracy Determination of the Fine-Structure Constant Based on Quantized Hall Resistance". Physical Review Letters. 45 (6). American Physical Society (APS): 494–497. Bibcode:1980PhRvL..45..494K. doi: 10.1103/physrevlett.45.494 . ISSN   0031-9007.
  2. ↑ Wei, H. P.; Tsui, D. C.; Pruisken, A. M. M. (15 January 1986). "Localization and scaling in the quantum Hall regime". Physical Review B. 33 (2). American Physical Society (APS): 1488–1491. Bibcode:1986PhRvB..33.1488W. doi:10.1103/physrevb.33.1488. ISSN   0163-1829. PMID   9938439.
  3. ↑ Kazarinov, R. F.; Luryi, Serge (15 June 1982). "Quantum percolation and quantization of Hall resistance in two-dimensional electron gas". Physical Review B. 25 (12). American Physical Society (APS): 7626–7630. Bibcode:1982PhRvB..25.7626K. doi:10.1103/physrevb.25.7626. ISSN   0163-1829.
  4. ↑ Chalker, J T; Coddington, P D (20 May 1988). "Percolation, quantum tunnelling and the integer Hall effect". Journal of Physics C: Solid State Physics. 21 (14). IOP Publishing: 2665–2679. Bibcode:1988JPhC...21.2665C. doi:10.1088/0022-3719/21/14/008. ISSN   0022-3719.
  5. ↑ Pruisken, A.M.M.; Burmistrov, I.S. (2007). "θ renormalization, electron–electron interactions and super universality in the quantum Hall regime". Annals of Physics. 322 (6). Elsevier BV: 1265–1334. arXiv: cond-mat/0502488 . Bibcode:2007AnPhy.322.1265P. doi:10.1016/j.aop.2006.11.007. ISSN   0003-4916. S2CID   119376597.
  6. ↑ Pruisken, A.M.M. (2009). "Super universality of the quantum Hall effect and the "large N picture" of the theta angle". International Journal of Theoretical Physics. 48 (6): 1736–1765. arXiv: 0811.3299 . Bibcode:2009IJTP...48.1736P. doi:10.1007/s10773-009-9947-7. S2CID   13874231.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.