The Ragsdale conjecture is a mathematical conjecture that concerns the possible arrangements of real algebraic curves embedded in the projective plane. It was proposed by Virginia Ragsdale in her dissertation in 1906 and was disproved in 1979. It has been called "the oldest and most famous conjecture on the topology of real algebraic curves". [1]
Ragsdale's dissertation, "On the Arrangement of the Real Branches of Plane Algebraic Curves," was published by the American Journal of Mathematics in 1906. The dissertation was a treatment of Hilbert's sixteenth problem, which had been proposed by Hilbert in 1900, along with 22 other unsolved problems of the 19th century; it is one of the handful of Hilbert's problems that remains wholly unresolved. Ragsdale formulated a conjecture that provided an upper bound on the number of topological circles of a certain type, [2] along with the basis of evidence.
Ragsdale's main conjecture is as follows.
Assume that an algebraic curve of degree 2k contains p even and n odd ovals. Ragsdale conjectured that
She also posed the inequality
and showed that the inequality could not be further improved. This inequality was later proved by Petrovsky.
The conjecture was held of very high importance in the field of real algebraic geometry for most of the twentieth century. Later, in 1980, Oleg Viro [3] introduced a technique known as "patchworking algebraic curves" [1] and used to generate a counterexample to the conjecture.
In 1993, Ilia Itenberg [4] produced additional counterexamples to the Ragsdale conjecture, so Viro and Itenberg wrote a paper in 1996 discussing their work on disproving the conjecture using the "patchworking" technique. [1]
The problem of finding a sharp upper bound remains unsolved.
In mathematics, a conjecture is a conclusion or a proposition which is suspected to be true due to preliminary supporting evidence, but for which no proof or disproof has yet been found. Some conjectures, such as the Riemann hypothesis or Fermat's Last Theorem, have shaped much of mathematical history as new areas of mathematics are developed in order to prove them.
The abc conjecture is a conjecture in number theory, first proposed by Joseph Oesterlé (1988) and David Masser (1985). It is stated in terms of three positive integers, a, b and c that are relatively prime and satisfy a + b = c. If d denotes the product of the distinct prime factors of abc, the conjecture essentially states that d is usually not much smaller than c. In other words: if a and b are composed from large powers of primes, then c is usually not divisible by large powers of primes. A number of famous conjectures and theorems in number theory would follow immediately from the abc conjecture or its versions. Goldfeld (1996) described the abc conjecture as "the most important unsolved problem in Diophantine analysis".
In mathematics, the Hodge conjecture is a major unsolved problem in algebraic geometry that relates the algebraic topology of a non-singular complex algebraic variety to its subvarieties. More specifically, the conjecture states that certain de Rham cohomology classes are algebraic; that is, they are sums of Poincaré duals of the homology classes of subvarieties. It was formulated by the Scottish mathematician William Vallance Douglas Hodge as a result of a work in between 1930 and 1940 to enrich the description of de Rham cohomology to include extra structure that is present in the case of complex algebraic varieties. It received little attention before Hodge presented it in an address during the 1950 International Congress of Mathematicians, held in Cambridge, Massachusetts. The Hodge conjecture is one of the Clay Mathematics Institute's Millennium Prize Problems, with a prize of $1,000,000 for whoever can prove or disprove the Hodge conjecture.
In mathematics, the Mertens conjecture is the statement that the Mertens function is bounded by . Although now disproven, it has been shown to imply the Riemann hypothesis. It was conjectured by Thomas Joannes Stieltjes, in an 1885 letter to Charles Hermite, and again in print by Franz Mertens (1897), and disproved by Andrew Odlyzko and Herman te Riele (1985). It is a striking example of a mathematical conjecture proven false despite a large amount of computational evidence in its favor.
In mathematics, Diophantine geometry is the study of points of algebraic varieties with coordinates in the integers, rational numbers, and their generalizations. These generalizations typically are fields that are not algebraically closed, such as number fields, finite fields, function fields, and p-adic fields. It is a sub-branch of arithmetic geometry and is one approach to the theory of Diophantine equations, formulating questions about such equations in terms of algebraic geometry.
In mathematics, Hilbert's fourteenth problem, that is, number 14 of Hilbert's problems proposed in 1900, asks whether certain algebras are finitely generated.
Hilbert's seventeenth problem is one of the 23 Hilbert problems set out in a celebrated list compiled in 1900 by David Hilbert. It concerns the expression of positive definite rational functions as sums of quotients of squares. The original question may be reformulated as:
In mathematics, Clifford's theorem on special divisors is a result of William K. Clifford (1878) on algebraic curves, showing the constraints on special linear systems on a curve C.
In mathematics, a Kloosterman sum is a particular kind of exponential sum. They are named for the Dutch mathematician Hendrik Kloosterman, who introduced them in 1926 when he adapted the Hardy–Littlewood circle method to tackle a problem involving positive definite diagonal quadratic forms in four as opposed to five or more variables, which he had dealt with in his dissertation in 1924.
Masayoshi Nagata was a Japanese mathematician, known for his work in the field of commutative algebra.
A height function is a function that quantifies the complexity of mathematical objects. In Diophantine geometry, height functions quantify the size of solutions to Diophantine equations and are typically functions from a set of points on algebraic varieties to the real numbers.
In number theory, the Pólya conjecture stated that "most" of the natural numbers less than any given number have an odd number of prime factors. The conjecture was posited by the Hungarian mathematician George Pólya in 1919, and proved false in 1958 by C. Brian Haselgrove.
In mathematics, the Nagata conjecture on curves, named after Masayoshi Nagata, governs the minimal degree required for a plane algebraic curve to pass through a collection of very general points with prescribed multiplicities.
In mathematics, real algebraic geometry is the sub-branch of algebraic geometry studying real algebraic sets, i.e. real-number solutions to algebraic equations with real-number coefficients, and mappings between them.
Ganea's conjecture is a claim in algebraic topology, now disproved. It states that
In mathematics, the Golod–Shafarevich theorem was proved in 1964 by Evgeny Golod and Igor Shafarevich. It is a result in non-commutative homological algebra which solves the class field tower problem, by showing that class field towers can be infinite.
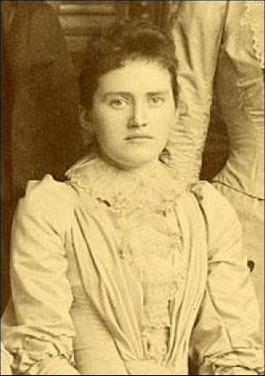
Virginia Ragsdale was a teacher and a mathematician specializing in algebraic curves. She is most known as the creator of the Ragsdale conjecture.
Oleg Yanovich Viro is a Russian mathematician in the fields of topology and algebraic geometry, most notably real algebraic geometry, tropical geometry and knot theory.
In operator theory, von Neumann's inequality, due to John von Neumann, states that, for a fixed contraction T, the polynomial functional calculus map is itself a contraction.
