External links
-
 Media related to Random tree at Wikimedia Commons
Media related to Random tree at Wikimedia Commons
| Part of a series on |
| Probabilistic data structures |
|---|
| Random trees |
| Related |
In mathematics and computer science, a random tree is a tree or arborescence that is formed by a stochastic process. Types of random trees include:

In computer science, a search algorithm is an algorithm designed to solve a search problem. Search algorithms work to retrieve information stored within particular data structure, or calculated in the search space of a problem domain, with either discrete or continuous values.

A minimum spanning tree (MST) or minimum weight spanning tree is a subset of the edges of a connected, edge-weighted undirected graph that connects all the vertices together, without any cycles and with the minimum possible total edge weight. That is, it is a spanning tree whose sum of edge weights is as small as possible. More generally, any edge-weighted undirected graph has a minimum spanning forest, which is a union of the minimum spanning trees for its connected components.

Dijkstra's algorithm is an algorithm for finding the shortest paths between nodes in a weighted graph, which may represent, for example, road networks. It was conceived by computer scientist Edsger W. Dijkstra in 1956 and published three years later.

Kruskal's algorithm finds a minimum spanning forest of an undirected edge-weighted graph. If the graph is connected, it finds a minimum spanning tree. It is a greedy algorithm that in each step adds to the forest the lowest-weight edge that will not form a cycle. The key steps of the algorithm are sorting and the use of a disjoint-set data structure to detect cycles. Its running time is dominated by the time to sort all of the graph edges by their weight.

In computer science, Prim's algorithm is a greedy algorithm that finds a minimum spanning tree for a weighted undirected graph. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized. The algorithm operates by building this tree one vertex at a time, from an arbitrary starting vertex, at each step adding the cheapest possible connection from the tree to another vertex.

Depth-first search (DFS) is an algorithm for traversing or searching tree or graph data structures. The algorithm starts at the root node and explores as far as possible along each branch before backtracking. Extra memory, usually a stack, is needed to keep track of the nodes discovered so far along a specified branch which helps in backtracking of the graph.
Maze generation algorithms are automated methods for the creation of mazes.

In mathematics, a random walk, sometimes known as a drunkard's walk, is a random process that describes a path that consists of a succession of random steps on some mathematical space.
This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.

In mathematics, random graph is the general term to refer to probability distributions over graphs. Random graphs may be described simply by a probability distribution, or by a random process which generates them. The theory of random graphs lies at the intersection between graph theory and probability theory. From a mathematical perspective, random graphs are used to answer questions about the properties of typical graphs. Its practical applications are found in all areas in which complex networks need to be modeled – many random graph models are thus known, mirroring the diverse types of complex networks encountered in different areas. In a mathematical context, random graph refers almost exclusively to the Erdős–Rényi random graph model. In other contexts, any graph model may be referred to as a random graph.

In the mathematical field of graph theory, a spanning treeT of an undirected graph G is a subgraph that is a tree which includes all of the vertices of G. In general, a graph may have several spanning trees, but a graph that is not connected will not contain a spanning tree. If all of the edges of G are also edges of a spanning tree T of G, then G is a tree and is identical to T.

A Euclidean minimum spanning tree of a finite set of points in the Euclidean plane or higher-dimensional Euclidean space connects the points by a system of line segments with the points as endpoints, minimizing the total length of the segments. In it, any two points can reach each other along a path through the line segments. It can be found as the minimum spanning tree of a complete graph with the points as vertices and the Euclidean distances between points as edge weights.

In mathematics, loop-erased random walk is a model for a random simple path with important applications in combinatorics, physics and quantum field theory. It is intimately connected to the uniform spanning tree, a model for a random tree. See also random walk for more general treatment of this topic.

A spatial network is a graph in which the vertices or edges are spatial elements associated with geometric objects, i.e., the nodes are located in a space equipped with a certain metric. The simplest mathematical realization of spatial network is a lattice or a random geometric graph, where nodes are distributed uniformly at random over a two-dimensional plane; a pair of nodes are connected if the Euclidean distance is smaller than a given neighborhood radius. Transportation and mobility networks, Internet, mobile phone networks, power grids, social and contact networks and biological neural networks are all examples where the underlying space is relevant and where the graph's topology alone does not contain all the information. Characterizing and understanding the structure, resilience and the evolution of spatial networks is crucial for many different fields ranging from urbanism to epidemiology.

In computer science, a Cartesian tree is a binary tree derived from a sequence of distinct numbers. To construct the Cartesian tree, set its root to be the minimum number in the sequence, and recursively construct its left and right subtrees from the subsequences before and after this number. It is uniquely defined as a min-heap whose symmetric (in-order) traversal returns the original sequence.
Order in mathematics may refer to:
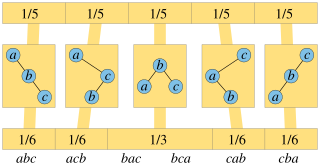
In computer science and probability theory, a random binary tree is a binary tree selected at random from some probability distribution on binary trees. Different distributions have been used, leading to different properties for these trees.