In computer science, a range minimum query (RMQ) solves the problem of finding the minimal value in a sub-array of an array of comparable objects. Range minimum queries have several use cases in computer science, such as the lowest common ancestor problem and the longest common prefix problem (LCP).
Given an array A[1 … n] of n objects taken from a totally ordered set, such as integers, the range minimum query RMQA(l,r) =arg min A[k] (with 1 ≤ l ≤ k ≤ r ≤ n) returns the position of the minimal element in the specified sub-array A[l … r].
For example, when A = [0,5,2,5,4,3,1,6,3], then the answer to the range minimum query for the sub-array A[3 … 8] = [2,5,4,3,1,6] is 7, as A[7] = 1.
In a typical setting, the array A is static, i.e., elements are not inserted or deleted during a series of queries, and the queries to be answered on-line (i.e., the whole set of queries are not known in advance to the algorithm). In this case a suitable preprocessing of the array into a data structure ensures faster query answering. A naive solution is to precompute all possible queries, i.e. the minimum of all sub-arrays of A, and store these in an array B such that B[i, j] = min(A[i…j]); then a range min query can be solved in constant time by array lookup in B. There are Θ(n²) possible queries for a length-n array, and the answers to these can be computed in Θ(n²) time by dynamic programming. [1]
As in the solution above, answering queries in constant time will be achieved by pre-computing results. However, the array will store pre-computed range minimum queries not for every range [i, j], but only for ranges whose size is a power of two. There are O(log n) such queries for each start position i, so the size of the dynamic programming table B is O(n log n). The value of B[i, j] is the index of the minimum of the range A[i…i+2j-1]. Filling the table takes time O(n log n), with the indices of minima using the following recurrence [1] [2]
After this pre-computing step, a query RMQA(l,r) can now be answered in constant time by splitting it into two separate queries: one is the pre-computed query with range from l to the largest memoized value smaller than r. The other is the query of an interval of the same length that has r as its right boundary. These intervals may overlap, but since we are trying to compute the minimum rather than, for example, the sum of the numbers in the array, this does not matter. The overall result can thus be obtained, after the linearithmic time pre-computing, in constant time: the two queries can be answered in constant time and the only thing left to do is to choose the smaller of the two results.
| k | |||||
|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | ||
| l | 1 | 1 | 1 | 1 | 1 |
| 2 | 2 | 3 | 3 | 7 | |
| 3 | 3 | 3 | 3 | 7 | |
| 4 | 4 | 5 | 6 | 7 | |
| 5 | 5 | 6 | 7 | 7 | |
| 6 | 6 | 7 | 7 | 7 | |
| 7 | 7 | 7 | 7 | 7 | |
| 8 | 8 | 7 | 7 | 7 | |
| 9 | 9 | 7 | 7 | 7 | |
This solution does pre-computation in O(n) time. Its data structures use O(n) space and its data structures can be used to answer queries in logarithmic time. [2] The array is first conceptually divided into blocks of size s = log n/4. Then the minimum for each block can be computed in O(n) time overall and the minima are stored in a new array.
RMQs can now be answered in logarithmic time by looking at the blocks containing the left query boundary, the right query boundary and all the blocks in between:
For example, using the array A = [0,5,2,5,4,3,1,6,3] and a block size of 3 (for illustrative purposes only) yields the minimum array A' = [0,3,1].
Using the solution above, the sub-queries inside the blocks that are not fully contained in the query still need to be answered in constant time. There are at most two of those blocks: the block containing l and the block containing r. Constant time is achieved by storing the Cartesian trees for all the blocks in the array. A few observations:
For every such tree, the possible result for all queries need to be stored. This comes down to s2 or O(log2n) entries. This means the overall size of the table is O(n).
To look up results efficiently, the Cartesian tree (row) corresponding to a specific block must be addressable in constant time. The solution is to store the results for all trees in an array and find a unique projection from binary trees to integers to address the entries. This can be achieved by doing a breadth-first-search through the tree and adding leaf nodes so that every existing node in the Cartesian tree has exactly two children. The integer is then generated by representing every inner node as a 0-bit and every leaf as a 1-bit in a bit-word (by traversing the tree in level-order again). This leads to a size of log n/4 for every tree. To enable random access in constant time to any tree, the trees not contained in the original array need to be included as well. An array with indices of log n/4 bits length has size 2log n/4 = O(n).
![Example of Cartesian trees for A = [0,5,2,5,4,3,1,6,3]. Notice that the first and third tree have the same layout, so there are exactly two pre-computed sets of queries in the table on the left. Example of Cartesian Trees.png](http://upload.wikimedia.org/wikipedia/commons/thumb/6/69/Example_of_Cartesian_Trees.png/220px-Example_of_Cartesian_Trees.png)
| Index | 1 | 2 | 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | |
| 0 | — | ||||||||
| 23 (Bitword 0010111) | 1 | 2 | 3 | — | 2 | 3 | — | — | 3 |
| 39 (Bitword 0100111) | 1 | 1 | 1 | — | 2 | 3 | — | — | 3 |
| 127 | — | ||||||||
RMQs are used as a tool for many tasks in exact and approximate string matching. Several applications can be found in Fischer and Heun (2007). [3] : 3
RMQs can be used to solve the lowest common ancestor problem [1] [2] and are used as a tool for many tasks in exact and approximate string matching. The LCA query LCAS(v, w) of a rooted tree S = (V, E) and two nodes v, w ∈ V returns the deepest node u (which may be v or w) on paths from the root to both w and v. Gabow, Bentley, and Tarjan (1984) showed that the LCA Problem can be reduced in linear time to the RMQ problem. It follows that, like the RMQ problem, the LCA problem can be solved in constant time and linear space. [3]
In the context of text indexing, RMQs can be used to find the LCP (longest common prefix), where LCPT(i, j) computes the LCP of the suffixes that start at indexes i and j in T. To do this we first compute the suffix array A, and the inverse suffix array A−1. We then compute the LCP array H giving the LCP of adjacent suffixes in A. Once these data structures are computed, and RMQ preprocessing is complete, the length of the general LCP can be computed in constant time by the formula: LCP(i, j) = RMQH(A-1[i] + 1, A-1[j]), where we assume for simplicity that A-1[i] + 1 <= A-1[j] (otherwise swap). [4]
In computer science, binary search, also known as half-interval search, logarithmic search, or binary chop, is a search algorithm that finds the position of a target value within a sorted array. Binary search compares the target value to the middle element of the array. If they are not equal, the half in which the target cannot lie is eliminated and the search continues on the remaining half, again taking the middle element to compare to the target value, and repeating this until the target value is found. If the search ends with the remaining half being empty, the target is not in the array.
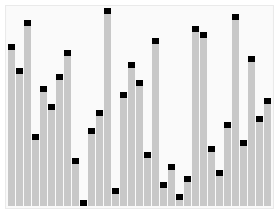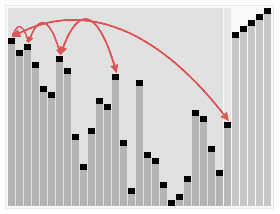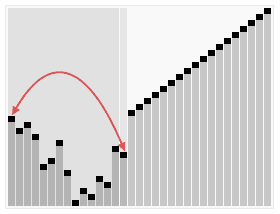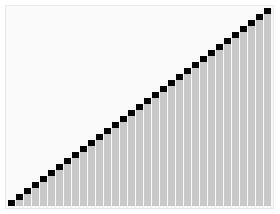
In computer science, heapsort is a comparison-based sorting algorithm which can be thought of as "an implementation of selection sort using the right data structure." Like selection sort, heapsort divides its input into a sorted and an unsorted region, and it iteratively shrinks the unsorted region by extracting the largest element from it and inserting it into the sorted region. Unlike selection sort, heapsort does not waste time with a linear-time scan of the unsorted region; rather, heap sort maintains the unsorted region in a heap data structure to efficiently find the largest element in each step.
In computer science, a suffix tree is a compressed trie containing all the suffixes of the given text as their keys and positions in the text as their values. Suffix trees allow particularly fast implementations of many important string operations.
In computer science, a disjoint-set data structure, also called a union–find data structure or merge–find set, is a data structure that stores a collection of disjoint (non-overlapping) sets. Equivalently, it stores a partition of a set into disjoint subsets. It provides operations for adding new sets, merging sets, and finding a representative member of a set. The last operation makes it possible to find out efficiently if any two elements are in the same or different sets.
In computer science, a fusion tree is a type of tree data structure that implements an associative array on w-bit integers on a finite universe, where each of the input integers has size less than 2w and is non-negative. When operating on a collection of n key–value pairs, it uses O(n) space and performs searches in O(logwn) time, which is asymptotically faster than a traditional self-balancing binary search tree, and also better than the van Emde Boas tree for large values of w. It achieves this speed by using certain constant-time operations that can be done on a machine word. Fusion trees were invented in 1990 by Michael Fredman and Dan Willard.
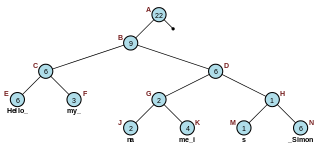
In computer programming, a rope, or cord, is a data structure composed of smaller strings that is used to efficiently store and manipulate a very long string. For example, a text editing program may use a rope to represent the text being edited, so that operations such as insertion, deletion, and random access can be done efficiently.
In computer science, a suffix array is a sorted array of all suffixes of a string. It is a data structure used in, among others, full-text indices, data-compression algorithms, and the field of bibliometrics.
A B+ tree is an m-ary tree with a variable but often large number of children per node. A B+ tree consists of a root, internal nodes and leaves. The root may be either a leaf or a node with two or more children.
In graph theory and computer science, the lowest common ancestor (LCA) of two nodes v and w in a tree or directed acyclic graph (DAG) T is the lowest node that has both v and w as descendants, where we define each node to be a descendant of itself.
In computer science, a succinct data structure is a data structure which uses an amount of space that is "close" to the information-theoretic lower bound, but still allows for efficient query operations. The concept was originally introduced by Jacobson to encode bit vectors, (unlabeled) trees, and planar graphs. Unlike general lossless data compression algorithms, succinct data structures retain the ability to use them in-place, without decompressing them first. A related notion is that of a compressed data structure, insofar as the size of the stored or encoded data similarly depends upon the specific content of the data itself.
In computer science, a Cartesian tree is a binary tree derived from a sequence of distinct numbers. To construct the Cartesian tree, set its root to be the minimum number in the sequence, and recursively construct its left and right subtrees from the subsequences before and after this number. It is uniquely defined as a min-heap whose symmetric (in-order) traversal returns the original sequence.
In computer science, the all nearest smaller values problem is the following task: for each position in a sequence of numbers, search among the previous positions for the last position that contains a smaller value. This problem can be solved efficiently both by parallel and non-parallel algorithms: Berkman, Schieber & Vishkin (1993), who first identified the procedure as a useful subroutine for other parallel programs, developed efficient algorithms to solve it in the Parallel Random Access Machine model; it may also be solved in linear time on a non-parallel computer using a stack-based algorithm. Later researchers have studied algorithms to solve it in other models of parallel computation.
A Fenwick tree or binary indexed tree(BIT) is a data structure that can efficiently update values and calculate prefix sums in an array of values.
In graph algorithms, the widest path problem is the problem of finding a path between two designated vertices in a weighted graph, maximizing the weight of the minimum-weight edge in the path. The widest path problem is also known as the maximum capacity path problem. It is possible to adapt most shortest path algorithms to compute widest paths, by modifying them to use the bottleneck distance instead of path length. However, in many cases even faster algorithms are possible.
In computer science, the range query problem consists of efficiently answering several queries regarding a given interval of elements within an array. For example, a common task, known as range minimum query, is finding the smallest value inside a given range within a list of numbers.
In graph theory and theoretical computer science, the level ancestor problem is the problem of preprocessing a given rooted tree T into a data structure that can determine the ancestor of a given node at a given distance from the root of the tree.
In computer science, the longest common prefix array is an auxiliary data structure to the suffix array. It stores the lengths of the longest common prefixes (LCPs) between all pairs of consecutive suffixes in a sorted suffix array.
In data structures, the range mode query problem asks to build a data structure on some input data to efficiently answer queries asking for the mode of any consecutive subset of the input.
In computer science, a Range Query Tree, or RQT, is a term for referring to a data structure that is used for performing range queries and updates on an underlying array, which is treated as the leaves of the tree. RQTs are, in principle, complete binary trees with a static structure, where each node stores the result of applying a fixed binary operation to a range of the tree's leaves.
In computer science, a generalized suffix array (GSA) is a suffix array containing all suffixes for a set of strings. Given the set of strings of total length , it is a lexicographically sorted array of all suffixes of each string in . It is primarily used in bioinformatics and string processing.