
In economics, the Gini coefficient, also known as the Gini index or Gini ratio, is a measure of statistical dispersion intended to represent the income inequality, the wealth inequality, or the consumption inequality within a nation or a social group. It was developed by Italian statistician and sociologist Corrado Gini.

Theoretical ecology is the scientific discipline devoted to the study of ecological systems using theoretical methods such as simple conceptual models, mathematical models, computational simulations, and advanced data analysis. Effective models improve understanding of the natural world by revealing how the dynamics of species populations are often based on fundamental biological conditions and processes. Further, the field aims to unify a diverse range of empirical observations by assuming that common, mechanistic processes generate observable phenomena across species and ecological environments. Based on biologically realistic assumptions, theoretical ecologists are able to uncover novel, non-intuitive insights about natural processes. Theoretical results are often verified by empirical and observational studies, revealing the power of theoretical methods in both predicting and understanding the noisy, diverse biological world.

Cross-validation, sometimes called rotation estimation or out-of-sample testing, is any of various similar model validation techniques for assessing how the results of a statistical analysis will generalize to an independent data set. Cross-validation includes resampling and sample splitting methods that use different portions of the data to test and train a model on different iterations. It is often used in settings where the goal is prediction, and one wants to estimate how accurately a predictive model will perform in practice. It can also be used to assess the quality of a fitted model and the stability of its parameters.
Species diversity is the number of different species that are represented in a given community. The effective number of species refers to the number of equally abundant species needed to obtain the same mean proportional species abundance as that observed in the dataset of interest. Meanings of species diversity may include species richness, taxonomic or phylogenetic diversity, and/or species evenness. Species richness is a simple count of species. Taxonomic or phylogenetic diversity is the genetic relationship between different groups of species. Species evenness quantifies how equal the abundances of the species are.

The unified neutral theory of biodiversity and biogeography is a theory and the title of a monograph by ecologist Stephen P. Hubbell. It aims to explain the diversity and relative abundance of species in ecological communities. Like other neutral theories of ecology, Hubbell assumes that the differences between members of an ecological community of trophically similar species are "neutral", or irrelevant to their success. This implies that niche differences do not influence abundance and the abundance of each species follows a random walk. The theory has sparked controversy, and some authors consider it a more complex version of other null models that fit the data better.

In probability and statistics, the logarithmic distribution is a discrete probability distribution derived from the Maclaurin series expansion
Insular biogeography or island biogeography is a field within biogeography that examines the factors that affect the species richness and diversification of isolated natural communities. The theory was originally developed to explain the pattern of the species–area relationship occurring in oceanic islands. Under either name it is now used in reference to any ecosystem that is isolated due to being surrounded by unlike ecosystems, and has been extended to mountain peaks, seamounts, oases, fragmented forests, and even natural habitats isolated by human land development. The field was started in the 1960s by the ecologists Robert H. MacArthur and E. O. Wilson, who coined the term island biogeography in their inaugural contribution to Princeton's Monograph in Population Biology series, which attempted to predict the number of species that would exist on a newly created island.
Random forests or random decision forests is an ensemble learning method for classification, regression and other tasks that operates by constructing a multitude of decision trees at training time. For classification tasks, the output of the random forest is the class selected by most trees. For regression tasks, the mean or average prediction of the individual trees is returned. Random decision forests correct for decision trees' habit of overfitting to their training set.

Species richness is the number of different species represented in an ecological community, landscape or region. Species richness is simply a count of species, and it does not take into account the abundances of the species or their relative abundance distributions. Species richness is sometimes considered synonymous with species diversity, but the formal metric species diversity takes into account both species richness and species evenness.
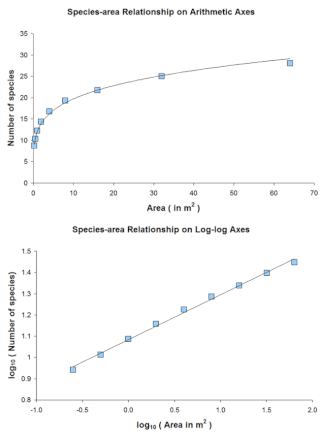
The species–area relationship or species–area curve describes the relationship between the area of a habitat, or of part of a habitat, and the number of species found within that area. Larger areas tend to contain larger numbers of species, and empirically, the relative numbers seem to follow systematic mathematical relationships. The species–area relationship is usually constructed for a single type of organism, such as all vascular plants or all species of a specific trophic level within a particular site. It is rarely if ever, constructed for all types of organisms if simply because of the prodigious data requirements. It is related but not identical to the species discovery curve.
The Theil index is a statistic primarily used to measure economic inequality and other economic phenomena, though it has also been used to measure racial segregation.
A diversity index is a quantitative measure that reflects how many different types there are in a dataset. More sophisticated indices accounting for the phylogenetic relatedness among the types. Diversity indices are statistical representations of different aspects of biodiversity, that are useful simplifications to compare different communities or sites.
In ecology, alpha diversity (α-diversity) is the mean species diversity in a site at a local scale. The term was introduced by R. H. Whittaker together with the terms beta diversity (β-diversity) and gamma diversity (γ-diversity). Whittaker's idea was that the total species diversity in a landscape is determined by two different things, the mean species diversity in sites at a more local scale and the differentiation among those sites.

Species richness, or biodiversity, increases from the poles to the tropics for a wide variety of terrestrial and marine organisms, often referred to as the latitudinal diversity gradient. The latitudinal diversity gradient is one of the most widely recognized patterns in ecology. It has been observed to varying degrees in Earth's past. A parallel trend has been found with elevation, though this is less well-studied.
In ecology, gamma diversity (γ-diversity) is the total species diversity in a landscape. The term was introduced by R. H. Whittaker together with the terms alpha diversity (α-diversity) and beta diversity (β-diversity). Whittaker's idea was that the total species diversity in a landscape (γ) is determined by two different things, the mean species diversity in sites at a more local scale (α) and the differentiation among those sites (β). According to this reasoning, alpha diversity and beta diversity constitute independent components of gamma diversity:

In statistics, the jackknife is a cross-validation technique and, therefore, a form of resampling. It is especially useful for bias and variance estimation. The jackknife pre-dates other common resampling methods such as the bootstrap. Given a sample of size , a jackknife estimator can be built by aggregating the parameter estimates from each subsample of size obtained by omitting one observation.
An index of qualitative variation (IQV) is a measure of statistical dispersion in nominal distributions. There are a variety of these, but they have been relatively little-studied in the statistics literature. The simplest is the variation ratio, while more complex indices include the information entropy.
Relative species abundance is a component of biodiversity and is a measure of how common or rare a species is relative to other species in a defined location or community. Relative abundance is the percent composition of an organism of a particular kind relative to the total number of organisms in the area. Relative species abundances tend to conform to specific patterns that are among the best-known and most-studied patterns in macroecology. Different populations in a community exist in relative proportions; this idea is known as relative abundance.

This is a list of topics in biodiversity.
The unseen species problem is commonly referred to in ecology and deals with the estimation of the number of species represented in an ecosystem that were not observed by samples. It more specifically relates to how many new species would be discovered if more samples were taken in an ecosystem. The study of the unseen species problem was started in the early 1940s by Alexander Steven Corbet. He spent 2 years in British Malaya trapping butterflies and was curious how many new species he would discover if he spent another 2 years trapping. Many different estimation methods have been developed to determine how many new species would be discovered given more samples. The unseen species problem also applies more broadly, as the estimators can be used to estimate any new elements of a set not previously found in samples. An example of this is determining how many words William Shakespeare knew based on all of his written works.


















