
In astronomy, Kepler's laws of planetary motion, published by Johannes Kepler between 1609 and 1619, describe the orbits of planets around the Sun. The laws modified the heliocentric theory of Nicolaus Copernicus, replacing its circular orbits and epicycles with elliptical trajectories, and explaining how planetary velocities vary. The three laws state that:
- The orbit of a planet is an ellipse with the Sun at one of the two foci.
- A line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time.
- The square of a planet's orbital period is proportional to the cube of the length of the semi-major axis of its orbit.

In mechanics and physics, simple harmonic motion is a special type of periodic motion an object experiences by means of a restoring force whose magnitude is directly proportional to the distance of the object from an equilibrium position and acts towards the equilibrium position. It results in an oscillation that is described by a sinusoid which continues indefinitely.

In celestial mechanics, escape velocity or escape speed is the minimum speed needed for an object to escape from contact with or orbit of a primary body, assuming:
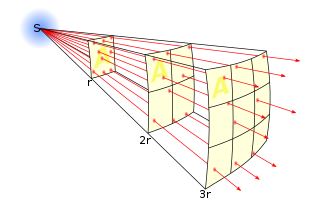
In science, an inverse-square law is any scientific law stating that the observed "intensity" of a specified physical quantity is inversely proportional to the square of the distance from the source of that physical quantity. The fundamental cause for this can be understood as geometric dilution corresponding to point-source radiation into three-dimensional space.
In classical mechanics, free fall is any motion of a body where gravity is the only force acting upon it. In the context of general relativity, where gravitation is reduced to a space-time curvature, a body in free fall has no force acting on it.

Orbital mechanics or astrodynamics is the application of ballistics and celestial mechanics to the practical problems concerning the motion of rockets, satellites, and other spacecraft. The motion of these objects is usually calculated from Newton's laws of motion and the law of universal gravitation. Orbital mechanics is a core discipline within space-mission design and control.
In continuum mechanics, the Froude number is a dimensionless number defined as the ratio of the flow inertia to the external force field. The Froude number is based on the speed–length ratio which he defined as: where u is the local flow velocity, g is the local gravity field, and L is a characteristic length.
In classical mechanics, the gravitational potential is a scalar field associating with each point in space the work per unit mass that would be needed to move an object to that point from a fixed reference point. It is analogous to the electric potential with mass playing the role of charge. The reference point, where the potential is zero, is by convention infinitely far away from any mass, resulting in a negative potential at any finite distance.
A sphere of influence (SOI) in astrodynamics and astronomy is the oblate-spheroid-shaped region where a particular celestial body exerts the main gravitational influence on an orbiting object. This is usually used to describe the areas in the Solar System where planets dominate the orbits of surrounding objects such as moons, despite the presence of the much more massive but distant Sun.
The Shapiro time delay effect, or gravitational time delay effect, is one of the four classic Solar System tests of general relativity. Radar signals passing near a massive object take slightly longer to travel to a target and longer to return than they would if the mass of the object were not present. The time delay is caused by time dilation, which increases the time it takes light to travel a given distance from the perspective of an outside observer. In a 1964 article entitled Fourth Test of General Relativity, Irwin Shapiro wrote:
Because, according to the general theory, the speed of a light wave depends on the strength of the gravitational potential along its path, these time delays should thereby be increased by almost 2×10−4 sec when the radar pulses pass near the sun. Such a change, equivalent to 60 km in distance, could now be measured over the required path length to within about 5 to 10% with presently obtainable equipment.
A classical field theory is a physical theory that predicts how one or more fields in physics interact with matter through field equations, without considering effects of quantization; theories that incorporate quantum mechanics are called quantum field theories. In most contexts, 'classical field theory' is specifically intended to describe electromagnetism and gravitation, two of the fundamental forces of nature.
The surface gravity, g, of an astronomical object is the gravitational acceleration experienced at its surface at the equator, including the effects of rotation. The surface gravity may be thought of as the acceleration due to gravity experienced by a hypothetical test particle which is very close to the object's surface and which, in order not to disturb the system, has negligible mass. For objects where the surface is deep in the atmosphere and the radius not known, the surface gravity is given at the 1 bar pressure level in the atmosphere.
In classical mechanics, the shell theorem gives gravitational simplifications that can be applied to objects inside or outside a spherically symmetrical body. This theorem has particular application to astronomy.

A gravity train is a theoretical means of transportation for purposes of commuting between two points on the surface of a sphere, by following a straight tunnel connecting the two points through the interior of the sphere.
Tensor–vector–scalar gravity (TeVeS), developed by Jacob Bekenstein in 2004, is a relativistic generalization of Mordehai Milgrom's Modified Newtonian dynamics (MOND) paradigm.
Scalar–tensor–vector gravity (STVG) is a modified theory of gravity developed by John Moffat, a researcher at the Perimeter Institute for Theoretical Physics in Waterloo, Ontario. The theory is also often referred to by the acronym MOG.

The gravity of Earth, denoted by g, is the net acceleration that is imparted to objects due to the combined effect of gravitation and the centrifugal force . It is a vector quantity, whose direction coincides with a plumb bob and strength or magnitude is given by the norm .
The gravity model of migration is a model in urban geography derived from Newton's law of gravity, and used to predict the degree of migration interaction between two places. Newton's law states that: "Any two bodies attract one another with a force that is proportional to the product of their masses and inversely proportional to the square of the distance between them."
The two-body problem in general relativity is the determination of the motion and gravitational field of two bodies as described by the field equations of general relativity. Solving the Kepler problem is essential to calculate the bending of light by gravity and the motion of a planet orbiting its sun. Solutions are also used to describe the motion of binary stars around each other, and estimate their gradual loss of energy through gravitational radiation.
Demographic gravitation is a concept of "social physics", introduced by Princeton University astrophysicist John Quincy Stewart in 1947. It is an attempt to use equations and notions of classical physics, such as gravity, to seek simplified insights and even laws of demographic behaviour for large numbers of human beings. A basic conception within it is that large numbers of people, in a city for example, actually behave as an attractive force for other people to migrate there. It has been related to W. J. Reilly's law of retail gravitation, George Kingsley Zipf's Demographic Energy, and to the theory of trip distribution through gravity models.











