A force is an influence that can cause an object to change its velocity unless counterbalanced by other forces. The concept of force makes the everyday notion of pushing or pulling mathematically precise. Because the magnitude and direction of a force are both important, force is a vector quantity. The SI unit of force is the newton (N), and force is often represented by the symbol F.

In physics, potential energy is the energy held by an object because of its position relative to other objects, stresses within itself, its electric charge, or other factors. The term potential energy was introduced by the 19th-century Scottish engineer and physicist William Rankine, although it has links to the ancient Greek philosopher Aristotle's concept of potentiality.
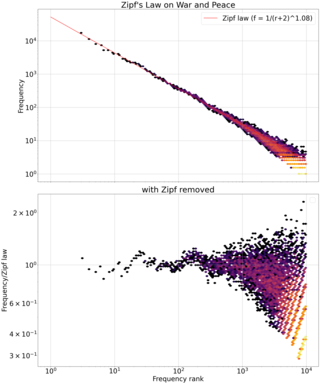
Zipf's law is an empirical law that often holds, approximately, when a list of measured values is sorted in decreasing order. It states that the value of the nth entry is inversely proportional to n.
In classical mechanics, free fall is any motion of a body where gravity is the only force acting upon it. In the context of general relativity, where gravitation is reduced to a space-time curvature, a body in free fall has no force acting on it.

The gravitational binding energy of a system is the minimum energy which must be added to it in order for the system to cease being in a gravitationally bound state. A gravitationally bound system has a lower gravitational potential energy than the sum of the energies of its parts when these are completely separated—this is what keeps the system aggregated in accordance with the minimum total potential energy principle.

In physics, a gravitational field or gravitational acceleration field is a vector field used to explain the influences that a body extends into the space around itself. A gravitational field is used to explain gravitational phenomena, such as the gravitational force field exerted on another massive body. It has dimension of acceleration (L/T2) and it is measured in units of newtons per kilogram (N/kg) or, equivalently, in meters per second squared (m/s2).

Poisson's equation is an elliptic partial differential equation of broad utility in theoretical physics. For example, the solution to Poisson's equation is the potential field caused by a given electric charge or mass density distribution; with the potential field known, one can then calculate the corresponding electrostatic or gravitational (force) field. It is a generalization of Laplace's equation, which is also frequently seen in physics. The equation is named after French mathematician and physicist Siméon Denis Poisson.
Newton's law of universal gravitation says that every particle attracts every other particle in the universe with a force that is proportional to the product of their masses and inversely proportional to the square of the distance between their centers. Separated objects attract and are attracted as if all their mass were concentrated at their centers. The publication of the law has become known as the "first great unification", as it marked the unification of the previously described phenomena of gravity on Earth with known astronomical behaviors.
In classical mechanics, the gravitational potential is a scalar field associating with each point in space the work per unit mass that would be needed to move an object to that point from a fixed reference point. It is analogous to the electric potential with mass playing the role of charge. The reference point, where the potential is zero, is by convention infinitely far away from any mass, resulting in a negative potential at any finite distance.

The equivalence principle is the hypothesis that the observed equivalence of gravitational and inertial mass is a consequence of nature. The weak form, known for centuries, relates to masses of any composition in free fall taking the same trajectories and landing at identical times. The extended form by Albert Einstein requires special relativity to also hold in free fall and requires the weak equivalence to be valid everywhere. This form was a critical input for the development of the theory of general relativity. The strong form requires Einstein's form to work for stellar objects. Highly precise experimental tests of the principle limit possible deviations from equivalence to be very small.

Trip distribution is the second component in the traditional four-step transportation forecasting model. This step matches tripmakers’ origins and destinations to develop a “trip table”, a matrix that displays the number of trips going from each origin to each destination. Historically, this component has been the least developed component of the transportation planning model.
A classical field theory is a physical theory that predicts how one or more fields in physics interact with matter through field equations, without considering effects of quantization; theories that incorporate quantum mechanics are called quantum field theories. In most contexts, 'classical field theory' is specifically intended to describe electromagnetism and gravitation, two of the fundamental forces of nature.

Hydraulic head or piezometric head is a specific measurement of liquid pressure above a vertical datum.
In economics, Reilly's law of retail gravitation is a heuristic developed by William J. Reilly in 1931. According to Reilly's "law," customers are willing to travel longer distances to larger retail centers given the higher attraction they present to customers. In Reilly's formulation, the attractiveness of the retail center becomes the analogy for size (mass) in the physical law of gravity.
In mathematical physics and differential geometry, a gravitational instanton is a four-dimensional complete Riemannian manifold satisfying the vacuum Einstein equations. They are so named because they are analogues in quantum theories of gravity of instantons in Yang–Mills theory. In accordance with this analogy with self-dual Yang–Mills instantons, gravitational instantons are usually assumed to look like four dimensional Euclidean space at large distances, and to have a self-dual Riemann tensor. Mathematically, this means that they are asymptotically locally Euclidean hyperkähler 4-manifolds, and in this sense, they are special examples of Einstein manifolds. From a physical point of view, a gravitational instanton is a non-singular solution of the vacuum Einstein equations with positive-definite, as opposed to Lorentzian, metric.
In theoretical physics, a scalar–tensor theory is a field theory that includes both a scalar field and a tensor field to represent a certain interaction. For example, the Brans–Dicke theory of gravitation uses both a scalar field and a tensor field to mediate the gravitational interaction.
Scalar–tensor–vector gravity (STVG) is a modified theory of gravity developed by John Moffat, a researcher at the Perimeter Institute for Theoretical Physics in Waterloo, Ontario. The theory is also often referred to by the acronym MOG.

Entropic gravity, also known as emergent gravity, is a theory in modern physics that describes gravity as an entropic force—a force with macro-scale homogeneity but which is subject to quantum-level disorder—and not a fundamental interaction. The theory, based on string theory, black hole physics, and quantum information theory, describes gravity as an emergent phenomenon that springs from the quantum entanglement of small bits of spacetime information. As such, entropic gravity is said to abide by the second law of thermodynamics under which the entropy of a physical system tends to increase over time.
In particle physics and physical cosmology, Planck units are a system of units of measurement defined exclusively in terms of four universal physical constants: c, G, ħ, and kB. Expressing one of these physical constants in terms of Planck units yields a numerical value of 1. They are a system of natural units, defined using fundamental properties of nature rather than properties of a chosen prototype object. Originally proposed in 1899 by German physicist Max Planck, they are relevant in research on unified theories such as quantum gravity.
Bimetric gravity or bigravity refers to two different classes of theories. The first class of theories relies on modified mathematical theories of gravity in which two metric tensors are used instead of one. The second metric may be introduced at high energies, with the implication that the speed of light could be energy-dependent, enabling models with a variable speed of light.
























