
In quantum mechanics, the particle in a box model describes the movement of a free particle in a small space surrounded by impenetrable barriers. The model is mainly used as a hypothetical example to illustrate the differences between classical and quantum systems. In classical systems, for example, a particle trapped inside a large box can move at any speed within the box and it is no more likely to be found at one position than another. However, when the well becomes very narrow, quantum effects become important. The particle may only occupy certain positive energy levels. Likewise, it can never have zero energy, meaning that the particle can never "sit still". Additionally, it is more likely to be found at certain positions than at others, depending on its energy level. The particle may never be detected at certain positions, known as spatial nodes.

The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary smooth potential can usually be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics. Furthermore, it is one of the few quantum-mechanical systems for which an exact, analytical solution is known.
The Schrödinger equation is a partial differential equation that governs the wave function of a non-relativistic quantum-mechanical system. Its discovery was a significant landmark in the development of quantum mechanics. It is named after Erwin Schrödinger, an Austrian physicist, who postulated the equation in 1925 and published it in 1926, forming the basis for the work that resulted in his Nobel Prize in Physics in 1933.

In physics, a wave packet is a short burst of localized wave action that travels as a unit, outlined by an envelope. A wave packet can be analyzed into, or can be synthesized from, a potentially-infinite set of component sinusoidal waves of different wavenumbers, with phases and amplitudes such that they interfere constructively only over a small region of space, and destructively elsewhere. Any signal of a limited width in time or space requires many frequency components around a center frequency within a bandwidth inversely proportional to that width; even a gaussian function is considered a wave packet because its Fourier transform is a "packet" of waves of frequencies clustered around a central frequency. Each component wave function, and hence the wave packet, are solutions of a wave equation. Depending on the wave equation, the wave packet's profile may remain constant or it may change while propagating.

In physics, the Rabi cycle is the cyclic behaviour of a two-level quantum system in the presence of an oscillatory driving field. A great variety of physical processes belonging to the areas of quantum computing, condensed matter, atomic and molecular physics, and nuclear and particle physics can be conveniently studied in terms of two-level quantum mechanical systems, and exhibit Rabi flopping when coupled to an optical driving field. The effect is important in quantum optics, magnetic resonance, and quantum computing, and is named after Isidor Isaac Rabi.
In physics, the S-matrix or scattering matrix is a matrix which relates the initial state and the final state of a physical system undergoing a scattering process. It is used in quantum mechanics, scattering theory and quantum field theory (QFT).
In physics, quantum tunnelling, barrier penetration, or simply tunnelling is a quantum mechanical phenomenon in which an object such as an electron or atom passes through a potential energy barrier that, according to classical mechanics, should not be passable due to the object not having sufficient energy to pass or surmount the barrier.
In mathematical physics, the WKB approximation or WKB method is a method for finding approximate solutions to linear differential equations with spatially varying coefficients. It is typically used for a semiclassical calculation in quantum mechanics in which the wavefunction is recast as an exponential function, semiclassically expanded, and then either the amplitude or the phase is taken to be changing slowly.

In theoretical physics, the pilot wave theory, also known as Bohmian mechanics, was the first known example of a hidden-variable theory, presented by Louis de Broglie in 1927. Its more modern version, the de Broglie–Bohm theory, interprets quantum mechanics as a deterministic theory, and avoids issues such as wave–particle duality, instantaneous wave function collapse, and the paradox of Schrödinger's cat by being inherently nonlocal.
In physics, a free particle is a particle that, in some sense, is not bound by an external force, or equivalently not in a region where its potential energy varies. In classical physics, this means the particle is present in a "field-free" space. In quantum mechanics, it means the particle is in a region of uniform potential, usually set to zero in the region of interest since the potential can be arbitrarily set to zero at any point in space.
The finite potential well is a concept from quantum mechanics. It is an extension of the infinite potential well, in which a particle is confined to a "box", but one which has finite potential "walls". Unlike the infinite potential well, there is a probability associated with the particle being found outside the box. The quantum mechanical interpretation is unlike the classical interpretation, where if the total energy of the particle is less than the potential energy barrier of the walls it cannot be found outside the box. In the quantum interpretation, there is a non-zero probability of the particle being outside the box even when the energy of the particle is less than the potential energy barrier of the walls.
In quantum mechanics, the probability current is a mathematical quantity describing the flow of probability. Specifically, if one thinks of probability as a heterogeneous fluid, then the probability current is the rate of flow of this fluid. It is a real vector that changes with space and time. Probability currents are analogous to mass currents in hydrodynamics and electric currents in electromagnetism. As in those fields, the probability current is related to the probability density function via a continuity equation. The probability current is invariant under gauge transformation.
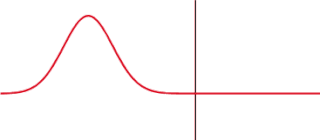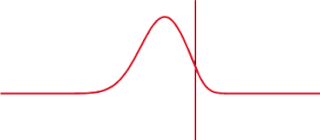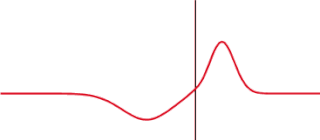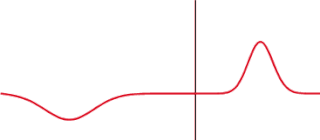
The transmission coefficient is used in physics and electrical engineering when wave propagation in a medium containing discontinuities is considered. A transmission coefficient describes the amplitude, intensity, or total power of a transmitted wave relative to an incident wave.
In quantum mechanics and scattering theory, the one-dimensional step potential is an idealized system used to model incident, reflected and transmitted matter waves. The problem consists of solving the time-independent Schrödinger equation for a particle with a step-like potential in one dimension. Typically, the potential is modeled as a Heaviside step function.

In quantum mechanics, the rectangularpotential barrier is a standard one-dimensional problem that demonstrates the phenomena of wave-mechanical tunneling and wave-mechanical reflection. The problem consists of solving the one-dimensional time-independent Schrödinger equation for a particle encountering a rectangular potential energy barrier. It is usually assumed, as here, that a free particle impinges on the barrier from the left.
In quantum mechanics the delta potential is a potential well mathematically described by the Dirac delta function - a generalized function. Qualitatively, it corresponds to a potential which is zero everywhere, except at a single point, where it takes an infinite value. This can be used to simulate situations where a particle is free to move in two regions of space with a barrier between the two regions. For example, an electron can move almost freely in a conducting material, but if two conducting surfaces are put close together, the interface between them acts as a barrier for the electron that can be approximated by a delta potential.
The Gross–Pitaevskii equation describes the ground state of a quantum system of identical bosons using the Hartree–Fock approximation and the pseudopotential interaction model.
In quantum mechanics and quantum field theory, a Schrödinger field, named after Erwin Schrödinger, is a quantum field which obeys the Schrödinger equation. While any situation described by a Schrödinger field can also be described by a many-body Schrödinger equation for identical particles, the field theory is more suitable for situations where the particle number changes.
The Gamow factor, Sommerfeld factor or Gamow–Sommerfeld factor, named after its discoverer George Gamow or after Arnold Sommerfeld, is a probability factor for two nuclear particles' chance of overcoming the Coulomb barrier in order to undergo nuclear reactions, for example in nuclear fusion. By classical physics, there is almost no possibility for protons to fuse by crossing each other's Coulomb barrier at temperatures commonly observed to cause fusion, such as those found in the Sun. When George Gamow instead applied quantum mechanics to the problem, he found that there was a significant chance for the fusion due to tunneling.
In pure and applied mathematics, quantum mechanics and computer graphics, a tensor operator generalizes the notion of operators which are scalars and vectors. A special class of these are spherical tensor operators which apply the notion of the spherical basis and spherical harmonics. The spherical basis closely relates to the description of angular momentum in quantum mechanics and spherical harmonic functions. The coordinate-free generalization of a tensor operator is known as a representation operator.













































