
In mathematics, a set B of vectors in a vector space V is called a basis if every element of V may be written in a unique way as a finite linear combination of elements of B. The coefficients of this linear combination are referred to as components or coordinates of the vector with respect to B. The elements of a basis are called basis vectors.
In mathematics, a coefficient is a multiplicative factor in some term of a polynomial, a series, or an expression; it is usually a number, but may be any expression. When the coefficients are themselves variables, they may also be called parameters.
In mathematics, the discriminant of a polynomial is a quantity that depends on the coefficients and allows deducing some properties of the roots without computing them. More precisely, it is a polynomial function of the coefficients of the original polynomial. The discriminant is widely used in polynomial factoring, number theory, and algebraic geometry.

In mathematics, orthogonality is the generalization of the notion of perpendicularity to the linear algebra of bilinear forms. Two elements u and v of a vector space with bilinear form B are orthogonal when B(u, v) = 0. Depending on the bilinear form, the vector space may contain nonzero self-orthogonal vectors. In the case of function spaces, families of orthogonal functions are used to form a basis.
Bézout's theorem is a statement in algebraic geometry concerning the number of common zeros of n polynomials in n indeterminates. In its original form the theorem states that in general the number of common zeros equals the product of the degrees of the polynomials. It is named after Étienne Bézout.
In commutative algebra and algebraic geometry, elimination theory is the classical name for algorithmic approaches to eliminating some variables between polynomials of several variables, in order to solve systems of polynomial equations.
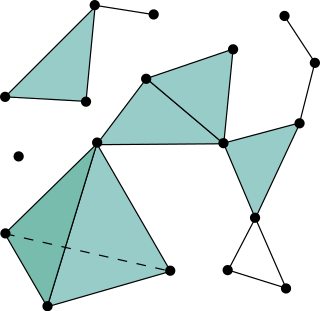
In mathematics, a simplicial complex is a set composed of points, line segments, triangles, and their n-dimensional counterparts. Simplicial complexes should not be confused with the more abstract notion of a simplicial set appearing in modern simplicial homotopy theory. The purely combinatorial counterpart to a simplicial complex is an abstract simplicial complex.

In mathematics, an affine space is a geometric structure that generalizes some of the properties of Euclidean spaces in such a way that these are independent of the concepts of distance and measure of angles, keeping only the properties related to parallelism and ratio of lengths for parallel line segments.
In mathematics, and more specifically in computer algebra, computational algebraic geometry, and computational commutative algebra, a Gröbner basis is a particular kind of generating set of an ideal in a polynomial ring K[x1, ..., xn] over a field K. A Gröbner basis allows many important properties of the ideal and the associated algebraic variety to be deduced easily, such as the dimension and the number of zeros when it is finite. Gröbner basis computation is one of the main practical tools for solving systems of polynomial equations and computing the images of algebraic varieties under projections or rational maps.
In mechanics, the net force is the vector sum of forces acting on a particle or object. The net force is a single force that replaces the effect of the original forces on the particle's motion. It gives the particle the same acceleration as all those actual forces together as described by Newton's second law of motion.
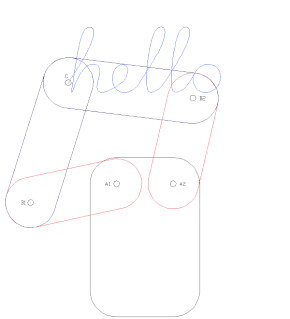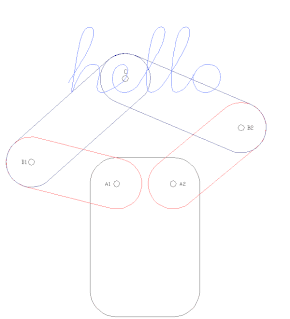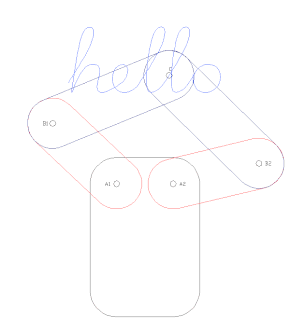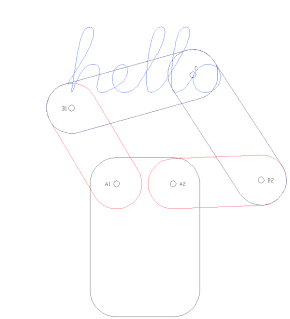
Robot kinematics applies geometry to the study of the movement of multi-degree of freedom kinematic chains that form the structure of robotic systems. The emphasis on geometry means that the links of the robot are modeled as rigid bodies and its joints are assumed to provide pure rotation or translation.
In mathematics, a homogeneous polynomial, sometimes called quantic in older texts, is a polynomial whose nonzero terms all have the same degree. For example, is a homogeneous polynomial of degree 5, in two variables; the sum of the exponents in each term is always 5. The polynomial is not homogeneous, because the sum of exponents does not match from term to term. The function defined by a homogeneous polynomial is always a homogeneous function.
In linear algebra, an eigenvector or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue, often denoted by , is the factor by which the eigenvector is scaled.
In mathematics, a Sylvester matrix is a matrix associated to two univariate polynomials with coefficients in a field or a commutative ring. The entries of the Sylvester matrix of two polynomials are coefficients of the polynomials. The determinant of the Sylvester matrix of two polynomials is their resultant, which is zero when the two polynomials have a common root or a non-constant common divisor.
Length in its basic meaning is the long dimension of an object.
In algebra, the greatest common divisor of two polynomials is a polynomial, of the highest possible degree, that is a factor of both the two original polynomials. This concept is analogous to the greatest common divisor of two integers.
In mathematics and physics, covariance is a measure of how much two variables change together, and may refer to:
A characteristic is a distinguishing feature of a person or thing. It may refer to:
This page is a glossary of terms in invariant theory. For descriptions of particular invariant rings, see invariants of a binary form, symmetric polynomials. For geometric terms used in invariant theory see the glossary of classical algebraic geometry. Definitions of many terms used in invariant theory can be found in, ,, ,, ,, , and the index to the fourth volume of Sylvester's collected works includes many of the terms invented by him.




