A force is an influence that can cause an object to change its velocity unless counterbalanced by other forces. The concept of force makes the everyday notion of pushing or pulling mathematically precise. Because the magnitude and direction of a force are both important, force is a vector quantity. The SI unit of force is the newton (N), and force is often represented by the symbol F.

In physics and mechanics, torque is the rotational analogue of linear force. It is also referred to as the moment of force. The symbol for torque is typically , the lowercase Greek letter tau. When being referred to as moment of force, it is commonly denoted by M. Just as a linear force is a push or a pull applied to a body, a torque can be thought of as a twist applied to an object with respect to a chosen point; for example, driving a screw uses torque, which is applied by the screwdriver rotating around its axis. A force of three newtons applied two metres from the fulcrum, for example, exerts the same torque as a force of one newton applied six metres from the fulcrum.

In science, work is the energy transferred to or from an object via the application of force along a displacement. In its simplest form, for a constant force aligned with the direction of motion, the work equals the product of the force strength and the distance traveled. A force is said to do positive work if it has a component in the direction of the displacement of the point of application. A force does negative work if it has a component opposite to the direction of the displacement at the point of application of the force.

The moment of inertia, otherwise known as the mass moment of inertia, angular/rotational mass, second moment of mass, or most accurately, rotational inertia, of a rigid body is a quantity that determines the torque needed for a desired angular acceleration about a rotational axis, akin to how mass determines the force needed for a desired acceleration. It depends on the body's mass distribution and the axis chosen, with larger moments requiring more torque to change the body's rate of rotation by a given amount.

In physics, the center of mass of a distribution of mass in space is the unique point at any given time where the weighted relative position of the distributed mass sums to zero. This is the point to which a force may be applied to cause a linear acceleration without an angular acceleration. Calculations in mechanics are often simplified when formulated with respect to the center of mass. It is a hypothetical point where the entire mass of an object may be assumed to be concentrated to visualise its motion. In other words, the center of mass is the particle equivalent of a given object for application of Newton's laws of motion.

In mechanics, the net force is the sum of all the forces acting on an object. For example, if two forces are acting upon an object in opposite directions, and one force is greater than the other, the forces can be replaced with a single force that is the difference of the greater and smaller force. That force is the net force.

In physics, a rigid body, also known as a rigid object, is a solid body in which deformation is zero or negligible. The distance between any two given points on a rigid body remains constant in time regardless of external forces or moments exerted on it. A rigid body is usually considered as a continuous distribution of mass.
In the physical science of dynamics, rigid-body dynamics studies the movement of systems of interconnected bodies under the action of external forces. The assumption that the bodies are rigid simplifies analysis, by reducing the parameters that describe the configuration of the system to the translation and rotation of reference frames attached to each body. This excludes bodies that display fluid, highly elastic, and plastic behavior.

D'Alembert's principle, also known as the Lagrange–d'Alembert principle, is a statement of the fundamental classical laws of motion. It is named after its discoverer, the French physicist and mathematician Jean le Rond d'Alembert, and Italian-French mathematician Joseph Louis Lagrange. D'Alembert's principle generalizes the principle of virtual work from static to dynamical systems by introducing forces of inertia which, when added to the applied forces in a system, result in dynamic equilibrium.
Dynamical simulation, in computational physics, is the simulation of systems of objects that are free to move, usually in three dimensions according to Newton's laws of dynamics, or approximations thereof. Dynamical simulation is used in computer animation to assist animators to produce realistic motion, in industrial design, and in video games. Body movement is calculated using time integration methods.
In classical mechanics, Euler's rotation equations are a vectorial quasilinear first-order ordinary differential equation describing the rotation of a rigid body, using a rotating reference frame with angular velocity ω whose axes are fixed to the body. Their general vector form is
In mechanics, virtual work arises in the application of the principle of least action to the study of forces and movement of a mechanical system. The work of a force acting on a particle as it moves along a displacement is different for different displacements. Among all the possible displacements that a particle may follow, called virtual displacements, one will minimize the action. This displacement is therefore the displacement followed by the particle according to the principle of least action.
The work of a force on a particle along a virtual displacement is known as the virtual work.
Screw theory is the algebraic calculation of pairs of vectors, such as angular and linear velocity, or forces and moments, that arise in the kinematics and dynamics of rigid bodies.

Rotation around a fixed axis or axial rotation is a special case of rotational motion around an axis of rotation fixed, stationary, or static in three-dimensional space. This type of motion excludes the possibility of the instantaneous axis of rotation changing its orientation and cannot describe such phenomena as wobbling or precession. According to Euler's rotation theorem, simultaneous rotation along a number of stationary axes at the same time is impossible; if two rotations are forced at the same time, a new axis of rotation will result.
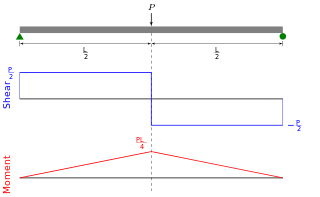
In solid mechanics, a bending moment is the reaction induced in a structural element when an external force or moment is applied to the element, causing the element to bend. The most common or simplest structural element subjected to bending moments is the beam. The diagram shows a beam which is simply supported at both ends; the ends can only react to the shear loads. Other beams can have both ends fixed ; therefore each end support has both bending moments and shear reaction loads. Beams can also have one end fixed and one end simply supported. The simplest type of beam is the cantilever, which is fixed at one end and is free at the other end. In reality, beam supports are usually neither absolutely fixed nor absolutely rotating freely.
In mechanics, a couple is a system of forces with a resultant moment of force but no resultant force.
In mechanics, a displacement field is the assignment of displacement vectors for all points in a region or body that are displaced from one state to another. A displacement vector specifies the position of a point or a particle in reference to an origin or to a previous position. For example, a displacement field may be used to describe the effects of deformation on a solid body.
In classical mechanics, Appell's equation of motion is an alternative general formulation of classical mechanics described by Josiah Willard Gibbs in 1879 and Paul Émile Appell in 1900.
In classical mechanics, Euler's laws of motion are equations of motion which extend Newton's laws of motion for point particle to rigid body motion. They were formulated by Leonhard Euler about 50 years after Isaac Newton formulated his laws.
Varignon's theorem is a theorem of French mathematician Pierre Varignon (1654–1722), published in 1687 in his book Projet d'une nouvelle mécanique. The theorem states that the torque of a resultant of two concurrent forces about any point is equal to the algebraic sum of the torques of its components about the same point. In other words, "If many concurrent forces are acting on a body, then the algebraic sum of torques of all the forces about a point in the plane of the forces is equal to the torque of their resultant about the same point."


























