Angular momentum is the rotational analog of linear momentum. It is an important physical quantity because it is a conserved quantity – the total angular momentum of a closed system remains constant. Angular momentum has both a direction and a magnitude, and both are conserved. Bicycles and motorcycles, flying discs, rifled bullets, and gyroscopes owe their useful properties to conservation of angular momentum. Conservation of angular momentum is also why hurricanes form spirals and neutron stars have high rotational rates. In general, conservation limits the possible motion of a system, but it does not uniquely determine it.
A force is an influence that can cause an object to change its velocity unless counterbalanced by other forces. The concept of force makes the everyday notion of pushing or pulling mathematically precise. Because the magnitude and direction of a force are both important, force is a vector quantity. The SI unit of force is the newton (N), and force is often represented by the symbol F.
Statics is the branch of classical mechanics that is concerned with the analysis of force and torque acting on a physical system that does not experience an acceleration, but rather is in equilibrium with its environment.

In physics and mechanics, torque is the rotational analogue of linear force. It is also referred to as the moment of force. The symbol for torque is typically , the lowercase Greek letter tau. When being referred to as moment of force, it is commonly denoted by M. Just as a linear force is a push or a pull applied to a body, a torque can be thought of as a twist applied to an object with respect to a chosen point; for example, driving a screw uses torque, which is applied by the screwdriver rotating around its axis. A force of three newtons applied two metres from the fulcrum, for example, exerts the same torque as a force of one newton applied six metres from the fulcrum.

In physics, equations of motion are equations that describe the behavior of a physical system in terms of its motion as a function of time. More specifically, the equations of motion describe the behavior of a physical system as a set of mathematical functions in terms of dynamic variables. These variables are usually spatial coordinates and time, but may include momentum components. The most general choice are generalized coordinates which can be any convenient variables characteristic of the physical system. The functions are defined in a Euclidean space in classical mechanics, but are replaced by curved spaces in relativity. If the dynamics of a system is known, the equations are the solutions for the differential equations describing the motion of the dynamics.
In physics, angular acceleration is the time rate of change of angular velocity. Following the two types of angular velocity, spin angular velocity and orbital angular velocity, the respective types of angular acceleration are: spin angular acceleration, involving a rigid body about an axis of rotation intersecting the body's centroid; and orbital angular acceleration, involving a point particle and an external axis.
In physics, a center of gravity of a material body is a point that may be used for a summary description of gravitational interactions. In a uniform gravitational field, the center of mass serves as the center of gravity. This is a very good approximation for smaller bodies near the surface of Earth, so there is no practical need to distinguish "center of gravity" from "center of mass" in most applications, such as engineering and medicine.

In science, work is the energy transferred to or from an object via the application of force along a displacement. In its simplest form, for a constant force aligned with the direction of motion, the work equals the product of the force strength and the distance traveled. A force is said to do positive work if it has a component in the direction of the displacement of the point of application. A force does negative work if it has a component opposite to the direction of the displacement at the point of application of the force.

The moment of inertia, otherwise known as the mass moment of inertia, angular/rotational mass, second moment of mass, or most accurately, rotational inertia, of a rigid body is defined relative to a rotational axis. It is the ratio between the torque applied and the resulting angular acceleration about that axis. It plays the same role in rotational motion as mass does in linear motion. A body's moment of inertia about a particular axis depends both on the mass and its distribution relative to the axis, increasing with mass & distance from the axis.

In physics, the center of mass of a distribution of mass in space is the unique point at any given time where the weighted relative position of the distributed mass sums to zero. For a rigid body containing its center of mass, this is the point to which a force may be applied to cause a linear acceleration without an angular acceleration. Calculations in mechanics are often simplified when formulated with respect to the center of mass. It is a hypothetical point where the entire mass of an object may be assumed to be concentrated to visualise its motion. In other words, the center of mass is the particle equivalent of a given object for application of Newton's laws of motion.

In physics, a rigid body, also known as a rigid object, is a solid body in which deformation is zero or negligible. The distance between any two given points on a rigid body remains constant in time regardless of external forces or moments exerted on it. A rigid body is usually considered as a continuous distribution of mass.
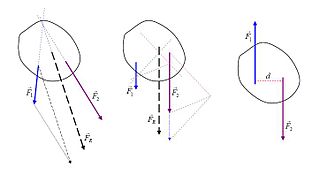
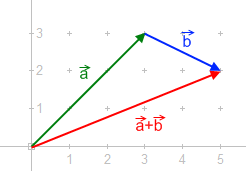
In physics and engineering, a resultant force is the single force and associated torque obtained by combining a system of forces and torques acting on a rigid body via vector addition. The defining feature of a resultant force, or resultant force-torque, is that it has the same effect on the rigid body as the original system of forces. Calculating and visualizing the resultant force on a body is done through computational analysis, or a free body diagram.
In the physical science of dynamics, rigid-body dynamics studies the movement of systems of interconnected bodies under the action of external forces. The assumption that the bodies are rigid simplifies analysis, by reducing the parameters that describe the configuration of the system to the translation and rotation of reference frames attached to each body. This excludes bodies that display fluid, highly elastic, and plastic behavior.
In physics, circular motion is a movement of an object along the circumference of a circle or rotation along a circular arc. It can be uniform, with a constant rate of rotation and constant tangential speed, or non-uniform with a changing rate of rotation. The rotation around a fixed axis of a three-dimensional body involves the circular motion of its parts. The equations of motion describe the movement of the center of mass of a body, which remains at a constant distance from the axis of rotation. In circular motion, the distance between the body and a fixed point on its surface remains the same, i.e., the body is assumed rigid.

Rolling is a type of motion that combines rotation and translation of that object with respect to a surface, such that, if ideal conditions exist, the two are in contact with each other without sliding.
In mechanics, virtual work arises in the application of the principle of least action to the study of forces and movement of a mechanical system. The work of a force acting on a particle as it moves along a displacement is different for different displacements. Among all the possible displacements that a particle may follow, called virtual displacements, one will minimize the action. This displacement is therefore the displacement followed by the particle according to the principle of least action.
The work of a force on a particle along a virtual displacement is known as the virtual work.
In classical mechanics, the Newton–Euler equations describe the combined translational and rotational dynamics of a rigid body.

Rotation around a fixed axis or axial rotation is a special case of rotational motion around an axis of rotation fixed, stationary, or static in three-dimensional space. This type of motion excludes the possibility of the instantaneous axis of rotation changing its orientation and cannot describe such phenomena as wobbling or precession. According to Euler's rotation theorem, simultaneous rotation along a number of stationary axes at the same time is impossible; if two rotations are forced at the same time, a new axis of rotation will result.
In physics, a couple is a system of forces with a resultant moment of force but no resultant force.
In classical mechanics, Euler's laws of motion are equations of motion which extend Newton's laws of motion for point particle to rigid body motion. They were formulated by Leonhard Euler about 50 years after Isaac Newton formulated his laws.