Related Research Articles
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Informally, the notion of a natural transformation states that a particular map between functors can be done consistently over an entire category.
In mathematics, specifically in homology theory and algebraic topology, cohomology is a general term for a sequence of abelian groups, usually one associated with a topological space, often defined from a cochain complex. Cohomology can be viewed as a method of assigning richer algebraic invariants to a space than homology. Some versions of cohomology arise by dualizing the construction of homology. In other words, cochains are functions on the group of chains in homology theory.
In category theory, a branch of mathematics, a monad is a monoid in the category of endofunctors of some fixed category. An endofunctor is a functor mapping a category to itself, and a monad is an endofunctor together with two natural transformations required to fulfill certain coherence conditions. Monads are used in the theory of pairs of adjoint functors, and they generalize closure operators on partially ordered sets to arbitrary categories. Monads are also useful in the theory of datatypes, the denotational semantics of imperative programming languages, and in functional programming languages, allowing languages without mutable state to do things such as simulate for-loops; see Monad.
In mathematics, an H-space is a homotopy-theoretic version of a generalization of the notion of topological group, in which the axioms on associativity and inverses are removed.
In mathematics, complex cobordism is a generalized cohomology theory related to cobordism of manifolds. Its spectrum is denoted by MU. It is an exceptionally powerful cohomology theory, but can be quite hard to compute, so often instead of using it directly one uses some slightly weaker theories derived from it, such as Brown–Peterson cohomology or Morava K-theory, that are easier to compute.
In algebraic topology, a branch of mathematics, a spectrum is an object representing a generalized cohomology theory. Every such cohomology theory is representable, as follows from Brown's representability theorem. This means that, given a cohomology theory
,

In the mathematical field of algebraic topology, the homotopy groups of spheres describe how spheres of various dimensions can wrap around each other. They are examples of topological invariants, which reflect, in algebraic terms, the structure of spheres viewed as topological spaces, forgetting about their precise geometry. Unlike homology groups, which are also topological invariants, the homotopy groups are surprisingly complex and difficult to compute.
In mathematics, especially in the fields of representation theory and module theory, a Frobenius algebra is a finite-dimensional unital associative algebra with a special kind of bilinear form which gives the algebras particularly nice duality theories. Frobenius algebras began to be studied in the 1930s by Richard Brauer and Cecil Nesbitt and were named after Georg Frobenius. Tadashi Nakayama discovered the beginnings of a rich duality theory, . Jean Dieudonné used this to characterize Frobenius algebras. Frobenius algebras were generalized to quasi-Frobenius rings, those Noetherian rings whose right regular representation is injective. In recent times, interest has been renewed in Frobenius algebras due to connections to topological quantum field theory.
In mathematics, stable homotopy theory is the part of homotopy theory concerned with all structure and phenomena that remain after sufficiently many applications of the suspension functor. A founding result was the Freudenthal suspension theorem, which states that given any pointed space , the homotopy groups stabilize for sufficiently large. In particular, the homotopy groups of spheres stabilize for . For example,
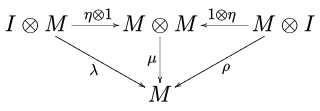
In category theory, a branch of mathematics, a monoid (or monoid object, or internal monoid, or algebra) (M, μ, η) in a monoidal category (C, ⊗, I) is an object M together with two morphisms
In mathematics, specifically algebraic topology, there is a distinguished class of spectra called Eilenberg–Maclane spectra for any Abelian group pg 134. Note, this construction can be generalized to commutative rings as well from its underlying Abelian group. These are an important class of spectra because they model ordinary integral cohomology and cohomology with coefficients in an abelian group. In addition, they are a lift of the homological structure in the derived category of abelian groups in the homotopy category of spectra. In addition, these spectra can be used to construct resolutions of spectra, called Adams resolutions, which are used in the construction of the Adams spectral sequence.
In stable homotopy theory, a branch of mathematics, the sphere spectrumS is the monoidal unit in the category of spectra. It is the suspension spectrum of S0, i.e., a set of two points. Explicitly, the nth space in the sphere spectrum is the n-dimensional sphere Sn, and the structure maps from the suspension of Sn to Sn+1 are the canonical homeomorphisms. The k-th homotopy group of a sphere spectrum is the k-th stable homotopy group of spheres.
In mathematics, a highly structured ring spectrum or -ring is an object in homotopy theory encoding a refinement of a multiplicative structure on a cohomology theory. A commutative version of an -ring is called an -ring. While originally motivated by questions of geometric topology and bundle theory, they are today most often used in stable homotopy theory.
In mathematics, in the theory of Hopf algebras, a Hopf algebroid is a generalisation of weak Hopf algebras, certain skew Hopf algebras and commutative Hopf k-algebroids. If k is a field, a commutative k-algebroid is a cogroupoid object in the category of k-algebras; the category of such is hence dual to the category of groupoid k-schemes. This commutative version has been used in 1970-s in algebraic geometry and stable homotopy theory. The generalization of Hopf algebroids and its main part of the structure, associative bialgebroids, to the noncommutative base algebra was introduced by J.-H. Lu in 1996 as a result on work on groupoids in Poisson geometry. They may be loosely thought of as Hopf algebras over a noncommutative base ring, where weak Hopf algebras become Hopf algebras over a separable algebra. It is a theorem that a Hopf algebroid satisfying a finite projectivity condition over a separable algebra is a weak Hopf algebra, and conversely a weak Hopf algebra H is a Hopf algebroid over its separable subalgebra HL. The antipode axioms have been changed by G. Böhm and K. Szlachányi in 2004 for tensor categorical reasons and to accommodate examples associated to depth two Frobenius algebra extensions.
In mathematics, weak bialgebras are a generalization of bialgebras that are both algebras and coalgebras but for which the compatibility conditions between the two structures have been "weakened". In the same spirit, weak Hopf algebras are weak bialgebras together with a linear map S satisfying specific conditions; they are generalizations of Hopf algebras.
In algebra, a simplicial commutative ring is a commutative monoid in the category of simplicial abelian groups, or, equivalently, a simplicial object in the category of commutative rings. If A is a simplicial commutative ring, then it can be shown that is a ring and are modules over that ring
This is a glossary of properties and concepts in algebraic topology in mathematics.
In mathematics, specifically algebraic topology, there is a resolution analogous to free resolutions of spectra yielding a tool for constructing the Adams spectral sequence. Essentially, the idea is to take a connective spectrum of finite type and iteratively resolve with other spectra that are in the homotopy kernel of a map resolving the cohomology classes in using Eilenberg–MacLane spectra.
In mathematics, specifically homotopical algebra, an H-object is a categorical generalization of an H-space, which can be defined in any category with a product and an initial object . These are useful constructions because they help export some of the ideas from algebraic topology and homotopy theory into other domains, such as in commutative algebra and algebraic geometry.
References
- Adams, J. Frank (1974), Stable homotopy and generalised homology, Chicago Lectures in Mathematics, University of Chicago Press, ISBN 0-226-00523-2, MR 0402720