Rosser's equation (physics)

Last updated December 18, 2019

In physics, Rosser's equation aids in understanding the role of displacement current in Maxwell's equations, given that there is no aether in empty space as initially assumed by Maxwell. Due originally to William G.V. Rosser,^[1] the equation was labeled by Selvan:^[2]

“

It can thus be seen that Rosser's Equation (19) in terms of transverse current density has actually hidden away the displacement current.

”

Equation

Rosser's Equation is given by the following:

$-\mu _{0}\mathbf {J} +\mu _{0}\varepsilon _{0}\nabla {\frac {\partial \phi }{\partial t}}=-\mu _{0}\left(\mathbf {J} -\varepsilon _{0}\nabla {\frac {\partial \phi }{\partial t}}\right)=-\mu _{0}\mathbf {J_{t}}$

where:

J\,

is the conduction-current density,

J_{t}\,

is the transverse current density,

t\,

is time, and

\phi \,

is the scalar potential.

To understand Selvan's quotation we need the following terms: $\rho$ is charge density, $\mathbf {A}$ is the magnetic vector potential, and $\mathbf {D}$ is the displacement field. Given these, the following standard Maxwell relations hold:

$\nabla \cdot \left(-\nabla \phi -{\frac {\partial \mathbf {A} }{\partial t}}\right)={\frac {\rho }{\varepsilon _{0}}}$

$\mu _{0}\left(\mathbf {J} +{\frac {\partial \mathbf {D} }{\partial t}}\right)=-\nabla ^{2}\mathbf {A}$

The term ${\frac {\partial \mathbf {D} }{\partial t}}$ is the displacement current that Selvan notes is "hidden away" in Rosser's Equation. Selvan (ibid.) quotes Rosser himself as follows:

“

A lot of confusion about the role of the displacement current in empty space might be avoided, if it were called something else that did not include the term current. If a name is needed, it could be called the Maxwell term in honour of the man who first introduced it.

”

Related Research Articles

Maxwell's equations are a set of coupled partial differential equations that, together with the Lorentz force law, form the foundation of classical electromagnetism, classical optics, and electric circuits. The equations provide a mathematical model for electric, optical, and radio technologies, such as power generation, electric motors, wireless communication, lenses, radar etc. Maxwell's equations describe how electric and magnetic fields are generated by charges, currents, and changes of the fields. An important consequence of the equations is that they demonstrate how fluctuating electric and magnetic fields propagate at a constant speed (c) in a vacuum. Known as electromagnetic radiation, these waves may occur at various wavelengths to produce a spectrum of light from radio waves to γ-rays. The equations are named after the physicist and mathematician James Clerk Maxwell, who published an early form of the equations that included the Lorentz force law between 1861 and 1862. Maxwell first used the equations to propose that light is an electromagnetic phenomenon.

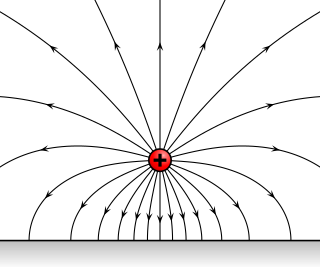
An electric field surrounds an electric charge, and exerts force on other charges in the field, attracting or repelling them. Electric field is sometimes abbreviated as E-field. The electric field is defined mathematically as a vector field that associates to each point in space the force per unit of charge exerted on an infinitesimal positive test charge at rest at that point. The SI unit for electric field strength is volt per meter (V/m). Newtons per coulomb (N/C) is also used as a unit of electric field strength. Electric fields are created by electric charges, or by time-varying magnetic fields. Electric fields are important in many areas of physics, and are exploited practically in electrical technology. On an atomic scale, the electric field is responsible for the attractive force between the atomic nucleus and electrons that holds atoms together, and the forces between atoms that cause chemical bonding. Electric fields and magnetic fields are both manifestations of the electromagnetic force, one of the four fundamental forces of nature.

In mathematics, Poisson's equation is a partial differential equation of elliptic type with broad utility in mechanical engineering and theoretical physics. It arises, for instance, to describe the potential field caused by a given charge or mass density distribution; with the potential field known, one can then calculate gravitational or electrostatic field. It is a generalization of Laplace's equation, which is also frequently seen in physics. The equation is named after the French mathematician, geometer, and physicist Siméon Denis Poisson.

In classical electromagnetism, Ampère's circuital law relates the integrated magnetic field around a closed loop to the electric current passing through the loop. James Clerk Maxwell derived it using hydrodynamics in his 1861 paper "On Physical Lines of Force" and it is now one of the Maxwell equations, which form the basis of classical electromagnetism.

Linear elasticity is a mathematical model of how solid objects deform and become internally stressed due to prescribed loading conditions. It is a simplification of the more general nonlinear theory of elasticity and a branch of continuum mechanics.

In the calculus of variations, a field of mathematical analysis, the functional derivative relates a change in a functional to a change in a function on which the functional depends.

In electromagnetism, displacement current density is the quantity $\partial D /\partial t$ appearing in Maxwell's equations that is defined in terms of the rate of change of $D$ , the electric displacement field. Displacement current density has the same units as electric current density, and it is a source of the magnetic field just as actual current is. However it is not an electric current of moving charges, but a time-varying electric field. In physical materials, there is also a contribution from the slight motion of charges bound in atoms, called dielectric polarization.

"A Dynamical Theory of the Electromagnetic Field" is a paper by James Clerk Maxwell on electromagnetism, published in 1865. In the paper, Maxwell derives an electromagnetic wave equation with a velocity for light in close agreement with measurements made by experiment, and deduces that light is an electromagnetic wave.

The term magnetic potential can be used for either of two quantities in classical electromagnetism: the magnetic vector potential, or simply vector potential, A; and the magnetic scalar potentialψ. Both quantities can be used in certain circumstances to calculate the magnetic field B.

In electromagnetism, the Lorenz gauge condition or Lorenz gauge is a partial gauge fixing of the electromagnetic vector potential. The condition is that $This does not completely determine the gauge: one can still make a gauge transformation where is a harmonic scalar function.$

The electromagnetic wave equation is a second-order partial differential equation that describes the propagation of electromagnetic waves through a medium or in a vacuum. It is a three-dimensional form of the wave equation. The homogeneous form of the equation, written in terms of either the electric field $E$ or the magnetic field $B$ , takes the form:

In electromagnetism, Jefimenko's equations give the electric field and magnetic field due to a distribution of electric charges and electric current in space, that takes into account the propagation delay of the fields due to the finite speed of light and relativistic effects. Therefore they can be used for moving charges and currents. They are the general solutions to Maxwell's equations for any arbitrary distribution of charges and currents.

Lorentz–Heaviside units constitute a system of units within CGS, named from Hendrik Antoon Lorentz and Oliver Heaviside. They share with CGS-Gaussian units the property that the electric constant $ε 0$ and magnetic constant $µ 0$ do not appear, having been incorporated implicitly into the unit system and electromagnetic equations. Lorentz–Heaviside units may be regarded as normalizing $ε 0 = 1$ and $µ 0 = 1$ , while at the same time revising Maxwell's equations to use the speed of light $c$ instead.

The magnetic tension force is a restoring force that acts to straighten bent magnetic field lines. It equals:

In electromagnetism and applications, an inhomogeneous electromagnetic wave equation, or nonhomogeneous electromagnetic wave equation, is one of a set of wave equations describing the propagation of electromagnetic waves generated by nonzero source charges and currents. The source terms in the wave equations make the partial differential equations inhomogeneous, if the source terms are zero the equations reduce to the homogeneous electromagnetic wave equations. The equations follow from Maxwell's equations.

The Newman–Penrose (NP) formalism is a set of notation developed by Ezra T. Newman and Roger Penrose for general relativity (GR). Their notation is an effort to treat general relativity in terms of spinor notation, which introduces complex forms of the usual variables used in GR. The NP formalism is itself a special case of the tetrad formalism, where the tensors of the theory are projected onto a complete vector basis at each point in spacetime. Usually this vector basis is chosen to reflect some symmetry of the spacetime, leading to simplified expressions for physical observables. In the case of the NP formalism, the vector basis chosen is a null tetrad: a set of four null vectors—two real, and a complex-conjugate pair. The two real members asymptotically point radially inward and radially outward, and the formalism is well adapted to treatment of the propagation of radiation in curved spacetime. The Weyl scalars, derived from the Weyl tensor, are often used. In particular, it can be shown that one of these scalars— $in the appropriate frame—encodes the outgoing gravitational radiation of an asymptotically flat system.$

There are various mathematical descriptions of the electromagnetic field that are used in the study of electromagnetism, one of the four fundamental interactions of nature. In this article, several approaches are discussed, although the equations are in terms of electric and magnetic fields, potentials, and charges with currents, generally speaking.

In electrodynamics, the retarded potentials are the electromagnetic potentials for the electromagnetic field generated by time-varying electric current or charge distributions in the past. The fields propagate at the speed of light c, so the delay of the fields connecting cause and effect at earlier and later times is an important factor: the signal takes a finite time to propagate from a point in the charge or current distribution to another point in space, see figure below.

In continuum mechanics, a compatible deformation tensor field in a body is that unique tensor field that is obtained when the body is subjected to a continuous, single-valued, displacement field. Compatibility is the study of the conditions under which such a displacement field can be guaranteed. Compatibility conditions are particular cases of integrability conditions and were first derived for linear elasticity by Barré de Saint-Venant in 1864 and proved rigorously by Beltrami in 1886.

Lagrangian field theory is a formalism in classical field theory. It is the field-theoretic analogue of Lagrangian mechanics. Lagrangian mechanics is used for discrete particles each with a finite number of degrees of freedom. Lagrangian field theory applies to continua and fields, which have an infinite number of degrees of freedom.

References

↑ Rosser, W.G.V., 1976, December. "Does the Displacement Current in Empty Space Produce a Magnetic Field?" American Journal of Physics, vol. 44, no. 12, pp. 1221-1223.
↑ Selvan, T. Krishnasamy, 2009, June. "A Revisiting of Scientific and Philosophical Perspectives on Maxwell's Displacement Current," IEEE Antennas and Propagation Magazine, vol. 51, no. 3, pp. 36-46.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Rosser, W.G.V., 1976, December. "Does the Displacement Current in Empty Space Produce a Magnetic Field?" American Journal of Physics, vol. 44, no. 12, pp. 1221-1223.

[2] Selvan, T. Krishnasamy, 2009, June. "A Revisiting of Scientific and Philosophical Perspectives on Maxwell's Displacement Current," IEEE Antennas and Propagation Magazine, vol. 51, no. 3, pp. 36-46.