Rotating unbalance is the uneven distribution of mass around an axis of rotation. A rotating mass, or rotor, is said to be out of balance when its center of mass (inertia axis) is out of alignment with the center of rotation (geometric axis). Unbalance causes a moment which gives the rotor a wobbling movement characteristic of vibration of rotating structures.
A static balance (sometimes called a force balance [2] [3] ) occurs when the inertial axis of a rotating mass is displaced from and parallel to the axis of rotation. Static unbalances can occur more frequently in disk-shaped rotors because the thin geometric profile of the disk allows for an uneven distribution of mass with an inertial axis that is nearly parallel to the axis of rotation. Only one plane receives balance correction. [4]
where U = balance, m = mass, r = distance between unbalance and the centre of the object
A couple balance occurs when a rotating mass has two equal unbalance forces that are situated 180° opposite each other. A system that is statically balanced may still have a couple unbalance. Couple unbalance occurs frequently in elongated cylindrical rotors.
where d = distance between the two unbalance forces along the rotation axis.
In rotation an unbalance when the mass/inertia axis does not intersect with shaft axis then it is called dynamic balance. Combination of static and couple balance is dynamic unbalance. It occurs in virtually all rotors and is the most common kind of unbalance. It can be fixed by correcting the weight on at least two planes. [5]
The measurement of existing vibration and calculation of the change of mass required is typically carried out using some form of balancing machine.
ISO 21940 [6] classifies vibration in terms of G codes. Unfortunately, it is the theoretical value assuming the rotor was spinning in free space so it does not relate to actual operating conditions. Rotors of the same type having permissible residual specific unbalance value eper, varies inversely with the speed of the rotor.
where ω = angular velocity (radians per second) eper = permissible residual specific unbalance
This constant is quality grade G. Balance Grades are used to specify the allowable residual imbalance for rotating machinery. The ISO 1940 standard defines balance grades for different classes of machinery. A rotor balanced to G2.5 will vibrate at 2.5 mm/s at operating speed if rotating in a suspended state with no external influences.
Where Uper = balance tolerance (or) residual imbalance
Where F = force due to unbalance, U = unbalance. ω = angular frequency. e = specific unbalance. m = mass. r = distance between unbalance and the axis of rotation of the object.
Isaac Newton's rotating bucket argument was designed to demonstrate that true rotational motion cannot be defined as the relative rotation of the body with respect to the immediately surrounding bodies. It is one of five arguments from the "properties, causes, and effects" of "true motion and rest" that support his contention that, in general, true motion and rest cannot be defined as special instances of motion or rest relative to other bodies, but instead can be defined only by reference to absolute space. Alternatively, these experiments provide an operational definition of what is meant by "absolute rotation", and do not pretend to address the question of "rotation relative to what?" General relativity dispenses with absolute space and with physics whose cause is external to the system, with the concept of geodesics of spacetime.
In physics, the Coriolis force is an inertial or fictitious force that acts on objects in motion within a frame of reference that rotates with respect to an inertial frame. In a reference frame with clockwise rotation, the force acts to the left of the motion of the object. In one with anticlockwise rotation, the force acts to the right. Deflection of an object due to the Coriolis force is called the Coriolis effect. Though recognized previously by others, the mathematical expression for the Coriolis force appeared in an 1835 paper by French scientist Gaspard-Gustave de Coriolis, in connection with the theory of water wheels. Early in the 20th century, the term Coriolis force began to be used in connection with meteorology.
In physics, jerk or jolt is the rate at which an object's acceleration changes with respect to time. It is a vector quantity. Jerk is most commonly denoted by the symbol j and expressed in m/s3 or standard gravities per second (g0/s).
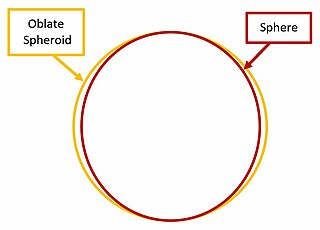
An equatorial bulge is a difference between the equatorial and polar diameters of a planet, due to the centrifugal force exerted by the rotation about the body's axis. A rotating body tends to form an oblate spheroid rather than a sphere.
In fluid dynamics, a vortex is a region in a fluid in which the flow revolves around an axis line, which may be straight or curved. Vortices form in stirred fluids, and may be observed in smoke rings, whirlpools in the wake of a boat, and the winds surrounding a tropical cyclone, tornado or dust devil.
Rotational–vibrational spectroscopy is a branch of molecular spectroscopy concerned with infrared and Raman spectra of molecules in the gas phase. Transitions involving changes in both vibrational and rotational states can be abbreviated as rovibrational transitions. When such transitions emit or absorb photons, the frequency is proportional to the difference in energy levels and can be detected by certain kinds of spectroscopy. Since changes in rotational energy levels are typically much smaller than changes in vibrational energy levels, changes in rotational state are said to give fine structure to the vibrational spectrum. For a given vibrational transition, the same theoretical treatment as for pure rotational spectroscopy gives the rotational quantum numbers, energy levels, and selection rules. In linear and spherical top molecules, rotational lines are found as simple progressions at both higher and lower frequencies relative to the pure vibration frequency. In symmetric top molecules the transitions are classified as parallel when the dipole moment change is parallel to the principal axis of rotation, and perpendicular when the change is perpendicular to that axis. The ro-vibrational spectrum of the asymmetric rotor water is important because of the presence of water vapor in the atmosphere.
Rotational spectroscopy is concerned with the measurement of the energies of transitions between quantized rotational states of molecules in the gas phase. The spectra of polar molecules can be measured in absorption or emission by microwave spectroscopy or by far infrared spectroscopy. The rotational spectra of non-polar molecules cannot be observed by those methods, but can be observed and measured by Raman spectroscopy. Rotational spectroscopy is sometimes referred to as pure rotational spectroscopy to distinguish it from rotational-vibrational spectroscopy where changes in rotational energy occur together with changes in vibrational energy, and also from ro-vibronic spectroscopy where rotational, vibrational and electronic energy changes occur simultaneously.
Rolling is a type of motion that combines rotation and translation of that object with respect to a surface, such that, if ideal conditions exist, the two are in contact with each other without sliding.
The rigid rotor is a mechanical model of rotating systems. An arbitrary rigid rotor is a 3-dimensional rigid object, such as a top. To orient such an object in space requires three angles, known as Euler angles. A special rigid rotor is the linear rotor requiring only two angles to describe, for example of a diatomic molecule. More general molecules are 3-dimensional, such as water, ammonia, or methane.
Engine balance refers to how the forces are balanced within an internal combustion engine or steam engine. The most commonly used terms are primary balance and secondary balance. First-order balance and second-order balance are also used. Unbalanced forces within the engine can lead to vibrations.
Rotation around a fixed axis is a special case of rotational motion. The fixed-axis hypothesis excludes the possibility of an axis changing its orientation and cannot describe such phenomena as wobbling or precession. According to Euler's rotation theorem, simultaneous rotation along a number of stationary axes at the same time is impossible; if two rotations are forced at the same time, a new axis of rotation will appear.
In physics, rotational–vibrational coupling occurs when the rotation frequency of a system is close to or identical to a natural internal vibration frequency. The animation on the right shows ideal motion, with the force exerted by the spring and the distance from the center of rotation increasing together linearly with no friction.
A balancing machine is a measuring tool used for balancing rotating machine parts such as rotors for electric motors, fans, turbines, disc brakes, disc drives, propellers and pumps. The machine usually consists of two rigid pedestals, with suspension and bearings on top supporting a mounting platform. The unit under test is bolted to the platform and is rotated either with a belt-, air-, or end-drive. As the part is rotated, the vibration in the suspension is detected with sensors and that information is used to determine the amount of unbalance in the part. Along with phase information, the machine can determine how much and where to add or remove weights to balance the part.
In solid mechanics, in the field of rotordynamics, the critical speed is the theoretical angular velocity that excites the natural frequency of a rotating object, such as a shaft, propeller, leadscrew, or gear. As the speed of rotation approaches the object's natural frequency, the object begins to resonate, which dramatically increases system vibration. The resulting resonance occurs regardless of orientation. When the rotational speed is equal to the numerical value of the natural vibration, then that speed is referred to as critical speed.
Rotordynamics, also known as rotor dynamics, is a specialized branch of applied mechanics concerned with the behavior and diagnosis of rotating structures. It is commonly used to analyze the behavior of structures ranging from jet engines and steam turbines to auto engines and computer disk storage. At its most basic level, rotor dynamics is concerned with one or more mechanical structures (rotors) supported by bearings and influenced by internal phenomena that rotate around a single axis. The supporting structure is called a stator. As the speed of rotation increases the amplitude of vibration often passes through a maximum that is called a critical speed. This amplitude is commonly excited by imbalance of the rotating structure; everyday examples include engine balance and tire balance. If the amplitude of vibration at these critical speeds is excessive, then catastrophic failure occurs. In addition to this, turbomachinery often develop instabilities which are related to the internal makeup of turbomachinery, and which must be corrected. This is the chief concern of engineers who design large rotors.
Tire balance, also called tire unbalance or tire imbalance, describes the distribution of mass within an automobile tire or the entire wheel on which it is mounted.
In Newtonian mechanics, the centrifugal force is an inertial force that appears to act on all objects when viewed in a rotating frame of reference. It is directed away from an axis which is parallel to the axis of rotation and passing through the coordinate system's origin. If the axis of rotation passes through the coordinate system's origin, the centrifugal force is directed radially outwards from that axis. The magnitude of centrifugal force F on an object of mass m at the distance r from the origin of a frame of reference rotating with angular velocity ω is:
Isaac Newton's rotating spheres argument attempts to demonstrate that true rotational motion can be defined by observing the tension in the string joining two identical spheres. The basis of the argument is that all observers make two observations: the tension in the string joining the bodies and the rate of rotation of the spheres. Only for the truly non-rotating observer will the tension in the string be explained using only the observed rate of rotation. For all other observers a "correction" is required that accounts for the tension calculated being different from the one expected using the observed rate of rotation. It is one of five arguments from the "properties, causes, and effects" of true motion and rest that support his contention that, in general, true motion and rest cannot be defined as special instances of motion or rest relative to other bodies, but instead can be defined only by reference to absolute space. Alternatively, these experiments provide an operational definition of what is meant by "absolute rotation", and do not pretend to address the question of "rotation relative to what?" General relativity dispenses with absolute space and with physics whose cause is external to the system, with the concept of geodesics of spacetime.
Vibration is a mechanical phenomenon whereby oscillations occur about an equilibrium point. The word comes from Latin vibrationem. The oscillations may be periodic, such as the motion of a pendulum—or random, such as the movement of a tire on a gravel road.
The balancing of rotating bodies is important to avoid vibration. In heavy industrial machines such as gas turbines and electric generators, vibration can cause catastrophic failure, as well as noise and discomfort. In the case of a narrow wheel, balancing simply involves moving the center of gravity to the centre of rotation. For a system to be in complete balance both force and couple polygons should be close in order to prevent the effect of centrifugal force. It is important to design the machine parts wisely so that the unbalance is reduced up to the minimum possible level or eliminated completely.
