 | This article needs additional citations for verification .(June 2020) (Learn how and when to remove this template message) |
In combinatorics, the rule of division is a counting principle. It states that there are n/d ways to do a task if it can be done using a procedure that can be carried out in n ways, and for each way w, exactly d of the n ways correspond to the way w. In a nutshell, the division rule is a common way to ignore "unimportant" differences when counting things. [1]
In the terms of a set: "If the finite set A is the union of n pairwise disjoint subsets each with d elements, then n = |A|/d." [1]
The rule of division formulated in terms of functions: "If f is a function from A to B where A and B are finite sets, and that for every value y ∈ B there are exactly d values x ∈ A such that f (x) = y (in which case, we say that f is d-to-one), then |B| = |A|/d." [1]
Example 1
- How many different ways are there to seat four people around a circular table, where two seatings are considered the same when each person has the same left neighbor and the same right neighbor?
Example 2
- We have 6 coloured bricks in total, 4 of them are red and 2 are white, in how many ways can we arrange them?
In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A countable set is either a finite set or a countably infinite set. Whether finite or infinite, the elements of a countable set can always be counted one at a time and—although the counting may never finish—every element of the set is associated with a unique natural number.
In mathematics, the four color theorem, or the four color map theorem, states that, given any separation of a plane into contiguous regions, producing a figure called a map, no more than four colors are required to color the regions of the map so that no two adjacent regions have the same color. Adjacent means that two regions share a common boundary curve segment, not merely a corner where three or more regions meet. It was the first major theorem to be proved using a computer. Initially, this proof was not accepted by all mathematicians because the computer-assisted proof was infeasible for a human to check by hand. Since then the proof has gained wide acceptance, although some doubters remain.
In mathematics, a finite field or Galois field is a field that contains a finite number of elements. As with any field, a finite field is a set on which the operations of multiplication, addition, subtraction and division are defined and satisfy certain basic rules. The most common examples of finite fields are given by the integers mod p when p is a prime number.
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints. In other words, it can be drawn in such a way that no edges cross each other. Such a drawing is called a plane graph or planar embedding of the graph. A plane graph can be defined as a planar graph with a mapping from every node to a point on a plane, and from every edge to a plane curve on that plane, such that the extreme points of each curve are the points mapped from its end nodes, and all curves are disjoint except on their extreme points.
In mathematics, especially in abstract algebra, a quasigroup is an algebraic structure resembling a group in the sense that "division" is always possible. Quasigroups differ from groups mainly in that they are not necessarily associative.
Sprouts is a paper-and-pencil game that can be enjoyed simply by both adults and children. Yet it also can be analyzed for its significant mathematical properties. It was invented by mathematicians John Horton Conway and Michael S. Paterson at Cambridge University in the early 1960s. Setup is even simpler than the popular Dots and Boxes game, but game-play develops much more artistically and organically.
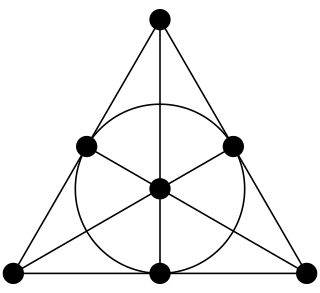
In combinatorial mathematics, a Steiner system is a type of block design, specifically a t-design with λ = 1 and t ≥ 2.
In computer science, a universal Turing machine (UTM) is a Turing machine that simulates an arbitrary Turing machine on arbitrary input. The universal machine essentially achieves this by reading both the description of the machine to be simulated as well as the input to that machine from its own tape. Alan Turing introduced the idea of such a machine in 1936–1937. This principle is considered to be the origin of the idea of a stored-program computer used by John von Neumann in 1946 for the "Electronic Computing Instrument" that now bears von Neumann's name: the von Neumann architecture.
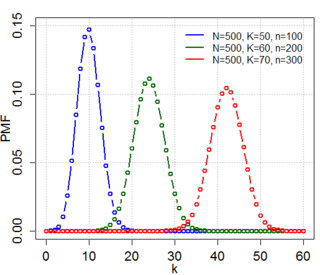
In probability theory and statistics, the hypergeometric distribution is a discrete probability distribution that describes the probability of successes in draws, without replacement, from a finite population of size that contains exactly objects with that feature, wherein each draw is either a success or a failure. In contrast, the binomial distribution describes the probability of successes in draws with replacement.
In combinatorial mathematics, Ramsey's theorem, in one of its graph-theoretic forms, states that one will find monochromatic cliques in any edge labelling of a sufficiently large complete graph. To demonstrate the theorem for two colours, let r and s be any two positive integers. Ramsey's theorem states that there exists a least positive integer R(r, s) for which every blue-red edge colouring of the complete graph on R(r, s) vertices contains a blue clique on r vertices or a red clique on s vertices.
In combinatorics, the rule of product or multiplication principle is a basic counting principle. Stated simply, it is the idea that if there are a ways of doing something and b ways of doing another thing, then there are a · b ways of performing both actions.
Named after the 19th century British mathematician Arthur Cayley, a Cayley table describes the structure of a finite group by arranging all the possible products of all the group's elements in a square table reminiscent of an addition or multiplication table. Many properties of a group – such as whether or not it is abelian, which elements are inverses of which elements, and the size and contents of the group's center – can be discovered from its Cayley table.
Induction puzzles are logic puzzles, which are examples of multi-agent reasoning, where the solution evolves along with the principle of induction.
Combinatorial design theory is the part of combinatorial mathematics that deals with the existence, construction and properties of systems of finite sets whose arrangements satisfy generalized concepts of balance and/or symmetry. These concepts are not made precise so that a wide range of objects can be thought of as being under the same umbrella. At times this might involve the numerical sizes of set intersections as in block designs, while at other times it could involve the spatial arrangement of entries in an array as in sudoku grids.
In combinatorics, the twelvefold way is a systematic classification of 12 related enumerative problems concerning two finite sets, which include the classical problems of counting permutations, combinations, multisets, and partitions either of a set or of a number. The idea of the classification is credited to Gian-Carlo Rota, and the name was suggested by Joel Spencer.
Pattern theory, formulated by Ulf Grenander, is a mathematical formalism to describe knowledge of the world as patterns. It differs from other approaches to artificial intelligence in that it does not begin by prescribing algorithms and machinery to recognize and classify patterns; rather, it prescribes a vocabulary to articulate and recast the pattern concepts in precise language. Broad in its mathematical coverage, Pattern Theory spans algebra and statistics, as well as local topological and global entropic properties.
In mathematics, more specifically field theory, the degree of a field extension is a rough measure of the "size" of the field extension. The concept plays an important role in many parts of mathematics, including algebra and number theory — indeed in any area where fields appear prominently.
Boolean algebra is a mathematically rich branch of abstract algebra. Just as group theory deals with groups, and linear algebra with vector spaces, Boolean algebras are models of the equational theory of the two values 0 and 1. Common to Boolean algebras, groups, and vector spaces is the notion of an algebraic structure, a set closed under zero or more operations satisfying certain equations.
In combinatorial mathematics, the ménage problem or problème des ménages asks for the number of different ways in which it is possible to seat a set of male-female couples at a round dining table so that men and women alternate and nobody sits next to his or her partner. This problem was formulated in 1891 by Édouard Lucas and independently, a few years earlier, by Peter Guthrie Tait in connection with knot theory. For a number of couples equal to 3, 4, 5, ... the number of seating arrangements is
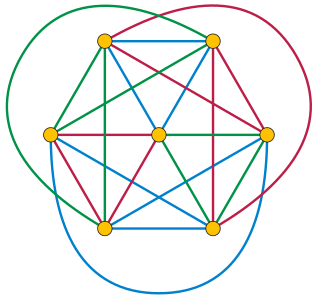
The Oberwolfach problem is an unsolved problem in mathematics that may be formulated either as a problem of scheduling seating assignments for diners, or more abstractly as a problem in graph theory, on the edge cycle covers of complete graphs. It is named after the Mathematical Research Institute of Oberwolfach, where the problem was posed in 1967 by Gerhard Ringel.