In algebraic topology, an -object (also called a symmetric sequence) is a sequence of objects such that each comes with an action [note 1] of the symmetric group .
The category of combinatorial species is equivalent to the category of finite -sets (roughly because the permutation category is equivalent to the category of finite sets and bijections.) [1]
By -module, we mean an -object in the category of finite-dimensional vector spaces over a field k of characteristic zero (the symmetric groups act from the right by convention). Then each -module determines a Schur functor on .
This definition of -module shares its name with the considerably better-known model for highly structured ring spectra due to Elmendorf, Kriz, Mandell and May.[ clarification needed ]
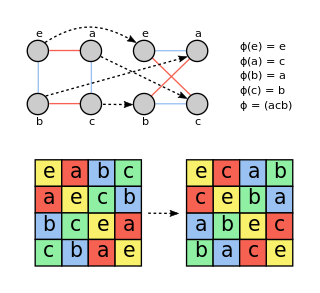
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism group. It is, loosely speaking, the symmetry group of the object.
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties.
In mathematics, a direct limit is a way to construct a object from many objects that are put together in a specific way. These objects may be groups, rings, vector spaces or in general objects from any category. The way they are put together is specified by a system of homomorphisms between those smaller objects. The direct limit of the objects , where ranges over some directed set , is denoted by . This notation suppresses the system of homomorphisms; however, the limit depends on the system of homomorphisms.
In mathematics, K-theory is, roughly speaking, the study of a ring generated by vector bundles over a topological space or scheme. In algebraic topology, it is a cohomology theory known as topological K-theory. In algebra and algebraic geometry, it is referred to as algebraic K-theory. It is also a fundamental tool in the field of operator algebras. It can be seen as the study of certain kinds of invariants of large matrices.
In mathematics, a monoidal category is a category equipped with a bifunctor
In category theory, a branch of mathematics, a monad is a triple consisting of a functor T from a category to itself and two natural transformations that satisfy the conditions like associativity. For example, if are functors adjoint to each other, then together with determined by the adjoint relation is a monad.
In mathematics, especially in the area of abstract algebra known as module theory, an injective module is a module Q that shares certain desirable properties with the Z-module Q of all rational numbers. Specifically, if Q is a submodule of some other module, then it is already a direct summand of that module; also, given a submodule of a module Y, any module homomorphism from this submodule to Q can be extended to a homomorphism from all of Y to Q. This concept is dual to that of projective modules. Injective modules were introduced in and are discussed in some detail in the textbook.
In mathematics, the Ext functors are the derived functors of the Hom functor. Along with the Tor functor, Ext is one of the core concepts of homological algebra, in which ideas from algebraic topology are used to define invariants of algebraic structures. The cohomology of groups, Lie algebras, and associative algebras can all be defined in terms of Ext. The name comes from the fact that the first Ext group Ext1 classifies extensions of one module by another.
In mathematics, especially in category theory, a closed monoidal category is a category that is both a monoidal category and a closed category in such a way that the structures are compatible.
In mathematics, the Grothendieck group, or group of differences, of a commutative monoid M is a certain abelian group. This abelian group is constructed from M in the most universal way, in the sense that any abelian group containing a homomorphic image of M will also contain a homomorphic image of the Grothendieck group of M. The Grothendieck group construction takes its name from a specific case in category theory, introduced by Alexander Grothendieck in his proof of the Grothendieck–Riemann–Roch theorem, which resulted in the development of K-theory. This specific case is the monoid of isomorphism classes of objects of an abelian category, with the direct sum as its operation.
In mathematics, especially in the fields of representation theory and module theory, a Frobenius algebra is a finite-dimensional unital associative algebra with a special kind of bilinear form which gives the algebras particularly nice duality theories. Frobenius algebras began to be studied in the 1930s by Richard Brauer and Cecil Nesbitt and were named after Georg Frobenius. Tadashi Nakayama discovered the beginnings of a rich duality theory, . Jean Dieudonné used this to characterize Frobenius algebras. Frobenius algebras were generalized to quasi-Frobenius rings, those Noetherian rings whose right regular representation is injective. In recent times, interest has been renewed in Frobenius algebras due to connections to topological quantum field theory.
In mathematics, an operad is a structure that consists of abstract operations, each one having a fixed finite number of inputs (arguments) and one output, as well as a specification of how to compose these operations. Given an operad , one defines an algebra over to be a set together with concrete operations on this set which behave just like the abstract operations of . For instance, there is a Lie operad such that the algebras over are precisely the Lie algebras; in a sense abstractly encodes the operations that are common to all Lie algebras. An operad is to its algebras as a group is to its group representations.
In abstract algebra, Morita equivalence is a relationship defined between rings that preserves many ring-theoretic properties. More precisely two rings like R, S are Morita equivalent if their categories of modules are additively equivalent. It is named after Japanese mathematician Kiiti Morita who defined equivalence and a similar notion of duality in 1958.
In category theory, a branch of mathematics, a dual object is an analogue of a dual vector space from linear algebra for objects in arbitrary monoidal categories. It is only a partial generalization, based upon the categorical properties of duality for finite-dimensional vector spaces. An object admitting a dual is called a dualizable object. In this formalism, infinite-dimensional vector spaces are not dualizable, since the dual vector space V∗ doesn't satisfy the axioms. Often, an object is dualizable only when it satisfies some finiteness or compactness property.
In mathematics a stack or 2-sheaf is, roughly speaking, a sheaf that takes values in categories rather than sets. Stacks are used to formalise some of the main constructions of descent theory, and to construct fine moduli stacks when fine moduli spaces do not exist.
In mathematics, a Grothendieck category is a certain kind of abelian category, introduced in Alexander Grothendieck's Tôhoku paper of 1957 in order to develop the machinery of homological algebra for modules and for sheaves in a unified manner. The theory of these categories was further developed in Pierre Gabriel's seminal thesis in 1962.
In algebra, Quillen's Q-construction associates to an exact category an algebraic K-theory. More precisely, given an exact category C, the construction creates a topological space so that is the Grothendieck group of C and, when C is the category of finitely generated projective modules over a ring R, for , is the i-th K-group of R in the classical sense. One puts
This is a glossary of properties and concepts in algebraic topology in mathematics.
In representation theory, the category of representations of some algebraic structure A has the representations of A as objects and equivariant maps as morphisms between them. One of the basic thrusts of representation theory is to understand the conditions under which this category is semisimple; i.e., whether an object decomposes into simple objects.
In mathematics, the automorphism group of an object X is the group consisting of automorphisms of X under composition of morphisms. For example, if X is a finite-dimensional vector space, then the automorphism group of X is the group of invertible linear transformations from X to itself. If instead X is a group, then its automorphism group is the group consisting of all group automorphisms of X.
 | This topology-related article is a stub. You can help Wikipedia by expanding it. |
