Related Research Articles

In mathematics and computational geometry, a Delaunay triangulation for a given set P of discrete points in a plane is a triangulation DT(P) such that no point in P is inside the circumcircle of any triangle in DT(P). Delaunay triangulations maximize the minimum angle of all the angles of the triangles in the triangulation; they tend to avoid sliver triangles. The triangulation is named after Boris Delaunay for his work on this topic from 1934.
In computer science, a priority queue is an abstract data type similar to a regular queue or stack data structure in which each element additionally has a "priority" associated with it. In a priority queue, an element with high priority is served before an element with low priority. In some implementations, if two elements have the same priority, they are served according to the order in which they were enqueued, while in other implementations, ordering of elements with the same priority is undefined.

Dijkstra's algorithm is an algorithm for finding the shortest paths between nodes in a graph, which may represent, for example, road networks. It was conceived by computer scientist Edsger W. Dijkstra in 1956 and published three years later.

In computer science, Prim'salgorithm is a greedy algorithm that finds a minimum spanning tree for a weighted undirected graph. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized. The algorithm operates by building this tree one vertex at a time, from an arbitrary starting vertex, at each step adding the cheapest possible connection from the tree to another vertex.
Collision detection is the computational problem of detecting the intersection of two or more objects. Collision detection is a classic issue of computational geometry and has applications in various computing fields, primarily in computer graphics, computer games, computer simulations, robotics and computational physics. Collision detection algorithms can be divided into operating on 2D and 3D objects.
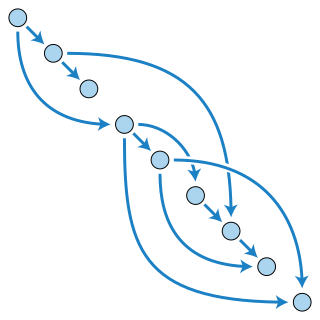
In mathematics, particularly graph theory, and computer science, a directed acyclic graph is a directed graph with no directed cycles. That is, it consists of vertices and edges, with each edge directed from one vertex to another, such that there is no way to start at any vertex v and follow a consistently-directed sequence of edges that eventually loops back to v again. Equivalently, a DAG is a directed graph that has a topological ordering, a sequence of the vertices such that every edge is directed from earlier to later in the sequence.

In computer science, the clique problem is the computational problem of finding cliques in a graph. It has several different formulations depending on which cliques, and what information about the cliques, should be found. Common formulations of the clique problem include finding a maximum clique, finding a maximum weight clique in a weighted graph, listing all maximal cliques, and solving the decision problem of testing whether a graph contains a clique larger than a given size.

A dragon curve is any member of a family of self-similar fractal curves, which can be approximated by recursive methods such as Lindenmayer systems. The dragon curve is probably most commonly thought of as the shape that is generated from repeatedly folding a strip of paper in half, although there are other curves that are called dragon curves that are generated differently.
In mathematics, Sperner's lemma is a combinatorial analog of the Brouwer fixed point theorem, which is equivalent to it.

In computational geometry, polygon triangulation is the decomposition of a polygonal area P into a set of triangles, i.e., finding a set of triangles with pairwise non-intersecting interiors whose union is P.

In graph theory, a maximal independent set (MIS) or maximal stable set is an independent set that is not a subset of any other independent set. In other words, there is no vertex outside the independent set that may join it because it is maximal with respect to the independent set property.

In computer science and electrical engineering, Lloyd's algorithm, also known as Voronoi iteration or relaxation, is an algorithm named after Stuart P. Lloyd for finding evenly spaced sets of points in subsets of Euclidean spaces and partitions of these subsets into well-shaped and uniformly sized convex cells. Like the closely related k-means clustering algorithm, it repeatedly finds the centroid of each set in the partition and then re-partitions the input according to which of these centroids is closest. In this setting, the mean operation is an integral over a region of space, and the nearest centroid operation results in Voronoi diagrams.
The Christofides algorithm or Christofides–Serdyukov algorithm is an algorithm for finding approximate solutions to the travelling salesman problem, on instances where the distances form a metric space . It is an approximation algorithm that guarantees that its solutions will be within a factor of 3/2 of the optimal solution length, and is named after Nicos Christofides and Anatoliy I. Serdyukov, who discovered it independently in 1976.
A triangle strip is a series of connected triangles from the triangle mesh, sharing vertices, allowing for more efficient memory usage for computer graphics. They are more efficient than triangle lists without indexing, but usually equally fast or slower than indexed triangle lists. The primary reason to use triangle strips is to reduce the amount of data needed to create a series of triangles. The number of vertices stored in memory is reduced from 3N to N+2, where N is the number of triangles to be drawn. This allows for less use of disk space, as well as making them faster to load into RAM.

In the mathematical area of graph theory, a triangle-free graph is an undirected graph in which no three vertices form a triangle of edges. Triangle-free graphs may be equivalently defined as graphs with clique number ≤ 2, graphs with girth ≥ 4, graphs with no induced 3-cycle, or locally independent graphs.
In computational geometry, the Bowyer–Watson algorithm is a method for computing the Delaunay triangulation of a finite set of points in any number of dimensions. The algorithm can be also used to obtain a Voronoi diagram of the points, which is the dual graph of the Delaunay triangulation.

In mesh generation, Ruppert's algorithm, also known as Delaunay refinement, is an algorithm for creating quality Delaunay triangulations. The algorithm takes a planar straight-line graph and returns a conforming Delaunay triangulation of only quality triangles. A triangle is considered poor-quality if it has a circumradius to shortest edge ratio larger than some prescribed threshold. Discovered by Jim Ruppert in the early 1990s, "Ruppert's algorithm for two-dimensional quality mesh generation is perhaps the first theoretically guaranteed meshing algorithm to be truly satisfactory in practice."
In linguistic morphology and information retrieval, stemming is the process of reducing inflected words to their word stem, base or root form—generally a written word form. The stem need not be identical to the morphological root of the word; it is usually sufficient that related words map to the same stem, even if this stem is not in itself a valid root. Algorithms for stemming have been studied in computer science since the 1960s. Many search engines treat words with the same stem as synonyms as a kind of query expansion, a process called conflation.

Quickhull is a method of computing the convex hull of a finite set of points in n-dimensional space. It uses a divide and conquer approach similar to that of quicksort, from which its name derives. Its worst case complexity for 2-dimensional and 3-dimensional space is considered to be , where is the number of input points and is the number of processed points. However, unlike quicksort, there is no obvious way to convert quickhull into a randomized algorithm. Thus, its average time complexity cannot be easily calculated.
The Möller–Trumbore ray-triangle intersection algorithm, named after its inventors Tomas Möller and Ben Trumbore, is a fast method for calculating the intersection of a ray and a triangle in three dimensions without needing precomputation of the plane equation of the plane containing the triangle. Among other uses, it can be used in computer graphics to implement ray tracing computations involving triangle meshes.
References
- 1 2 Francine Evans; Steven Skiena & Amitabh Varshney (1996). Optimizing triangle strips for fast rendering (PDF). Visualization 1996. IEEE. pp. 319–326. Retrieved 2012-08-31.