Scale co-occurrence matrix

Last updated August 20, 2024

Scale co-occurrence matrix (SCM) is a method for image feature extraction within scale space after wavelet transformation, proposed by Wu Jun and Zhao Zhongming (Institute of Remote Sensing Application, China). In practice, we first do discrete wavelet transformation for one gray image and get sub images with different scales. Then we construct a series of scale based concurrent matrices, every matrix describing the gray level variation between two adjacent scales. Last we use selected functions (such as Harris statistical approach) to calculate measurements with SCM and do feature extraction and classification. One basis of the method is the fact: way texture information changes from one scale to another can represent that texture in some extent thus it can be used as a criterion for feature extraction. The matrix captures the relation of features between different scales rather than the features within a single scale space, which can represent the scale property of texture better. Also, there are several experiments showing that it can get more accurate results for texture classification than the traditional texture classification.^[1]

Background

Texture can be regarded as a similarity grouping in an image. Traditional texture analysis can be divided into four major issues: feature extraction, texture discrimination, texture classification and shape from texture(to reconstruct 3D surface geometry from texture information). For tradition feature extraction, approaches are usually categorized into structural, statistical, model based and transform.^[2] Wavelet transformation is a popular method in numerical analysis and functional analysis, which captures both frequency and location information. Gray level co-occurrence matrix provides an important basis for SCM construction. SCM based on discrete wavelet frame transformation make use of both correlations and feature information so that it combines structural and statistical benefits.

Discrete wavelet frame (DWF)

In order to do SCM we have to use discrete wavelet frame (DWF) transformation first to get a series of sub images. The discrete wavelet frames is nearly identical to the standard wavelet transform,^[3] except that one upsamples the filters, rather than downsamples the image. Given an image, the DWF decomposes its channel using the same method as the wavelet transform, but without the subsampling process. This results in four filtered images with the same size as the input image. The decomposition is then continued in the LL channels only as in the wavelet transform, but since the image is not subsampled, the filter has to be upsampled by inserting zeros in between its coefficients. The number of channels, hence the number of features for DWF is given by 3 × l − 1.^[4] One dimension discrete wavelet frame decompose the image in this way:

d_{i}(k)=[[g_{i}]^{T}x],\quad (i=1,\ldots ,N)

Example

If there are two sub images X₁ and X₀ from the parent image X (in practice X = X₀), X₁ = [1 1;1 2], X₂ = [1 1;1 4],the grayscale is 4 so that we can get k = 1, G = 4. X₁(1,1), (1,2) and (2,1) are 1, while X₀(1,1), (1,2) and (2,1) are 1, thus Φ₁(1,1) = 3; Similarly, Φ₁(2,4) = 1. The SCM is as following:

G=4	Gray level 0	Gray level 2
Gray level 0	0	0
Gray level 1	3	0
Gray level 2	0	0
Gray level 3	0	0
Gray level 4	0	1

External links

Tao Chen; Kai-Kuang Ma; Li-Hui Chen (1998). "Discrete wavelet frame representations of color texture features for image query". 1998 IEEE Second Workshop on Multimedia Signal Processing (Cat. No.98EX175). IEEE. pp. 45–50. doi:10.1109/MMSP.1998.738911. ISBN 0-7803-4919-9. S2CID 1833240.
co-occurrence-matrix MATLAB tutorial
Co-occurrence Matrix

Related Research Articles

Digital signal processing (DSP) is the use of digital processing, such as by computers or more specialized digital signal processors, to perform a wide variety of signal processing operations. The digital signals processed in this manner are a sequence of numbers that represent samples of a continuous variable in a domain such as time, space, or frequency. In digital electronics, a digital signal is represented as a pulse train, which is typically generated by the switching of a transistor.

Image compression is a type of data compression applied to digital images, to reduce their cost for storage or transmission. Algorithms may take advantage of visual perception and the statistical properties of image data to provide superior results compared with generic data compression methods which are used for other digital data.

A wavelet is a wave-like oscillation with an amplitude that begins at zero, increases or decreases, and then returns to zero one or more times. Wavelets are termed a "brief oscillation". A taxonomy of wavelets has been established, based on the number and direction of its pulses. Wavelets are imbued with specific properties that make them useful for signal processing.

Digital image processing is the use of a digital computer to process digital images through an algorithm. As a subcategory or field of digital signal processing, digital image processing has many advantages over analog image processing. It allows a much wider range of algorithms to be applied to the input data and can avoid problems such as the build-up of noise and distortion during processing. Since images are defined over two dimensions digital image processing may be modeled in the form of multidimensional systems. The generation and development of digital image processing are mainly affected by three factors: first, the development of computers; second, the development of mathematics ; third, the demand for a wide range of applications in environment, agriculture, military, industry and medical science has increased.

<span class="mw-page-title-main">Daubechies wavelet</span> Orthogonal wavelets

The Daubechies wavelets, based on the work of Ingrid Daubechies, are a family of orthogonal wavelets defining a discrete wavelet transform and characterized by a maximal number of vanishing moments for some given support. With each wavelet type of this class, there is a scaling function which generates an orthogonal multiresolution analysis.

In numerical analysis and functional analysis, a discrete wavelet transform (DWT) is any wavelet transform for which the wavelets are discretely sampled. As with other wavelet transforms, a key advantage it has over Fourier transforms is temporal resolution: it captures both frequency and location information.

In signal processing, a filter bank is an array of bandpass filters that separates the input signal into multiple components, each one carrying a sub-band of the original signal. One application of a filter bank is a graphic equalizer, which can attenuate the components differently and recombine them into a modified version of the original signal. The process of decomposition performed by the filter bank is called analysis ; the output of analysis is referred to as a subband signal with as many subbands as there are filters in the filter bank. The reconstruction process is called synthesis, meaning reconstitution of a complete signal resulting from the filtering process.

Originally known as optimal subband tree structuring (SB-TS), also called wavelet packet decomposition, is a wavelet transform where the discrete-time (sampled) signal is passed through more filters than the discrete wavelet transform (DWT).

The stationary wavelet transform (SWT) is a wavelet transform algorithm designed to overcome the lack of translation-invariance of the discrete wavelet transform (DWT). Translation-invariance is achieved by removing the downsamplers and upsamplers in the DWT and upsampling the filter coefficients by a factor of $in the th level of the algorithm. The SWT is an inherently redundant scheme as the output of each level of SWT contains the same number of samples as the input - so for a decomposition of N levels there is a redundancy of N in the wavelet coefficients. This algorithm is more famously known as " algorithme à trous " in French which refers to inserting zeros in the filters. It was introduced by Holschneider et al.$

In mathematics, a wavelet series is a representation of a square-integrable function by a certain orthonormal series generated by a wavelet. This article provides a formal, mathematical definition of an orthonormal wavelet and of the integral wavelet transform.

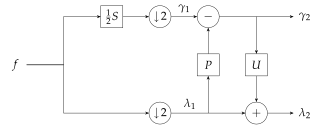
The lifting scheme is a technique for both designing wavelets and performing the discrete wavelet transform (DWT). In an implementation, it is often worthwhile to merge these steps and design the wavelet filters while performing the wavelet transform. This is then called the second-generation wavelet transform. The technique was introduced by Wim Sweldens.

The image fusion process is defined as gathering all the important information from multiple images, and their inclusion into fewer images, usually a single one. This single image is more informative and accurate than any single source image, and it consists of all the necessary information. The purpose of image fusion is not only to reduce the amount of data but also to construct images that are more appropriate and understandable for the human and machine perception. In computer vision, multisensor image fusion is the process of combining relevant information from two or more images into a single image. The resulting image will be more informative than any of the input images.

In image processing, contourlets form a multiresolution directional tight frame designed to efficiently approximate images made of smooth regions separated by smooth boundaries. The contourlet transform has a fast implementation based on a Laplacian pyramid decomposition followed by directional filterbanks applied on each bandpass subband.

<span class="mw-page-title-main">Lie sphere geometry</span> Geometry founded on spheres

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century. The main idea which leads to Lie sphere geometry is that lines should be regarded as circles of infinite radius and that points in the plane should be regarded as circles of zero radius.

Diffusion wavelets are a fast multiscale framework for the analysis of functions on discrete structures like graphs, manifolds, and point clouds in Euclidean space. Diffusion wavelets are an extension of classical wavelet theory from harmonic analysis. Unlike classical wavelets whose basis functions are predetermined, diffusion wavelets are adapted to the geometry of a given diffusion operator $. Moreover, the diffusion wavelet basis functions are constructed by dilation using the dyadic powers of . These dyadic powers of diffusion over the space and propagate local relationships in the function throughout the space until they become global. And if the rank of higher powers of decrease, then these higher powers become compressible. From these decaying dyadic powers of comes a chain of decreasing subspaces. These subspaces are the scaling function approximation subspaces, and the differences in the subspace chain are the wavelet subspaces.$

In mathematics, an invariant convex cone is a closed convex cone in a Lie algebra of a connected Lie group that is invariant under inner automorphisms. The study of such cones was initiated by Ernest Vinberg and Bertram Kostant.

In signal processing it is useful to simultaneously analyze the space and frequency characteristics of a signal. While the Fourier transform gives the frequency information of the signal, it is not localized. This means that we cannot determine which part of a signal produced a particular frequency. It is possible to use a short time Fourier transform for this purpose, however the short time Fourier transform limits the basis functions to be sinusoidal. To provide a more flexible space-frequency signal decomposition several filters have been proposed. The Log-Gabor filter is one such filter that is an improvement upon the original Gabor filter. The advantage of this filter over the many alternatives is that it better fits the statistics of natural images compared with Gabor filters and other wavelet filters.

In computer vision, rigid motion segmentation is the process of separating regions, features, or trajectories from a video sequence into coherent subsets of space and time. These subsets correspond to independent rigidly moving objects in the scene. The goal of this segmentation is to differentiate and extract the meaningful rigid motion from the background and analyze it. Image segmentation techniques labels the pixels to be a part of pixels with certain characteristics at a particular time. Here, the pixels are segmented depending on its relative movement over a period of time i.e. the time of the video sequence.

Dynamic texture is the texture with motion which can be found in videos of sea-waves, fire, smoke, wavy trees, etc. Dynamic texture has a spatially repetitive pattern with time-varying visual pattern. Modeling and analyzing dynamic texture is a topic of images processing and pattern recognition in computer vision.

References

↑ Wu, Jun; Zhao, Zhongming (Mar 2001). "Scale Co-occurrence Matrix for Texture Analysis using Wavelet Transformation". Journal of Remote Sensing. 5 (2): 100.
↑ Duda, R.O. (1973-02-09). Pattern Classification and Scene Analysis . Wiley. ISBN 978-0471223610.
↑ Kevin, Lund; Curt, Burgess (June 1996). "Producing high-dimensional semantic spaces from lexical co-occurrence". Behavior Research Methods. 28 (2): 203–208.
↑ Mallat, S.G. (1989). "A theory for multiresolution signal decomposition: The wavelet representation". IEEE Transactions on Pattern Analysis and Machine Intelligence. 11 (7): 674–693. Bibcode:1989ITPAM..11..674M. doi:10.1109/34.192463.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Wu, Jun; Zhao, Zhongming (Mar 2001). "Scale Co-occurrence Matrix for Texture Analysis using Wavelet Transformation". Journal of Remote Sensing. 5 (2): 100.

[2] Duda, R.O. (1973-02-09). Pattern Classification and Scene Analysis . Wiley. ISBN 978-0471223610.

[3] Kevin, Lund; Curt, Burgess (June 1996). "Producing high-dimensional semantic spaces from lexical co-occurrence". Behavior Research Methods. 28 (2): 203–208.

[4] Mallat, S.G. (1989). "A theory for multiresolution signal decomposition: The wavelet representation". IEEE Transactions on Pattern Analysis and Machine Intelligence. 11 (7): 674–693. Bibcode:1989ITPAM..11..674M. doi:10.1109/34.192463.

[1]

[2]

[3]

[4]