In mathematics, birational geometry is a field of algebraic geometry in which the goal is to determine when two algebraic varieties are isomorphic outside lower-dimensional subsets. This amounts to studying mappings that are given by rational functions rather than polynomials; the map may fail to be defined where the rational functions have poles.
In relation with the history of mathematics, the Italian school of algebraic geometry refers to the work over half a century or more done internationally in birational geometry, particularly on algebraic surfaces. There were in the region of 30 to 40 leading mathematicians who made major contributions, about half of those being in fact Italian. The leadership fell to the group in Rome of Guido Castelnuovo, Federigo Enriques and Francesco Severi, who were involved in some of the deepest discoveries, as well as setting the style.
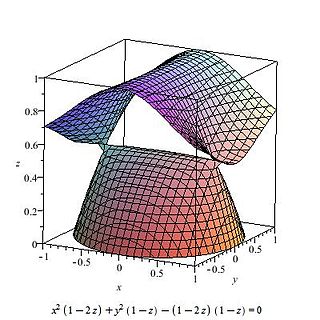
A cubic surface is a projective variety studied in algebraic geometry. It is an algebraic surface in three-dimensional projective space defined by a single quaternary cubic polynomial which is homogeneous of degree 3. Cubic surfaces are del Pezzo surfaces.
In mathematics, a del Pezzo surface or Fano surface is a two-dimensional Fano variety, in other words a non-singular projective algebraic surface with ample anticanonical divisor class. They are in some sense the opposite of surfaces of general type, which have ample canonical class.
In mathematics, the canonical bundle of a non-singular algebraic variety of dimension over a field is the line bundle , which is the nth exterior power of the cotangent bundle Ω on V.
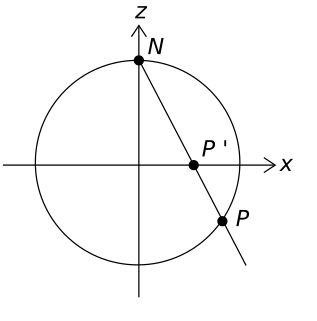
In mathematics, the Segre embedding is used in projective geometry to consider the cartesian product of two projective spaces as a projective variety. It is named after Corrado Segre.

Abramo Giulio Umberto Federigo Enriques was an Italian mathematician, now known principally as the first to give a classification of algebraic surfaces in birational geometry, and other contributions in algebraic geometry.
In algebraic geometry, a branch of mathematics, a rational surface is a surface birationally equivalent to the projective plane, or in other words a rational variety of dimension two. Rational surfaces are the simplest of the 10 or so classes of surface in the Enriques–Kodaira classification of complex surfaces, and were the first surfaces to be investigated.
In mathematics, enumerative geometry is the branch of algebraic geometry concerned with counting numbers of solutions to geometric questions, mainly by means of intersection theory.
In mathematics, Enriques surfaces are algebraic surfaces such that the irregularity q = 0 and the canonical line bundle K is non-trivial but has trivial square. Enriques surfaces are all projective and are elliptic surfaces of genus 0. Over fields of characteristic not 2 they are quotients of K3 surfaces by a group of order 2 acting without fixed points and their theory is similar to that of algebraic K3 surfaces. Enriques surfaces were first studied in detail by Enriques (1896) as an answer to a question discussed by Castelnuovo (1895) about whether a surface with q=pg = 0 is necessarily rational, though some of the Reye congruences introduced earlier by Reye (1882) are also examples of Enriques surfaces.
In algebraic geometry, the Segre cubic is a cubic threefold embedded in 4 dimensional projective space, studied by Corrado Segre (1887).
In algebraic geometry, the Barth–Nieto quintic is a quintic 3-fold in 4 dimensional projective space studied by Barth & Nieto (1994) that is the Hessian of the Segre cubic. The Barth–Nieto quintic is the closure of the set of points (x0:x1:x2:x3:x4:x5) of P5 satisfying the equations
In algebraic geometry, a line complex is a 3-fold given by the intersection of the Grassmannian G(2, 4) with a hypersurface. It is called a line complex because points of G(2, 4) correspond to lines in P3, so a line complex can be thought of as a 3-dimensional family of lines in P3. The linear line complex and quadric line complex are the cases when the hypersurface has degree 1 or 2; they are both rational varieties.
In algebraic geometry, a cubic threefold is a hypersurface of degree 3 in 4-dimensional projective space. Cubic threefolds are all unirational, but Clemens & Griffiths (1972) used intermediate Jacobians to show that non-singular cubic threefolds are not rational. The space of lines on a non-singular cubic 3-fold is a Fano surface.
In algebraic geometry, the Zeuthen–Segre invariantI is an invariant of a projective surface found in a complex projective space which was introduced by Zeuthen (1871) and rediscovered by Corrado Segre (1896).
The terminology of algebraic geometry changed drastically during the twentieth century, with the introduction of the general methods, initiated by David Hilbert and the Italian school of algebraic geometry in the beginning of the century, and later formalized by André Weil, Jean-Pierre Serre and Alexander Grothendieck. Much of the classical terminology, mainly based on case study, was simply abandoned, with the result that books and papers written before this time can be hard to read. This article lists some of this classical terminology, and describes some of the changes in conventions.
Mathematische Annalen is a German mathematical research journal founded in 1868 by Alfred Clebsch and Carl Neumann. Subsequent managing editors were Felix Klein, David Hilbert, Otto Blumenthal, Erich Hecke, Heinrich Behnke, Hans Grauert, Heinz Bauer, Herbert Amann, Jean-Pierre Bourguignon, Wolfgang Lück, and Nigel Hitchin. Currently, the managing editor of Mathematische Annalen is Thomas Schick.

In computing, a Digital Object Identifier orDOI is a persistent identifier or handle used to uniquely identify objects, standardized by the International Organization for Standardization (ISO). An implementation of the Handle System, DOIs are in wide use mainly to identify academic, professional, and government information, such as journal articles, research reports and data sets, and official publications though they also have been used to identify other types of information resources, such as commercial videos.
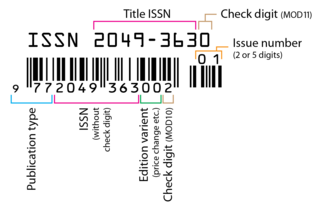
An International Standard Serial Number (ISSN) is an eight-digit serial number used to uniquely identify a serial publication. The ISSN is especially helpful in distinguishing between serials with the same title. ISSN are used in ordering, cataloging, interlibrary loans, and other practices in connection with serial literature.








