Related Research Articles
In logic and computer science, the Boolean satisfiability problem (sometimes called propositional satisfiability problem and abbreviated SATISFIABILITY, SAT or B-SAT) is the problem of determining if there exists an interpretation that satisfies a given Boolean formula. In other words, it asks whether the variables of a given Boolean formula can be consistently replaced by the values TRUE or FALSE in such a way that the formula evaluates to TRUE. If this is the case, the formula is called satisfiable. On the other hand, if no such assignment exists, the function expressed by the formula is FALSE for all possible variable assignments and the formula is unsatisfiable. For example, the formula "a AND NOT b" is satisfiable because one can find the values a = TRUE and b = FALSE, which make (a AND NOT b) = TRUE. In contrast, "a AND NOT a" is unsatisfiable.
The P versus NP problem is a major unsolved problem in theoretical computer science. Informally, it asks whether every problem whose solution can be quickly verified can also be quickly solved.
In theoretical computer science and mathematics, computational complexity theory focuses on classifying computational problems according to their resource usage, and relating these classes to each other. A computational problem is a task solved by a computer. A computation problem is solvable by mechanical application of mathematical steps, such as an algorithm.

In computability theory and computational complexity theory, a decision problem is a computational problem that can be posed as a yes–no question of the input values. An example of a decision problem is deciding by means of an algorithm whether a given natural number is prime. Another is the problem "given two numbers x and y, does x evenly divide y?". The answer is either 'yes' or 'no' depending upon the values of x and y. A method for solving a decision problem, given in the form of an algorithm, is called a decision procedure for that problem. A decision procedure for the decision problem "given two numbers x and y, does x evenly divide y?" would give the steps for determining whether x evenly divides y. One such algorithm is long division. If the remainder is zero the answer is 'yes', otherwise it is 'no'. A decision problem which can be solved by an algorithm is called decidable.

In computational complexity theory, NP is a complexity class used to classify decision problems. NP is the set of decision problems for which the problem instances, where the answer is "yes", have proofs verifiable in polynomial time by a deterministic Turing machine, or alternatively the set of problems that can be solved in polynomial time by a nondeterministic Turing machine.
In theoretical computer science and formal language theory, a regular language is a formal language that can be defined by a regular expression, in the strict sense in theoretical computer science.

In theoretical computer science and mathematics, the theory of computation is the branch that deals with what problems can be solved on a model of computation, using an algorithm, how efficiently they can be solved or to what degree. The field is divided into three major branches: automata theory and formal languages, computability theory, and computational complexity theory, which are linked by the question: "What are the fundamental capabilities and limitations of computers?".
In computational complexity theory, randomized polynomial time (RP) is the complexity class of problems for which a probabilistic Turing machine exists with these properties:

Combinatorial optimization is a subfield of mathematical optimization that consists of finding an optimal object from a finite set of objects, where the set of feasible solutions is discrete or can be reduced to a discrete set. Typical combinatorial optimization problems are the travelling salesman problem ("TSP"), the minimum spanning tree problem ("MST"), and the knapsack problem. In many such problems, such as the ones previously mentioned, exhaustive search is not tractable, and so specialized algorithms that quickly rule out large parts of the search space or approximation algorithms must be resorted to instead.

In computational complexity theory, a complexity class is a set of computational problems "of related resource-based complexity". The two most commonly analyzed resources are time and memory.
In computer science, parameterized complexity is a branch of computational complexity theory that focuses on classifying computational problems according to their inherent difficulty with respect to multiple parameters of the input or output. The complexity of a problem is then measured as a function of those parameters. This allows the classification of NP-hard problems on a finer scale than in the classical setting, where the complexity of a problem is only measured as a function of the number of bits in the input. This appears to have been first demonstrated in Gurevich, Stockmeyer & Vishkin (1984). The first systematic work on parameterized complexity was done by Downey & Fellows (1999).

In computational complexity theory, the complexity class PH is the union of all complexity classes in the polynomial hierarchy:
In computational complexity theory, the polynomial hierarchy is a hierarchy of complexity classes that generalize the classes NP and co-NP. Each class in the hierarchy is contained within PSPACE. The hierarchy can be defined using oracle machines or alternating Turing machines. It is a resource-bounded counterpart to the arithmetical hierarchy and analytical hierarchy from mathematical logic. The union of the classes in the hierarchy is denoted PH.
In computer science, the shortest common supersequence of two sequences X and Y is the shortest sequence which has X and Y as subsequences. This is a problem closely related to the longest common subsequence problem. Given two sequences X = < x1,...,xm > and Y = < y1,...,yn >, a sequence U = < u1,...,uk > is a common supersequence of X and Y if items can be removed from U to produce X and Y.
In logic and theoretical computer science, and specifically proof theory and computational complexity theory, proof complexity is the field aiming to understand and analyse the computational resources that are required to prove or refute statements. Research in proof complexity is predominantly concerned with proving proof-length lower and upper bounds in various propositional proof systems. For example, among the major challenges of proof complexity is showing that the Frege system, the usual propositional calculus, does not admit polynomial-size proofs of all tautologies. Here the size of the proof is simply the number of symbols in it, and a proof is said to be of polynomial size if it is polynomial in the size of the tautology it proves.
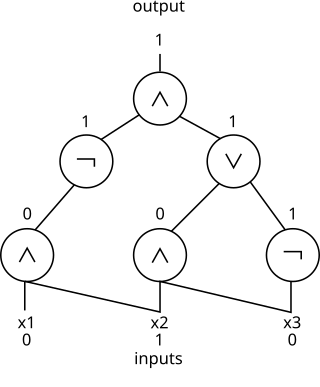
In theoretical computer science, circuit complexity is a branch of computational complexity theory in which Boolean functions are classified according to the size or depth of the Boolean circuits that compute them. A related notion is the circuit complexity of a recursive language that is decided by a uniform family of circuits .
In computational complexity theory, the average-case complexity of an algorithm is the amount of some computational resource used by the algorithm, averaged over all possible inputs. It is frequently contrasted with worst-case complexity which considers the maximal complexity of the algorithm over all possible inputs.
In theoretical computer science, the term isolation lemma refers to randomized algorithms that reduce the number of solutions to a problem to one, should a solution exist. This is achieved by constructing random constraints such that, with non-negligible probability, exactly one solution satisfies these additional constraints if the solution space is not empty. Isolation lemmas have important applications in computer science, such as the Valiant–Vazirani theorem and Toda's theorem in computational complexity theory.
In structural complexity theory, the Berman–Hartmanis conjecture is an unsolved conjecture named after Leonard C. Berman and Juris Hartmanis that states that all NP-complete languages look alike, in the sense that they can be related to each other by polynomial time isomorphisms.
References
- Derek Denny-Brown, "Semi-membership algorithms: some recent advances", Technical report, University of Rochester Dept. of Computer Science, 1994
- Lane A. Hemaspaandra, Mitsunori Ogihara, "The complexity theory companion", Texts in theoretical computer science, EATCS series, Springer, 2002, ISBN 3-540-67419-5, page 294
- Lane A. Hemaspaandra, Leen Torenvliet, "Theory of semi-feasible algorithms", Monographs in theoretical computer science, Springer, 2003, ISBN 3-540-42200-5, page 1
- Ker-I Ko, "Applying techniques of discrete complexity theory to numerical computation" in Ronald V. Book (ed.), "Studies in complexity theory", Research notes in theoretical computer science, Pitman, 1986, ISBN 0-470-20293-9, p. 40
- C. Jockusch jr (1968). "Semirecursive sets and positive reducibility" (PDF). Trans. Amer. Math. Soc. 137: 420–436.