Related Research Articles

The Rubik's Cube is a 3-D combination puzzle originally invented in 1974 by Hungarian sculptor and professor of architecture Ernő Rubik. Originally called the Magic Cube, the puzzle was licensed by Rubik to be sold by Ideal Toy Corp in 1980 via businessman Tibor Laczi and Seven Towns founder Tom Kremer. The cube was released internationally in 1980 and became one of the most recognized icons in popular culture. It won the 1980 German Game of the Year special award for Best Puzzle. As of January 2009, 350 million cubes had been sold worldwide, making it the world's bestselling puzzle game and bestselling toy.

Ernő Rubik is a Hungarian inventor, architect and professor of architecture. He is best known for the invention of mechanical puzzles including the Rubik's Cube (1974), Rubik's Magic, Rubik's Magic: Master Edition, and Rubik's Snake.

Rubik's Magic, like the Rubik's Cube, is a mechanical puzzle invented by Ernő Rubik and first manufactured by Matchbox in the mid-1980s.
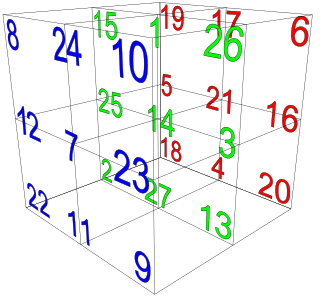
In mathematics, a magic cube is the 3-dimensional equivalent of a magic square, that is, a collection of integers arranged in an n × n × n pattern such that the sums of the numbers on each row, on each column, on each pillar and on each of the four main space diagonals are equal to the same number, the so-called magic constant of the cube, denoted M3(n). It can be shown that if a magic cube consists of the numbers 1, 2, ..., n3, then it has magic constant
In mathematics, a perfect magic cube is a magic cube in which not only the columns, rows, pillars, and main space diagonals, but also the cross section diagonals sum up to the cube's magic constant.
In mathematics, a P-multimagic cube is a magic cube that remains magic even if all its numbers are replaced by their k th powers for 1 ≤ k ≤ P. 2-multimagic cubes are called bimagic, 3-multimagic cubes are called trimagic, and 4-multimagic cubes tetramagic. A P-multimagic cube is said to be semi-perfect if the k th power cubes are perfect for 1 ≤ k < P, and the P th power cube is semiperfect. If all P of the power cubes are perfect, the P-multimagic cube is said to be perfect.
In mathematics, a P-multimagic square is a magic square that remains magic even if all its numbers are replaced by their kth powers for 1 ≤ k ≤ P. 2-multimagic squares are called bimagic, 3-multimagic squares are called trimagic, 4-multimagic squares tetramagic, and 5-multimagic squares pentamagic.
In mathematics, a magic hypercube is the k-dimensional generalization of magic squares and magic cubes, that is, an n × n × n × ... × n array of integers such that the sums of the numbers on each pillar as well as on the main space diagonals are all the same. The common sum is called the magic constant of the hypercube, and is sometimes denoted Mk(n). If a magic hypercube consists of the numbers 1, 2, ..., nk, then it has magic number

David Breyer Singmaster is an emeritus professor of mathematics at London South Bank University, England. A self-described metagrobologist, he has a huge personal collection of mechanical puzzles and books of brain teasers. He is most famous for being an early adopter and enthusiastic promoter of the Rubik's Cube. His Notes on Rubik's "Magic Cube" which he began compiling in 1979 provided the first mathematical analysis of the Cube as well as providing one of the first published solutions. The book contained his cube notation which allowed the recording of Rubik's Cube moves, and which quickly became the standard.

In geometry, a space diagonal of a polyhedron is a line connecting two vertices that are not on the same face. Space diagonals contrast with face diagonals, which connect vertices on the same face as each other.
Every magic cube may be assigned to one of six magic cube classes, based on the cube characteristics.
In recreational mathematics, a pandiagonal magic cube is a magic cube with the additional property that all broken diagonals have the same sum as each other. Pandiagonal magic cubes are extensions of diagonal magic cubes and generalize pandiagonal magic squares to three dimensions.

"Go to Church" is the second official single from Ice Cube's album Laugh Now, Cry Later. The song features Snoop Dogg and Lil Jon. The song is also produced by Lil Jon and a music video was released for the song. In the edited version, instead of "mothafucka," Ice Cube says "mothamotha".
Bob Burton is an American speedcuber, most famous for competing in and organizing competitions all over the world and his former world records on the Rubik's Magic and Rubik's Master Magic.

Cube with Magic Ribbons is a lithograph print by the Dutch artist M. C. Escher first printed in 1957. It depicts two interlocking bands wrapped around the frame of a Necker cube. The bands have what Escher called small "nodules" or "buttonlike protuberances" that make use of the dome/crater illusion, an optical illusion characterized by shifting perception of depth from concave to convex depending on direction of light and shadow. Escher's interest in reversible perspectives, as seen in Cube with Magic Ribbons, can also be noted in an earlier work, Convex and Concave, first printed in 1955.

A combination puzzle, also known as a sequential move puzzle, is a puzzle which consists of a set of pieces which can be manipulated into different combinations by a group of operations. Many such puzzles are mechanical puzzles of polyhedral shape, consisting of multiple layers of pieces along each axis which can rotate independently of each other. Collectively known as twisty puzzles, the archetype of this kind of puzzle is the Rubik's Cube. Each rotating side is usually marked with different colours, intended to be scrambled, then 'solved' by a sequence of moves that sort the facets by colour. As a generalisation, combination puzzles also include mathematically defined examples that have not been, or are impossible to, physically construct.

The Rubik's Cube is the original and best known of the three-dimensional sequential move puzzles. There have been many virtual implementations of this puzzle in software. It is a natural extension to create sequential move puzzles in more than three dimensions. Although no such puzzle could ever be physically constructed, the rules of how they operate are quite rigorously defined mathematically and are analogous to the rules found in three-dimensional geometry. Hence, they can be simulated by software. As with the mechanical sequential move puzzles, there are records for solvers, although not yet the same degree of competitive organisation.

Conversations with Magic Stones is a public art work by English artist Barbara Hepworth located at the Lynden Sculpture Garden near Milwaukee, Wisconsin. The sculpture is an abstract, modified cube form made of bronze; it is installed on the lawn. Originally, this work was created as part of a multi-part sculpture with two other bronze "magic stones" and three "figures". One of these other works, Conversations with Magic Stones , is also installed at the Lynden Sculpture Garden.
The Layer by Layer method, also known as the Beginners method is a method of solving the 3x3x3 Rubik's Cube. Many beginners' methods use this approach, and it also forms the basis of the CFOP speedcubing technique.
References
- Pickover, Clifford A. (2003), The Zen of Magic Squares, Circles, and Stars: An Exhibition of Surprising Structures across Dimensions, Princeton University Press, p. 98, ISBN 1400841518 .