Related Research Articles

Soil liquefaction occurs when a cohesionless saturated or partially saturated soil substantially loses strength and stiffness in response to an applied stress such as shaking during an earthquake or other sudden change in stress condition, in which material that is ordinarily a solid behaves like a liquid. In soil mechanics, the term "liquefied" was first used by Allen Hazen in reference to the 1918 failure of the Calaveras Dam in California. He described the mechanism of flow liquefaction of the embankment dam as:
If the pressure of the water in the pores is great enough to carry all the load, it will have the effect of holding the particles apart and of producing a condition that is practically equivalent to that of quicksand... the initial movement of some part of the material might result in accumulating pressure, first on one point, and then on another, successively, as the early points of concentration were liquefied.

Soil mechanics is a branch of soil physics and applied mechanics that describes the behavior of soils. It differs from fluid mechanics and solid mechanics in the sense that soils consist of a heterogeneous mixture of fluids and particles but soil may also contain organic solids and other matter. Along with rock mechanics, soil mechanics provides the theoretical basis for analysis in geotechnical engineering, a subdiscipline of civil engineering, and engineering geology, a subdiscipline of geology. Soil mechanics is used to analyze the deformations of and flow of fluids within natural and man-made structures that are supported on or made of soil, or structures that are buried in soils. Example applications are building and bridge foundations, retaining walls, dams, and buried pipeline systems. Principles of soil mechanics are also used in related disciplines such as geophysical engineering, coastal engineering, agricultural engineering, hydrology and soil physics.

Slope stability refers to the condition of inclined soil or rock slopes to withstand or undergo movement; the opposite condition is called slope instability or slope failure. The stability condition of slopes is a subject of study and research in soil mechanics, geotechnical engineering and engineering geology. Analyses are generally aimed at understanding the causes of an occurred slope failure, or the factors that can potentially trigger a slope movement, resulting in a landslide, as well as at preventing the initiation of such movement, slowing it down or arresting it through mitigation countermeasures.
Rock mass classification systems are used for various engineering design and stability analysis. These are based on empirical relations between rock mass parameters and engineering applications, such as tunnels, slopes, foundations, and excavatability. The first rock mass classification system in geotechnical engineering was proposed in 1946 for tunnels with steel set support.

Rock mechanics is a theoretical and applied science of the mechanical behavior of rocks and rock masses.
Geomechanics is the study of the mechanical state of the Earth's crust and the processes occurring in it under the influence of natural physical factors. It involves the study of the mechanics of soil and rock.
A direct shear test is a laboratory or field test used by geotechnical engineers to measure the shear strength properties of soil or rock material, or of discontinuities in soil or rock masses.

A fracture is any separation in a geologic formation, such as a joint or a fault that divides the rock into two or more pieces. A fracture will sometimes form a deep fissure or crevice in the rock. Fractures are commonly caused by stress exceeding the rock strength, causing the rock to lose cohesion along its weakest plane. Fractures can provide permeability for fluid movement, such as water or hydrocarbons. Highly fractured rocks can make good aquifers or hydrocarbon reservoirs, since they may possess both significant permeability and fracture porosity.

A triaxial shear test is a common method to measure the mechanical properties of many deformable solids, especially soil and rock, and other granular materials or powders. There are several variations on the test.

Shear strength is a term used in soil mechanics to describe the magnitude of the shear stress that a soil can sustain. The shear resistance of soil is a result of friction and interlocking of particles, and possibly cementation or bonding of particle contacts. Due to interlocking, particulate material may expand or contract in volume as it is subject to shear strains. If soil expands its volume, the density of particles will decrease and the strength will decrease; in this case, the peak strength would be followed by a reduction of shear stress. The stress-strain relationship levels off when the material stops expanding or contracting, and when interparticle bonds are broken. The theoretical state at which the shear stress and density remain constant while the shear strain increases may be called the critical state, steady state, or residual strength.
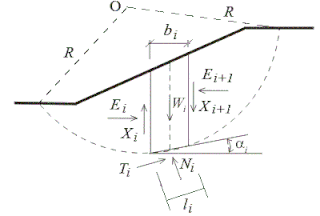
Slope stability analysis is a static or dynamic, analytical or empirical method to evaluate the stability of slopes of soil- and rock-fill dams, embankments, excavated slopes, and natural slopes in soil and rock. It is performed to assess the safe design of a human-made or natural slopes and the equilibrium conditions. Slope stability is the resistance of inclined surface to failure by sliding or collapsing. The main objectives of slope stability analysis are finding endangered areas, investigation of potential failure mechanisms, determination of the slope sensitivity to different triggering mechanisms, designing of optimal slopes with regard to safety, reliability and economics, designing possible remedial measures, e.g. barriers and stabilization.
The Geological Strength Index (GSI) system, proposed in 1994 by Evert Hoek, is used for the estimation of the rock mass strength and the rock mass deformation modulus.
A discontinuity in geotechnical engineering is a plane or surface that marks a change in physical or chemical characteristics in a soil or rock mass. A discontinuity can be, for example, a bedding, schistosity, foliation, joint, cleavage, fracture, fissure, crack, or fault plane. A division is made between mechanical and integral discontinuities. Discontinuities may occur multiple times with broadly the same mechanical characteristics in a discontinuity set, or may be a single discontinuity. A discontinuity makes a soil or rock mass anisotropic.
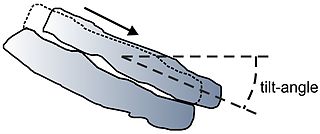
In geomechanics, a tilt test is a simple test to estimate the shear strength parameters of a discontinuity. Two pieces of rock containing a discontinuity are held in hand or mounted in test equipment with the discontinuity horizontal. The sample is slowly tilted until the top block moves. The angle with the horizontal at onset of movement is called the tilt-angle.
In geotechnical engineering and contact mechanics the term asperity is used to refer to individual features of unevenness (roughness) of the surface of a discontinuity, grain, or particle with heights in the range from approximately 0.1 mm to the order of metres. Below the asperity level, surface interactions are normally considered to be a material property, arising from mechanisms of adhesion and repulsion at the atomic scale.
The rock mass rating (RMR) is a geomechanical classification system for rocks, developed by Z. T. Bieniawski between 1972 and 1973. Since then it has undergone multiple modifications out of which, RMR89 is commonly used. Recently RMR14 has been proposed to improve the RMR performance by incorporating new experiences from tunnel practices. Continuous functions and a software "QuickRMR" for RMR89 and RMR14 have also been proposed by Kundu. RMR combines the most significant geologic parameters of influence and represents them with one overall comprehensive index of rock mass quality, which is used for the design and construction of excavations in rock, such as tunnels, mines, slopes, and foundations.
The Q-system for rock mass classification is developed by Barton, Lien, and Lunde. It expresses the quality of the rock mass in the so-called Q-value, on which design are based and support recommendations for underground excavations.

Persistence determines the possibilities of relative movement along a discontinuity in a soil or rock mass in geotechnical engineering. Discontinuities are usually differentiated in persistent, non-persistent, and abutting discontinuities (figure).
The sliding criterion (discontinuity) is a tool to estimate easily the shear strength properties of a discontinuity in a rock mass based on visual and tactile characterization of the discontinuity. The shear strength of a discontinuity is important in, for example, tunnel, foundation, or slope engineering, but also stability of natural slopes is often governed by the shear strength along discontinuities.
In soil mechanics, dilatancy is the volume change observed in granular materials when they are subjected to shear deformations. This effect was first described scientifically by Osborne Reynolds in 1885/1886 and is also known as Reynolds dilatancy. It was brought into the field of geotechnical engineering by Peter Walter Rowe.
References
- ↑ Hoek, E.; Bray, J. (1974). Rock slope engineering. London: Institute of Mining and Metallurgy. pp. 358. ISBN 978-0-419-16010-6.
- ↑ Hoek, E.; Brown, E.T. (1990). Underground excavations in rock. London: Institute of Mining and Metallurgy; Spon Press, Taylor & Francis. p. 536. ISBN 978-0-419-16030-4.
- ↑ Hack, R. (1998). Slope Stability Probability Classification (SSPC) (PDF). ITC publication 43 (2nd ed.). Technical University Delft & Twente University - International Institute for Aerospace Survey and Earth Sciences (ITC Enschede), Netherlands. p. 258. ISBN 90-6164-154-3.
- 1 2 ISRM (2007). Ulusay, R.; Hudson, J.A. (eds.). The Blue Book - The Complete ISRM Suggested Methods for Rock Characterization, Testing and Monitoring: 1974-2006. Ankara: ISRM & ISRM Turkish National Group. p. 628. ISBN 978-975-93675-4-1.
- 1 2 Price, D.G. (2009). De Freitas, M.H. (ed.). Engineering Geology: Principles and Practice. Springer. p. 450. ISBN 978-3-540-29249-4.
- ↑ Hencher, S.R.; Lee, S.G.; Carter, T.G.; Richards, L.R. (2011). "Sheeting Joints: Characterisation, Shear Strength and Engineering". Rock Mechanics and Rock Engineering. 44 (1): 1–22. Bibcode:2011RMRE...44....1H. doi: 10.1007/s00603-010-0100-y .
- ↑ Gaziev, E.; Erlikhman, S. (4–6 October 1971). Stresses and strains in anisotropic foundations. Rock fracture: proceedings of the International Symposium on Rock Mechanics ISRM. Nancy, France: École Nationale Supérieure de Géologie Appliquée et de Prospection Minière : École Nationale Supérieure de la Métallurgie et de l'Industrie des Mines, Rubrecht, Nancy. pp. 11–1.
- 1 2 Patton, F.D. (25 Sep – 1 Oct 1966). Rocha, M. (ed.). Multiple Modes of Shear Failure in Rock. Proc. 1st Congress of International Society for Rock Mechanics (ISRM). Vol. 1. Lisbon, Portugal: Laboratório Nacional de Engenharia Civil, Lisboa, Portugal. pp. 509–513. OL 19662608M.
- ↑ Rengers, N. (1970). Influence of surface roughness on the friction properties of rock planes. Proceedings 2nd International Congress on Rock Mechanics, ISRM, Belgrade. Vol. 1. ISRM. pp. 229–234.
- ↑ Fecker, E.; Rengers, N. (1971). Measurement of large scale roughness of rock planes by means of profilograph and geological compass. Proceedings symposium on rock fracture, Nancy, France. pp. 1–18.
- 1 2 Hencher, S. R.; Richards, L. R. (1989). "Laboratory direct shear testing of rock discontinuities". Ground Engineering. 22 (2): 24–31.
- 1 2 3 Barton, N.R.; Bandis, S.C. (4–6 June 1990). Barton, N.; Stephansson, O. (eds.). Review of predictive capabilities of JRC-JCS model in engineering practice. Rock Joints: Regional Conference of the International Society for Rock Mechanics ISRM. Loen, Norway: Balkema, Rotterdam, Taylor & Francis. pp. 603–610. ISBN 978-90-6191-109-8.
- ↑ Phien-wej, N.; Shrestha, U.B.; Rantucci, G. (1990). Barton, N.R.; Stephansson, O. (eds.). Effect of infill thickness on shear behaviour of rock joints. Rock Joints. Balkema (Taylor & Francis), Rotterdam. pp. 289–294. ISBN 978-90-6191-109-8.
- 1 2 Shemirani, Alireza Bagher; Sarfarazi, Vahab; Haeri, Hari; Marji, Mohammad Fatehi; Hosseini, Seyed shahin (2018). "A discrete element simulation of a punch-through shear test to investigate the confining pressure effects on the shear behaviour of concrete cracks". Computers and Concrete. 21 (2): 189–197. doi:10.12989/cac.2018.21.2.189.
- 1 2 Hack, H.R.G.K.; Price, D.G. (September 25–29, 1995). Fujii, T. (ed.). Determination of discontinuity friction by rock mass classification (PDF). Proceedings 8th International Society for Rock Mechanics (ISRM) congress. Vol. 3. Tokyo, Japan: Balkema, Rotterdam, Taylor & Francis. pp. 23–27. ISBN 978-90-5410-576-3.