
Dijkstra's algorithm is an algorithm for finding the shortest paths between nodes in a weighted graph, which may represent, for example, road networks. It was conceived by computer scientist Edsger W. Dijkstra in 1956 and published three years later.
This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.

In the mathematical field of graph theory, a spanning treeT of an undirected graph G is a subgraph that is a tree which includes all of the vertices of G. In general, a graph may have several spanning trees, but a graph that is not connected will not contain a spanning tree. If all of the edges of G are also edges of a spanning tree T of G, then G is a tree and is identical to T.

In combinatorial mathematics, the Steiner tree problem, or minimum Steiner tree problem, named after Jakob Steiner, is an umbrella term for a class of problems in combinatorial optimization. While Steiner tree problems may be formulated in a number of settings, they all require an optimal interconnect for a given set of objects and a predefined objective function. One well-known variant, which is often used synonymously with the term Steiner tree problem, is the Steiner tree problem in graphs. Given an undirected graph with non-negative edge weights and a subset of vertices, usually referred to as terminals, the Steiner tree problem in graphs requires a tree of minimum weight that contains all terminals and minimizes the total weight of its edges. Further well-known variants are the Euclidean Steiner tree problem and the rectilinear minimum Steiner tree problem.
In mathematics, computer science and especially graph theory, a distance matrix is a square matrix containing the distances, taken pairwise, between the elements of a set. Depending upon the application involved, the distance being used to define this matrix may or may not be a metric. If there are N elements, this matrix will have size N×N. In graph-theoretic applications, the elements are more often referred to as points, nodes or vertices.

A Euclidean minimum spanning tree of a finite set of points in the Euclidean plane or higher-dimensional Euclidean space connects the points by a system of line segments with the points as endpoints, minimizing the total length of the segments. In it, any two points can reach each other along a path through the line segments. It can be found as the minimum spanning tree of a complete graph with the points as vertices and the Euclidean distances between points as edge weights.
In the mathematical field of graph theory, an induced subgraph of a graph is another graph, formed from a subset of the vertices of the graph and all of the edges connecting pairs of vertices in that subset.
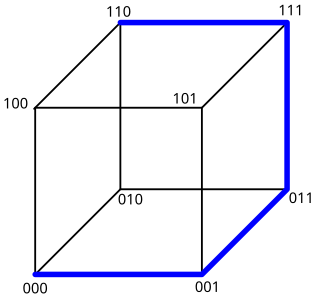
In the mathematical area of graph theory, an induced path in an undirected graph G is a path that is an induced subgraph of G. That is, it is a sequence of vertices in G such that each two adjacent vertices in the sequence are connected by an edge in G, and each two nonadjacent vertices in the sequence are not connected by any edge in G. An induced path is sometimes called a snake, and the problem of finding long induced paths in hypercube graphs is known as the snake-in-the-box problem.
A geometric spanner or a t-spanner graph or a t-spanner was initially introduced as a weighted graph over a set of points as its vertices for which there is a t-path between any pair of vertices for a fixed parameter t. A t-path is defined as a path through the graph with weight at most t times the spatial distance between its endpoints. The parameter t is called the stretch factor or dilation factor of the spanner.

The nearest neighbor graph (NNG) is a directed graph defined for a set of points in a metric space, such as the Euclidean distance in the plane. The NNG has a vertex for each point, and a directed edge from p to q whenever q is a nearest neighbor of p, a point whose distance from p is minimum among all the given points other than p itself.
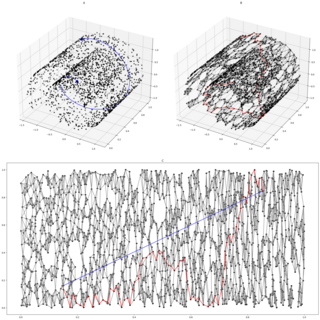
Isomap is a nonlinear dimensionality reduction method. It is one of several widely used low-dimensional embedding methods. Isomap is used for computing a quasi-isometric, low-dimensional embedding of a set of high-dimensional data points. The algorithm provides a simple method for estimating the intrinsic geometry of a data manifold based on a rough estimate of each data point’s neighbors on the manifold. Isomap is highly efficient and generally applicable to a broad range of data sources and dimensionalities.

In graph theory, a division of mathematics, a median graph is an undirected graph in which every three vertices a, b, and c have a unique median: a vertex m(a,b,c) that belongs to shortest paths between each pair of a, b, and c.
In computer science and graph theory, the Canadian traveller problem (CTP) is a generalization of the shortest path problem to graphs that are partially observable. In other words, a "traveller" on a given point on the graph cannot see the full graph, rather only adjacent nodes or a certain "realization restriction."

In graph theory, a branch of mathematics, a cycle basis of an undirected graph is a set of simple cycles that forms a basis of the cycle space of the graph. That is, it is a minimal set of cycles that allows every even-degree subgraph to be expressed as a symmetric difference of basis cycles.
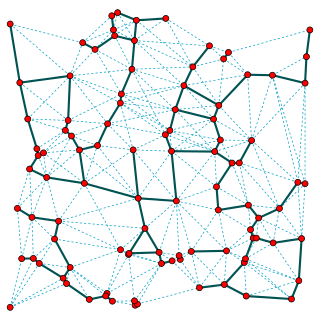
In computational geometry and geometric graph theory, a β-skeleton or beta skeleton is an undirected graph defined from a set of points in the Euclidean plane. Two points p and q are connected by an edge whenever all the angles prq are sharper than a threshold determined from the numerical parameter β.
In theoretical computer science and network routing, Suurballe's algorithm is an algorithm for finding two disjoint paths in a nonnegatively-weighted directed graph, so that both paths connect the same pair of vertices and have minimum total length. The algorithm was conceived by John W. Suurballe and published in 1974. The main idea of Suurballe's algorithm is to use Dijkstra's algorithm to find one path, to modify the weights of the graph edges, and then to run Dijkstra's algorithm a second time. The output of the algorithm is formed by combining these two paths, discarding edges that are traversed in opposite directions by the paths, and using the remaining edges to form the two paths to return as the output. The modification to the weights is similar to the weight modification in Johnson's algorithm, and preserves the non-negativity of the weights while allowing the second instance of Dijkstra's algorithm to find the correct second path.

In graph algorithms, the widest path problem is the problem of finding a path between two designated vertices in a weighted graph, maximizing the weight of the minimum-weight edge in the path. The widest path problem is also known as the maximum capacity path problem. It is possible to adapt most shortest path algorithms to compute widest paths, by modifying them to use the bottleneck distance instead of path length. However, in many cases even faster algorithms are possible.
In mathematics, a minimum bottleneck spanning tree (MBST) in an undirected graph is a spanning tree in which the most expensive edge is as cheap as possible. A bottleneck edge is the highest weighted edge in a spanning tree. A spanning tree is a minimum bottleneck spanning tree if the graph does not contain a spanning tree with a smaller bottleneck edge weight. For a directed graph, a similar problem is known as Minimum Bottleneck Spanning Arborescence (MBSA).
In the mathematical field of graph theory, planarization is a method of extending graph drawing methods from planar graphs to graphs that are not planar, by embedding the non-planar graphs within a larger planar graph.
In network theory, the Wiener connector is a means of maximizing efficiency in connecting specified "query vertices" in a network. Given a connected, undirected graph and a set of query vertices in a graph, the minimum Wiener connector is an induced subgraph that connects the query vertices and minimizes the sum of shortest path distances among all pairs of vertices in the subgraph. In combinatorial optimization, the minimum Wiener connector problem is the problem of finding the minimum Wiener connector. It can be thought of as a version of the classic Steiner tree problem, where instead of minimizing the size of the tree, the objective is to minimize the distances in the subgraph.











