In mathematics, a modular form is a (complex) analytic function on the upper half-plane satisfying a certain kind of functional equation with respect to the group action of the modular group, and also satisfying a growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections with number theory. Modular forms appear in other areas, such as algebraic topology, sphere packing, and string theory.
In differential geometry, the Atiyah–Singer index theorem, proved by Michael Atiyah and Isadore Singer (1963), states that for an elliptic differential operator on a compact manifold, the analytical index is equal to the topological index. It includes many other theorems, such as the Riemann–Roch theorem, as special cases, and has applications in theoretical physics.

Sir Simon Kirwan Donaldson FRS, is an English mathematician known for his work on the topology of smooth (differentiable) four-dimensional manifolds and Donaldson–Thomas theory. He is currently a permanent member of the Simons Center for Geometry and Physics at Stony Brook University and a Professor in Pure Mathematics at Imperial College London.
In mathematics, the Selberg trace formula, introduced by Selberg (1956), is an expression for the character of the unitary representation of G on the space L2(G/Γ) of square-integrable functions, where G is a Lie group and Γ a cofinite discrete group. The character is given by the trace of certain functions on G.

Friedrich Ernst Peter Hirzebruch ForMemRS was a German mathematician, working in the fields of topology, complex manifolds and algebraic geometry, and a leading figure in his generation. He has been described as "the most important mathematician in Germany of the postwar period."

Don Bernard Zagier is an American mathematician whose main area of work is number theory. He is currently one of the directors of the Max Planck Institute for Mathematics in Bonn, Germany. He was a professor at the Collège de France in Paris, France from 2006 to 2014. Since October 2014, he is also a Distinguished Staff Associate at ICTP.
In mathematics, vector bundles on algebraic curves may be studied as holomorphic vector bundles on compact Riemann surfaces. which is the classical approach, or as locally free sheaves on algebraic curves C in a more general, algebraic setting.
In 4-dimensional topology, a branch of mathematics, Rokhlin's theorem states that if a smooth, closed 4-manifold M has a spin structure, then the signature of its intersection form, a quadratic form on the second cohomology group , is divisible by 16. The theorem is named for Vladimir Rokhlin, who proved it in 1952.
In mathematics, Harish-Chandra's regularity theorem, introduced by Harish-Chandra (1963), states that every invariant eigendistribution on a semisimple Lie group, and in particular every character of an irreducible unitary representation on a Hilbert space, is given by a locally integrable function. Harish-Chandra proved a similar theorem for semisimple p-adic groups.
In mathematics, a stable vector bundle is a vector bundle that is stable in the sense of geometric invariant theory. Any holomorphic vector bundle may be built from stable ones using Harder-Narasimhan filtration. Stable bundles were defined by David Mumford in Mumford (1963) and later built upon by David Gieseker, Fedor Bogomolov, Thomas Bridgeland and many others.
In mathematics, the signature operator is an elliptic differential operator defined on a certain subspace of the space of differential forms on an even-dimensional compact Riemannian manifold, whose analytic index is the same as the topological signature of the manifold if the dimension of the manifold is a multiple of four. It is an instance of a Dirac-type operator.

In mathematics, the Clebsch diagonal cubic surface, or Klein's icosahedral cubic surface, is a non-singular cubic surface, studied by Clebsch (1871) and Klein (1873), all of whose 27 exceptional lines can be defined over the real numbers. The term Klein's icosahedral surface can refer to either this surface or its blowup at the 10 Eckardt points.
In mathematics, the Doi–Naganuma lifting is a map from elliptic modular forms to Hilbert modular forms of a real quadratic field, introduced by Doi & Naganuma (1969) and Naganuma (1973). It was a precursor of the base change lifting.
In mathematics, the eta invariant of a self-adjoint elliptic differential operator on a compact manifold is formally the number of positive eigenvalues minus the number of negative eigenvalues. In practice both numbers are often infinite so are defined using zeta function regularization. It was introduced by Atiyah, Patodi, and Singer who used it to extend the Hirzebruch signature theorem to manifolds with boundary. The name comes from the fact that it is a generalization of the Dirichlet eta function.
In mathematics, the Shimizu L-function, introduced by Hideo Shimizu (1963), is a Dirichlet series associated to a totally real algebraic number field. Michael Francis Atiyah, H. Donnelly, and I. M. Singer (1983) defined the signature defect of the boundary of a manifold as the eta invariant, the value as s=0 of their eta function, and used this to show that Hirzebruch's signature defect of a cusp of a Hilbert modular surface can be expressed in terms of the value at s=0 or 1 of a Shimizu L-function.
Hideo Shimizu is a Japanese mathematician who introduced Shimizu L-functions.
In mathematics, the Meyer signature cocyle, introduced by Meyer (1973). is an integer-valued 2-cocyle on a symplectic group that describes the signature of a fiber bundle whose base and fiber are both Riemann surfaces.
The Annals of Mathematics is a bimonthly mathematical journal published by Princeton University and the Institute for Advanced Study.

In computing, a Digital Object Identifier orDOI is a persistent identifier or handle used to uniquely identify objects, standardized by the International Organization for Standardization (ISO). An implementation of the Handle System, DOIs are in wide use mainly to identify academic, professional, and government information, such as journal articles, research reports and data sets, and official publications though they also have been used to identify other types of information resources, such as commercial videos.
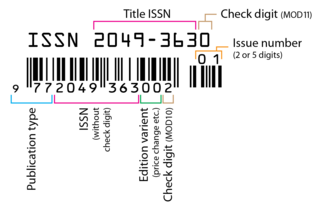
An International Standard Serial Number (ISSN) is an eight-digit serial number used to uniquely identify a serial publication. The ISSN is especially helpful in distinguishing between serials with the same title. ISSN are used in ordering, cataloging, interlibrary loans, and other practices in connection with serial literature.







