In mathematics, and in particular game theory, Sion's minimax theorem is a generalization of John von Neumann's minimax theorem, named after Maurice Sion.
It states:
Let be a compact convex subset of a linear topological space and a convex subset of a linear topological space. If is a real-valued function on with
then,
In mathematics, more specifically in functional analysis, a Banach space is a complete normed vector space. Thus, a Banach space is a vector space with a metric that allows the computation of vector length and distance between vectors and is complete in the sense that a Cauchy sequence of vectors always converges to a well-defined limit that is within the space.
The Hahn–Banach theorem is a central tool in functional analysis. It allows the extension of bounded linear functionals defined on a subspace of some vector space to the whole space, and it also shows that there are "enough" continuous linear functionals defined on every normed vector space to make the study of the dual space "interesting". Another version of the Hahn–Banach theorem is known as the Hahn–Banach separation theorem or the hyperplane separation theorem, and has numerous uses in convex geometry.
In topology, the Tietze extension theorem states that continuous functions on a closed subset of a normal topological space can be extended to the entire space, preserving boundedness if necessary.
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces. They are sometimes called Lebesgue spaces, named after Henri Lebesgue, although according to the Bourbaki group they were first introduced by Frigyes Riesz. Lp spaces form an important class of Banach spaces in functional analysis, and of topological vector spaces. Because of their key role in the mathematical analysis of measure and probability spaces, Lebesgue spaces are used also in the theoretical discussion of problems in physics, statistics, economics, finance, engineering, and other disciplines.
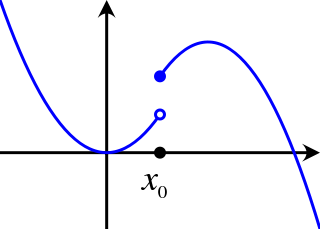
In mathematical analysis, semicontinuity is a property of extended real-valued functions that is weaker than continuity. An extended real-valued function is uppersemicontinuous at a point if, roughly speaking, the function values for arguments near are not much higher than
In the area of mathematics known as functional analysis, a reflexive space is a locally convex topological vector space (TVS) for which the canonical evaluation map from into its bidual is an isomorphism of TVSs. Since a normable TVS is reflexive if and only if it is semi-reflexive, every normed space is reflexive if and only if the canonical evaluation map from into its bidual is surjective; in this case the normed space is necessarily also a Banach space. In 1951, R. C. James discovered a Banach space, now known as James' space, that is not reflexive but is nevertheless isometrically isomorphic to its bidual.
In functional analysis and related areas of mathematics, Fréchet spaces, named after Maurice Fréchet, are special topological vector spaces. They are generalizations of Banach spaces. All Banach and Hilbert spaces are Fréchet spaces. Spaces of infinitely differentiable functions are typical examples of Fréchet spaces, many of which are typically not Banach spaces.
In mathematics, the uniform boundedness principle or Banach–Steinhaus theorem is one of the fundamental results in functional analysis. Together with the Hahn–Banach theorem and the open mapping theorem, it is considered one of the cornerstones of the field. In its basic form, it asserts that for a family of continuous linear operators whose domain is a Banach space, pointwise boundedness is equivalent to uniform boundedness in operator norm.
The Arzelà–Ascoli theorem is a fundamental result of mathematical analysis giving necessary and sufficient conditions to decide whether every sequence of a given family of real-valued continuous functions defined on a closed and bounded interval has a uniformly convergent subsequence. The main condition is the equicontinuity of the family of functions. The theorem is the basis of many proofs in mathematics, including that of the Peano existence theorem in the theory of ordinary differential equations, Montel's theorem in complex analysis, and the Peter–Weyl theorem in harmonic analysis and various results concerning compactness of integral operators.
In the mathematical area of game theory, a minimax theorem is a theorem providing conditions that guarantee that the max–min inequality is also an equality. The first theorem in this sense is von Neumann's minimax theorem from 1928, which was considered the starting point of game theory. Since then, several generalizations and alternative versions of von Neumann's original theorem have appeared in the literature.
In mathematics and mathematical optimization, the convex conjugate of a function is a generalization of the Legendre transformation which applies to non-convex functions. It is also known as Legendre–Fenchel transformation, Fenchel transformation, or Fenchel conjugate. It allows in particular for a far reaching generalization of Lagrangian duality.
In functional analysis and related areas of mathematics, a barrelled space is a topological vector space (TVS) for which every barrelled set in the space is a neighbourhood for the zero vector. A barrelled set or a barrel in a topological vector space is a set that is convex, balanced, absorbing, and closed. Barrelled spaces are studied because a form of the Banach–Steinhaus theorem still holds for them. Barrelled spaces were introduced by Bourbaki (1950).
In functional and convex analysis, and related disciplines of mathematics, the polar set is a special convex set associated to any subset of a vector space lying in the dual space The bipolar of a subset is the polar of but lies in .
In mathematics, particularly in functional analysis, a bornological space is a type of space which, in some sense, possesses the minimum amount of structure needed to address questions of boundedness of sets and linear maps, in the same way that a topological space possesses the minimum amount of structure needed to address questions of continuity. Bornological spaces are distinguished by the property that a linear map from a bornological space into any locally convex spaces is continuous if and only if it is a bounded linear operator.
In linear algebra, a cone—sometimes called a linear cone for distinguishing it from other sorts of cones—is a subset of a vector space that is closed under scalar multiplication; that is, C is a cone if implies for every scalar s.
In mathematics, a quasiconvex function is a real-valued function defined on an interval or on a convex subset of a real vector space such that the inverse image of any set of the form is a convex set. For a function of a single variable, along any stretch of the curve the highest point is one of the endpoints. The negative of a quasiconvex function is said to be quasiconcave.
In the mathematical theory of games, in particular the study of zero-sum continuous games, not every game has a minimax value. This is the expected value to one of the players when both play a perfect strategy.
In functional analysis, a branch of mathematics, a selection theorem is a theorem that guarantees the existence of a single-valued selection function from a given set-valued map. There are various selection theorems, and they are important in the theories of differential inclusions, optimal control, and mathematical economics.
In functional analysis and related areas of mathematics, the strong dual space of a topological vector space (TVS) is the continuous dual space of equipped with the strong (dual) topology or the topology of uniform convergence on bounded subsets of where this topology is denoted by or The coarsest polar topology is called weak topology. The strong dual space plays such an important role in modern functional analysis, that the continuous dual space is usually assumed to have the strong dual topology unless indicated otherwise. To emphasize that the continuous dual space, has the strong dual topology, or may be written.
This is a glossary for the terminology in a mathematical field of functional analysis.
 | This mathematical analysis–related article is a stub. You can help Wikipedia by expanding it. |
 | This game theory article is a stub. You can help Wikipedia by expanding it. |
