Slam-dunk

Last updated February 22, 2019

In the mathematical field of low-dimensional topology, the slam-dunk is a particular modification of a given surgery diagram in the 3-sphere for a 3-manifold. The name, but not the move, is due to Tim Cochran. Let K be a component of the link in the diagram and J be a component that circles K as a meridian. Suppose K has integer coefficient n and J has coefficient a rational number r. Then we can obtain a new diagram by deleting J and changing the coefficient of K to n-1/r. This is the slam-dunk.

Mathematics includes the study of such topics as quantity, structure, space, and change.

In mathematics, low-dimensional topology is the branch of topology that studies manifolds, or more generally topological spaces, of four or fewer dimensions. Representative topics are the structure theory of 3-manifolds and 4-manifolds, knot theory, and braid groups. It can be regarded as a part of geometric topology. It may also be used to refer to the study of topological spaces of dimension 1, though this is more typically considered part of continuum theory.

In topology, a branch of mathematics, a Dehn surgery, named after Max Dehn, is a construction used to modify 3-manifolds. The process takes as input a 3-manifold together with a link. It is often conceptualized as two steps: drilling then filling.

The name of the move is suggested by the proof that these diagrams give the same 3-manifold. First, do the surgery on K, replacing a tubular neighborhood of K by another solid torus T according to the surgery coefficient n. Since J is a meridian, it can be pushed, or "slam dunked", into T. Since n is an integer, J intersects the meridian of T once, and so J must be isotopic to a longitude of T. Thus when we now do surgery on J, we can think of it as replacing T by another solid torus. This replacement, as shown by a simple calculation, is given by coefficient n - 1/r.

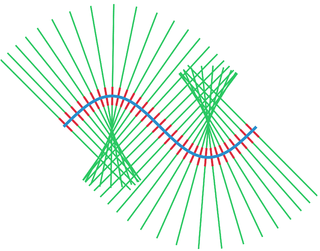
In mathematics, a tubular neighborhood of a submanifold of a smooth manifold is an open set around it resembling the normal bundle.

In mathematics, a solid torus is the topological space formed by sweeping a disk around a circle. It is homeomorphic to the Cartesian product $of the disk and the circle, endowed with the product topology. A standard way to visualize a solid torus is as a toroid, embedded in 3-space. However, it should be distinguished from a torus, which has the same visual appearance: the torus is the two-dimensional space on the boundary of a toroid, while the solid torus includes also the compact interior space enclosed by the torus.$

A slam dunk, also simply dunk, is a type of basketball shot that is performed when a player jumps in the air, controls the ball above the horizontal plane of the rim, and scores by putting the ball directly through the basket with one or both hands. It is considered a type of field goal; if successful, it is worth two points. Such a shot was known as a "dunk shot" until the term "slam dunk" was coined by former Los Angeles Lakers announcer Chick Hearn.

The inverse of the slam-dunk can be used to change any rational surgery diagram into an integer one, i.e. a surgery diagram on a framed link.

Related Research Articles

Elliptic curve an algebraic curve of genus 1 equipped with a basepoint

In mathematics, an elliptic curve is a plane algebraic curve defined by an equation of the form

In mathematics, genus has a few different, but closely related, meanings. The most common concept, the genus of an (orientable) surface, is the number of "holes" it has. This is made more precise below.

In mathematics, homology is a general way of associating a sequence of algebraic objects such as abelian groups or modules to other mathematical objects such as topological spaces. Homology groups were originally defined in algebraic topology. Similar constructions are available in a wide variety of other contexts, such as abstract algebra, groups, Lie algebras, Galois theory, and algebraic geometry.

In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life, such as those in shoelaces and rope, a mathematical knot differs in that the ends are joined together so that it cannot be undone, the simplest knot being a ring. In mathematical language, a knot is an embedding of a circle in 3-dimensional Euclidean space, R³. Two mathematical knots are equivalent if one can be transformed into the other via a deformation of R³ upon itself ; these transformations correspond to manipulations of a knotted string that do not involve cutting the string or passing the string through itself.

Weyl group Subgroup of a root systems isometry group

In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection group. Abstractly, Weyl groups are finite Coxeter groups, and are important examples of these.

In algebraic topology, the Betti numbers are used to distinguish topological spaces based on the connectivity of n-dimensional simplicial complexes. For the most reasonable finite-dimensional spaces, the sequence of Betti numbers is 0 from some point onward, and they are all finite.

In mathematics, a knot is an embedding of a circle $S 1$ in 3-dimensional Euclidean space, $R 3$ , considered up to continuous deformations (isotopies). A crucial difference between the standard mathematical and conventional notions of a knot is that mathematical knots are closed—there are no ends to tie or untie on a mathematical knot. Physical properties such as friction and thickness also do not apply, although there are mathematical definitions of a knot that take such properties into account. The term knot is also applied to embeddings of $S j$ in $S n$ , especially in the case $j = n - 2$ . The branch of mathematics that studies knots is known as knot theory, and has many simple relations to graph theory.

In mathematics, the linking number is a numerical invariant that describes the linking of two closed curves in three-dimensional space. Intuitively, the linking number represents the number of times that each curve winds around the other. The linking number is always an integer, but may be positive or negative depending on the orientation of the two curves.

In mathematics, Kronecker's theorem is a theorem about diophantine approximation, introduced by Leopold Kronecker (1884).

In geometric topology, a field within mathematics, the obstruction to a homotopy equivalence $of finite CW-complexes being a simple homotopy equivalence is its Whitehead torsion which is an element in the Whitehead group . These concepts are named after the mathematician J. H. C. Whitehead.$

In mathematics, the Kirby calculus in geometric topology, named after Robion Kirby, is a method for modifying framed links in the 3-sphere using a finite set of moves, the Kirby moves. Using four-dimensional Cerf theory, he proved that if M and N are 3-manifolds, resulting from Dehn surgery on framed links L and J respectively, then they are homeomorphic if and only if L and J are related by a sequence of Kirby moves. According to the Lickorish–Wallace theorem any closed orientable 3-manifold is obtained by such surgery on some link in the 3-sphere.

In the mathematical field of knot theory, the Jones polynomial is a knot polynomial discovered by Vaughan Jones in 1984.,. Specifically, it is an invariant of an oriented knot or link which assigns to each oriented knot or link a Laurent polynomial in the variable $with integer coefficients.$

In mathematics, the Alexander polynomial is a knot invariant which assigns a polynomial with integer coefficients to each knot type. James Waddell Alexander II discovered this, the first knot polynomial, in 1923. In 1969, John Conway showed a version of this polynomial, now called the Alexander–Conway polynomial, could be computed using a skein relation, although its significance was not realized until the discovery of the Jones polynomial in 1984. Soon after Conway's reworking of the Alexander polynomial, it was realized that a similar skein relation was exhibited in Alexander's paper on his polynomial.

In mathematics, the Whitehead manifold is an open 3-manifold that is contractible, but not homeomorphic to $. J. H. C. Whitehead (1935) discovered this puzzling object while he was trying to prove the Poincaré conjecture, correcting an error in an earlier paper Whitehead where he incorrectly claimed that no such manifold exists.$

In mathematics and computer algebra, factorization of polynomials or polynomial factorization is the process of expressing a polynomial with coefficients in a given field or in the integers as the product of irreducible factors with coefficients in the same domain. Polynomial factorization is one of the fundamental tools of the computer algebra systems.

In mathematics, hyperbolic Dehn surgery is an operation by which one can obtain further hyperbolic 3-manifolds from a given cusped hyperbolic 3-manifold. Hyperbolic Dehn surgery exists only in dimension three and is one which distinguishes hyperbolic geometry in three dimensions from other dimensions.

In mathematics, especially in the area of mathematical analysis known as dynamical systems theory, a linear flow on the torus is a flow on the n-dimensional torus

In the mathematical field of low-dimensional topology, a clasper is a surface in a 3-manifold on which surgery can be performed.

References

Robert Gompf and Andras Stipsicz, 4-Manifolds and Kirby Calculus, (1999) (Volume 20 in Graduate Studies in Mathematics ), American Mathematical Society, Providence, RI ISBN 0-8218-0994-6

Robert Ernest Gompf is an American mathematician specializing in geometric topology.

Graduate Studies in Mathematics (GSM) is a series of graduate-level textbooks in mathematics published by the American Mathematical Society (AMS). These books elaborate on several theories from notable personas, such as Martin Schechter and Terence Tao, in the mathematical industry. The books in this series are published only in hardcover.

International Standard Book Number Unique numeric book identifier

The International Standard Book Number (ISBN) is a numeric commercial book identifier which is intended to be unique. Publishers purchase ISBNs from an affiliate of the International ISBN Agency.

This topology-related article is a stub. You can help Wikipedia by expanding it.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.