In mathematics, the inverse limit is a construction that allows one to "glue together" several related objects, the precise gluing process being specified by morphisms between the objects. Thus, inverse limits can be defined in any category although their existence depends on the category that is considered. They are a special case of the concept of limit in category theory.
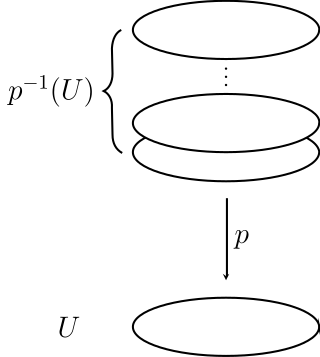
In topology, a covering or covering projection is a map between topological spaces that, intuitively, locally acts like a projection of multiple copies of a space onto itself. In particular, coverings are special types of local homeomorphisms. If is a covering, is said to be a covering space or cover of , and is said to be the base of the covering, or simply the base. By abuse of terminology, and may sometimes be called covering spaces as well. Since coverings are local homeomorphisms, a covering space is a special kind of étalé space.

In mathematics, the inverse trigonometric functions are the inverse functions of the trigonometric functions, under suitably restricted domains. Specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, and are used to obtain an angle from any of the angle's trigonometric ratios. Inverse trigonometric functions are widely used in engineering, navigation, physics, and geometry.
The Basel problem is a problem in mathematical analysis with relevance to number theory, concerning an infinite sum of inverse squares. It was first posed by Pietro Mengoli in 1650 and solved by Leonhard Euler in 1734, and read on 5 December 1735 in The Saint Petersburg Academy of Sciences. Since the problem had withstood the attacks of the leading mathematicians of the day, Euler's solution brought him immediate fame when he was twenty-eight. Euler generalised the problem considerably, and his ideas were taken up more than a century later by Bernhard Riemann in his seminal 1859 paper "On the Number of Primes Less Than a Given Magnitude", in which he defined his zeta function and proved its basic properties. The problem is named after the city of Basel, hometown of Euler as well as of the Bernoulli family who unsuccessfully attacked the problem.
In mathematics, the Riemann–Lebesgue lemma, named after Bernhard Riemann and Henri Lebesgue, states that the Fourier transform or Laplace transform of an L1 function vanishes at infinity. It is of importance in harmonic analysis and asymptotic analysis.

In geometry, a three-dimensional space is a mathematical space in which three values (coordinates) are required to determine the position of a point. Most commonly, it is the three-dimensional Euclidean space, that is, the Euclidean space of dimension three, which models physical space. More general three-dimensional spaces are called 3-manifolds. The term may also refer colloquially to a subset of space, a three-dimensional region, a solid figure.
In mathematics, Fejér's theorem, named after Hungarian mathematician Lipót Fejér, states the following:
In the fields of actuarial science and financial economics there are a number of ways that risk can be defined; to clarify the concept theoreticians have described a number of properties that a risk measure might or might not have. A coherent risk measure is a function that satisfies properties of monotonicity, sub-additivity, homogeneity, and translational invariance.
In mathematics, the Wasserstein distance or Kantorovich–Rubinstein metric is a distance function defined between probability distributions on a given metric space . It is named after Leonid Vaseršteĭn.

In mathematics, a sequence of nested intervals can be intuitively understood as an ordered collection of intervals on the real number line with natural numbers as an index. In order for a sequence of intervals to be considered nested intervals, two conditions have to be met:
- Every interval in the sequence is contained in the previous one.
- The length of the intervals get arbitrarily small.

In mathematics, an ordered vector space or partially ordered vector space is a vector space equipped with a partial order that is compatible with the vector space operations.
In mathematics, the Loomis–Whitney inequality is a result in geometry, which in its simplest form, allows one to estimate the "size" of a -dimensional set by the sizes of its -dimensional projections. The inequality has applications in incidence geometry, the study of so-called "lattice animals", and other areas.
In mathematics, Kan complexes and Kan fibrations are part of the theory of simplicial sets. Kan fibrations are the fibrations of the standard model category structure on simplicial sets and are therefore of fundamental importance. Kan complexes are the fibrant objects in this model category. The name is in honor of Daniel Kan.
In financial mathematics, a risk measure is used to determine the amount of an asset or set of assets to be kept in reserve. The purpose of this reserve is to make the risks taken by financial institutions, such as banks and insurance companies, acceptable to the regulator. In recent years attention has turned to convex and coherent risk measurement.
The Brownian motion models for financial markets are based on the work of Robert C. Merton and Paul A. Samuelson, as extensions to the one-period market models of Harold Markowitz and William F. Sharpe, and are concerned with defining the concepts of financial assets and markets, portfolios, gains and wealth in terms of continuous-time stochastic processes.
In financial mathematics, acceptance set is a set of acceptable future net worth which is acceptable to the regulator. It is related to risk measures.
The bid–ask matrix is a matrix with elements corresponding with exchange rates between the assets. These rates are in physical units and not with respect to any numeraire. The element of the matrix is the number of units of asset which can be exchanged for 1 unit of asset .
Stochastic portfolio theory (SPT) is a mathematical theory for analyzing stock market structure and portfolio behavior introduced by E. Robert Fernholz in 2002. It is descriptive as opposed to normative, and is consistent with the observed behavior of actual markets. Normative assumptions, which serve as a basis for earlier theories like modern portfolio theory (MPT) and the capital asset pricing model (CAPM), are absent from SPT.
In differential geometry, the integration along fibers of a k-form yields a -form where m is the dimension of the fiber, via "integration". It is also called the fiber integration.
In the branch of mathematics known as integration theory, the McShane integral, created by Edward J. McShane, is a modification of the Henstock-Kurzweil integral. The McShane integral is equivalent to the Lebesgue integral.


























