Somos sequence

Last updated February 06, 2025

In mathematics, a Somos sequence is a sequence of numbers defined by a certain recurrence relation, described below. They were discovered by mathematician Michael Somos. From the form of their defining recurrence (which involves division), one would expect the terms of the sequence to be fractions, but surprisingly, a few Somos sequences have the property that all of their members are integers.

Recurrence equations

For an integer number k larger than 1, the Somos-k sequence $(a_{0},a_{1},a_{2},\ldots )$ is defined by the equation

a_{n}a_{n-k}=a_{n-1}a_{n-k+1}+a_{n-2}a_{n-k+2}+\cdots +a_{n-(k-1)/2}a_{n-(k+1)/2}

when k is odd, or by the analogous equation

a_{n}a_{n-k}=a_{n-1}a_{n-k+1}+a_{n-2}a_{n-k+2}+\cdots +(a_{n-k/2})^{2}

when k is even, together with the initial values

a_i = 1 for i < k.

For k = 2 or 3, these recursions are very simple (there is no addition on the right-hand side) and they define the all-ones sequence (1, 1, 1, 1, 1, 1, ...). In the first nontrivial case, k = 4, the defining equation is

a_{n}a_{n-4}=a_{n-1}a_{n-3}+a_{n-2}^{2}

while for k = 5 the equation is

a_{n}a_{n-5}=a_{n-1}a_{n-4}+a_{n-2}a_{n-3}\,.

These equations can be rearranged into the form of a recurrence relation, in which the value a_n on the left hand side of the recurrence is defined by a formula on the right hand side, by dividing the formula by a_n − k. For k = 4, this yields the recurrence

a_{n}={\frac {a_{n-1}a_{n-3}+a_{n-2}^{2}}{a_{n-4}}}

while for k = 5 it gives the recurrence

a_{n}={\frac {a_{n-1}a_{n-4}+a_{n-2}a_{n-3}}{a_{n-5}}}.

While in the usual definition of the Somos sequences, the values of a_i for i < k are all set equal to 1, it is also possible to define other sequences by using the same recurrences with different initial values.

Sequence values

The values in the Somos-4 sequence are

1, 1, 1, 1, 2, 3, 7, 23, 59, 314, 1529, 8209, 83313, 620297, 7869898, ... (sequence A006720 in the OEIS ).

The values in the Somos-5 sequence are

1, 1, 1, 1, 1, 2, 3, 5, 11, 37, 83, 274, 1217, 6161, 22833, 165713, ... (sequence A006721 in the OEIS ).

The values in the Somos-6 sequence are

1, 1, 1, 1, 1, 1, 3, 5, 9, 23, 75, 421, 1103, 5047, 41783, 281527, ... (sequence A006722 in the OEIS ).

The values in the Somos-7 sequence are

1, 1, 1, 1, 1, 1, 1, 3, 5, 9, 17, 41, 137, 769, 1925, 7203, 34081, ... (sequence A006723 in the OEIS ).

The first 17 values in the Somos-8 sequence are

1, 1, 1, 1, 1, 1, 1, 1, 4, 7, 13, 25, 61, 187, 775, 5827, 14815 [the next value is fractional].^[1]

Integrality

The form of the recurrences describing the Somos sequences involves divisions, making it appear likely that the sequences defined by these recurrence will contain fractional values. Nevertheless, for k ≤ 7 the Somos sequences contain only integer values.^[2]^[3]^[4] Several mathematicians have studied the problem of proving and explaining this integer property of the Somos sequences; it is closely related to the combinatorics of cluster algebras.^[5]^[3]^[6]^[7]

For k ≥ 8 the analogously defined sequences eventually contain fractional values. For Somos-8 the first fractional value is the 18th term with value 420514/7.

For k < 7, changing the initial values (but using the same recurrence relation) also typically results in fractional values.

Related Research Articles

In mathematics, the factorial of a non-negative integer $,$ denoted by $,$ is the product of all positive integers less than or equal to $.$ The factorial of also equals the product of $with the next smaller factorial: For example, The value of 0! is 1, according to the convention for an empty product.$

In mathematics, a recurrence relation is an equation according to which the $th term of a sequence of numbers is equal to some combination of the previous terms. Often, only previous terms of the sequence appear in the equation, for a parameter that is independent of; this number is called the order of the relation. If the values of the first numbers in the sequence have been given, the rest of the sequence can be calculated by repeatedly applying the equation.$

In combinatorial mathematics, the Bell numbers count the possible partitions of a set. These numbers have been studied by mathematicians since the 19th century, and their roots go back to medieval Japan. In an example of Stigler's law of eponymy, they are named after Eric Temple Bell, who wrote about them in the 1930s.

In mathematics, the Thue–Morse or Prouhet–Thue–Morse sequence is the binary sequence that can be obtained by starting with 0 and successively appending the Boolean complement of the sequence obtained thus far. It is sometimes called the fair share sequence because of its applications to fair division or parity sequence. The first few steps of this procedure yield the strings 0, 01, 0110, 01101001, 0110100110010110, and so on, which are the prefixes of the Thue–Morse sequence. The full sequence begins:

In mathematics, the double factorial of a number $n$ , denoted by $n ‼$ , is the product of all the positive integers up to $n$ that have the same parity as $n$ . That is,

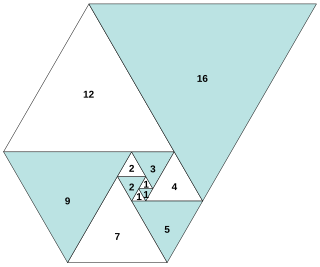
In number theory, the Padovan sequence is the sequence of integers P(n) defined by the initial values

In mathematical analysis and number theory, Somos' quadratic recurrence constant or simply Somos' constant is a constant defined as an expression of infinitely many nested square roots. It arises when studying the asymptotic behaviour of a certain sequence and also in connection to the binary representations of real numbers between zero and one. The constant named after Michael Somos. It is defined by:

<span class="mw-page-title-main">Sylvester's sequence</span> Doubly exponential integer sequence

In number theory, Sylvester's sequence is an integer sequence in which each term is the product of the previous terms, plus one. Its first few terms are

<span class="mw-page-title-main">Ordered Bell number</span> Number of weak orderings

In number theory and enumerative combinatorics, the ordered Bell numbers or Fubini numbers count the weak orderings on a set of $elements. Weak orderings arrange their elements into a sequence allowing ties, such as might arise as the outcome of a horse race.$

In mathematics, the Jacobsthal numbers are an integer sequence named after the German mathematician Ernst Jacobsthal. Like the related Fibonacci numbers, they are a specific type of Lucas sequence $for which P = 1, and Q = -2—and are defined by a similar recurrence relation: in simple terms, the sequence starts with 0 and 1, then each following number is found by adding the number before it to twice the number before that. The first Jacobsthal numbers are:$

In combinatorial mathematics, a partial permutation, or sequence without repetition, on a finite set S is a bijection between two specified subsets of S. That is, it is defined by two subsets U and V of equal size, and a one-to-one mapping from U to V. Equivalently, it is a partial function on S that can be extended to a permutation.

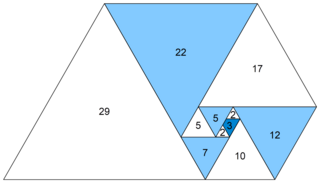
In mathematics, the Perrin numbers are a doubly infinite constant-recursive integer sequence with characteristic equation $x 3 = x + 1$ . The Perrin numbers bear the same relationship to the Padovan sequence as the Lucas numbers do to the Fibonacci sequence.

In combinatorics, the Schröder–Hipparchus numbers form an integer sequence that can be used to count the plane trees with a given set of leaves, the ways of inserting parentheses into a sequence, and the ways of dissecting a convex polygon into smaller polygons by inserting diagonals. These numbers begin

In mathematics, the telephone numbers or the involution numbers form a sequence of integers that count the ways $n$ people can be connected by person-to-person telephone calls. These numbers also describe the number of matchings of a complete graph on $n$ vertices, the number of permutations on $n$ elements that are involutions, the sum of absolute values of coefficients of the Hermite polynomials, the number of standard Young tableaux with $n$ cells, and the sum of the degrees of the irreducible representations of the symmetric group. Involution numbers were first studied in 1800 by Heinrich August Rothe, who gave a recurrence equation by which they may be calculated, giving the values

In combinatorial mathematics and statistics, the Fuss–Catalan numbers are numbers of the form

The metallic mean of a natural number $n$ is a positive real number, denoted here $that satisfies the following equivalent characterizations:$

<span class="mw-page-title-main">Constant-recursive sequence</span> Infinite sequence of numbers satisfying a linear equation

In mathematics, an infinite sequence of numbers $is called constant-recursive if it satisfies an equation of the form$

In mathematics, a Göbel sequence is a sequence of rational numbers defined by the recurrence relation

In mathematics, a Stanley sequence is an integer sequence generated by a greedy algorithm that chooses the sequence members to avoid arithmetic progressions. If $is a finite set of non-negative integers on which no three elements form an arithmetic progression, then the Stanley sequence generated from starts from the elements of, in sorted order, and then repeatedly chooses each successive element of the sequence to be a number that is larger than the already-chosen numbers and does not form any three-term arithmetic progression with them. These sequences are named after Richard P. Stanley.$

Narayana polynomials are a class of polynomials whose coefficients are the Narayana numbers. The Narayana numbers and Narayana polynomials are named after the Canadian mathematician T. V. Narayana (1930–1987). They appear in several combinatorial problems.

References

↑ Mase, Takafumi (2013), "The Laurent phenomenon and discrete integrable systems" (PDF), The breadth and depth of nonlinear discrete integrable systems, RIMS Kôkyûroku Bessatsu, vol. B41, Res. Inst. Math. Sci. (RIMS), Kyoto, pp. 43–64, MR 3220414
↑ Malouf, Janice L. (1992), "An integer sequence from a rational recursion", Discrete Mathematics , 110 (1–3): 257–261, doi: 10.1016/0012-365X(92)90714-Q .
1 2 Carroll, Gabriel D.; Speyer, David E. (2004), "The Cube Recurrence", Electronic Journal of Combinatorics , 11: R73, arXiv: math.CO/0403417 , doi:10.37236/1826, S2CID 1446749 .
↑ "A Bare-Bones Chronology of Somos Sequences", faculty.uml.edu, retrieved 2023-11-27
↑ Fomin, Sergey; Zelevinsky, Andrei (2002), "The Laurent phenomenon", Advances in Applied Mathematics , 28 (2): 119–144, arXiv: math.CO/0104241 , doi:10.1006/aama.2001.0770, S2CID 119157629 .
↑ Hone, Andrew N. W. (2023), "Casting light on shadow Somos sequences", Glasgow Mathematical Journal, 65 (S1): S87 –S101, arXiv: 2111.10905 , doi:10.1017/S0017089522000167, MR 4594276
↑ Stone, Alex (18 November 2023), "The Astonishing Behavior of Recursive Sequences", Quanta Magazine

External links

Jim Propp's Somos Sequence Site
Weisstein, Eric W., "Somos Sequence", MathWorld
The Troublemaker Number. Numberphile video on the Somos sequences

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Mase, Takafumi (2013), "The Laurent phenomenon and discrete integrable systems" (PDF), The breadth and depth of nonlinear discrete integrable systems, RIMS Kôkyûroku Bessatsu, vol. B41, Res. Inst. Math. Sci. (RIMS), Kyoto, pp. 43–64, MR 3220414

[2] Malouf, Janice L. (1992), "An integer sequence from a rational recursion", Discrete Mathematics , 110 (1–3): 257–261, doi: 10.1016/0012-365X(92)90714-Q .

[:0-3] 1 2 Carroll, Gabriel D.; Speyer, David E. (2004), "The Cube Recurrence", Electronic Journal of Combinatorics , 11: R73, arXiv: math.CO/0403417 , doi:10.37236/1826, S2CID 1446749 .

[4] "A Bare-Bones Chronology of Somos Sequences", faculty.uml.edu, retrieved 2023-11-27

[5] Fomin, Sergey; Zelevinsky, Andrei (2002), "The Laurent phenomenon", Advances in Applied Mathematics , 28 (2): 119–144, arXiv: math.CO/0104241 , doi:10.1006/aama.2001.0770, S2CID 119157629 .

[6] Hone, Andrew N. W. (2023), "Casting light on shadow Somos sequences", Glasgow Mathematical Journal, 65 (S1): S87 –S101, arXiv: 2111.10905 , doi:10.1017/S0017089522000167, MR 4594276

[7] Stone, Alex (18 November 2023), "The Astonishing Behavior of Recursive Sequences", Quanta Magazine

[1]

[2]

[3]

[4]

[5]

[6]

[7]