A Sparse graph code is a code which is represented by a sparse graph.
Any linear code can be represented as a graph, where there are two sets of nodes - a set representing the transmitted bits and another set representing the constraints that the transmitted bits have to satisfy. The state of the art classical error-correcting codes are based on sparse graphs, achieving close to the Shannon limit. The archetypal sparse-graph codes are Gallager's low-density parity-check codes.
 | This article about matrices is a stub. You can help Wikipedia by expanding it. |
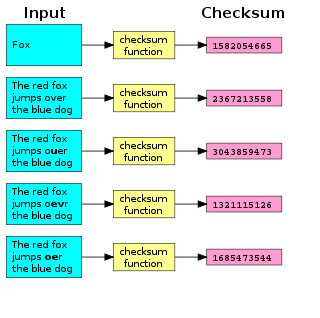
A checksum is a small-sized block of data derived from another block of digital data for the purpose of detecting errors that may have been introduced during its transmission or storage. By themselves, checksums are often used to verify data integrity but are not relied upon to verify data authenticity.
In information theory and coding theory with applications in computer science and telecommunication, error detection and correction (EDAC) or error control are techniques that enable reliable delivery of digital data over unreliable communication channels. Many communication channels are subject to channel noise, and thus errors may be introduced during transmission from the source to a receiver. Error detection techniques allow detecting such errors, while error correction enables reconstruction of the original data in many cases.
A cyclic redundancy check (CRC) is an error-detecting code commonly used in digital networks and storage devices to detect accidental changes to digital data. Blocks of data entering these systems get a short check value attached, based on the remainder of a polynomial division of their contents. On retrieval, the calculation is repeated and, in the event the check values do not match, corrective action can be taken against data corruption. CRCs can be used for error correction.
In digital transmission, the number of bit errors is the numbers of received bits of a data stream over a communication channel that have been altered due to noise, interference, distortion or bit synchronization errors.
In computer science and telecommunication, Hamming codes are a family of linear error-correcting codes. Hamming codes can detect one-bit and two-bit errors, or correct one-bit errors without detection of uncorrected errors. By contrast, the simple parity code cannot correct errors, and can detect only an odd number of bits in error. Hamming codes are perfect codes, that is, they achieve the highest possible rate for codes with their block length and minimum distance of three. Richard W. Hamming invented Hamming codes in 1950 as a way of automatically correcting errors introduced by punched card readers. In his original paper, Hamming elaborated his general idea, but specifically focused on the Hamming(7,4) code which adds three parity bits to four bits of data.
The Universal Product Code is a barcode symbology that is widely used worldwide for tracking trade items in stores.
A universal asynchronous receiver-transmitter is a computer hardware device for asynchronous serial communication in which the data format and transmission speeds are configurable. It sends data bits one by one, from the least significant to the most significant, framed by start and stop bits so that precise timing is handled by the communication channel. The electric signaling levels are handled by a driver circuit external to the UART. Common signal levels are RS-232, RS-485, and raw TTL for short debugging links. Early teletypewriters used current loops.
On computers, a serial port is a serial communication interface through which information transfers in or out sequentially one bit at a time. This is in contrast to a parallel port, which communicates multiple bits simultaneously in parallel. Throughout most of the history of personal computers, data has been transferred through serial ports to devices such as modems, terminals, various peripherals, and directly between computers.
A parity bit, or check bit, is a bit added to a string of binary code. Parity bits are a simple form of error detecting code. Parity bits are generally applied to the smallest units of a communication protocol, typically 8-bit octets (bytes), although they can also be applied separately to an entire message string of bits.
WWVB is a time signal radio station near Fort Collins, Colorado and is operated by the National Institute of Standards and Technology (NIST). Most radio-controlled clocks in North America use WWVB's transmissions to set the correct time. The 70 kW ERP signal transmitted from WWVB is a continuous 60 kHz carrier wave, the frequency of which is derived from a set of atomic clocks located at the transmitter site, yielding a frequency uncertainty of less than 1 part in 1012. A one-bit-per-second time code, which is based on the IRIG "H" time code format and derived from the same set of atomic clocks, is then modulated onto the carrier wave using pulse-width modulation and amplitude-shift keying. A single complete frame of time code begins at the start of each minute, lasts one minute, and conveys the year, day of year, hour, minute, and other information as of the beginning of the minute.
In information theory, a low-density parity-check (LDPC) code is a linear error correcting code, a method of transmitting a message over a noisy transmission channel. An LDPC code is constructed using a sparse Tanner graph. LDPC codes are capacity-approaching codes, which means that practical constructions exist that allow the noise threshold to be set very close to the theoretical maximum for a symmetric memoryless channel. The noise threshold defines an upper bound for the channel noise, up to which the probability of lost information can be made as small as desired. Using iterative belief propagation techniques, LDPC codes can be decoded in time linear to their block length.
In coding theory, a linear code is an error-correcting code for which any linear combination of codewords is also a codeword. Linear codes are traditionally partitioned into block codes and convolutional codes, although turbo codes can be seen as a hybrid of these two types. Linear codes allow for more efficient encoding and decoding algorithms than other codes.
Hybrid automatic repeat request is a combination of high-rate forward error correction (FEC) and automatic repeat request (ARQ) error-control. In standard ARQ, redundant bits are added to data to be transmitted using an error-detecting (ED) code such as a cyclic redundancy check (CRC). Receivers detecting a corrupted message will request a new message from the sender. In Hybrid ARQ, the original data is encoded with an FEC code, and the parity bits are either immediately sent along with the message or only transmitted upon request when a receiver detects an erroneous message. The ED code may be omitted when a code is used that can perform both forward error correction (FEC) in addition to error detection, such as a Reed–Solomon code. The FEC code is chosen to correct an expected subset of all errors that may occur, while the ARQ method is used as a fall-back to correct errors that are uncorrectable using only the redundancy sent in the initial transmission. As a result, hybrid ARQ performs better than ordinary ARQ in poor signal conditions, but in its simplest form this comes at the expense of significantly lower throughput in good signal conditions. There is typically a signal quality cross-over point below which simple hybrid ARQ is better, and above which basic ARQ is better.
In computing, telecommunication, information theory, and coding theory, forward error correction (FEC) or channel coding is a technique used for controlling errors in data transmission over unreliable or noisy communication channels.
Error correction code memory is a type of computer data storage that uses an error correction code (ECC) to detect and correct n-bit data corruption which occurs in memory. ECC memory is used in most computers where data corruption cannot be tolerated, like industrial control applications, critical databases, and infrastructural memory caches.
Remote error indication (REI) or formerly far end block error (FEBE) is an alarm signal used in synchronous optical networking (SONET). It indicates to the transmitting node that the receiver has detected a block error.
In computer science, repeat-accumulate codes are a low complexity class of error-correcting codes. They were devised so that their ensemble weight distributions are easy to derive. RA codes were introduced by Divsalar et al.
In coding theory, Hamming(7,4) is a linear error-correcting code that encodes four bits of data into seven bits by adding three parity bits. It is a member of a larger family of Hamming codes, but the term Hamming code often refers to this specific code that Richard W. Hamming introduced in 1950. At the time, Hamming worked at Bell Telephone Laboratories and was frustrated with the error-prone punched card reader, which is why he started working on error-correcting codes.
A multidimensional parity-check code (MDPC) is a simple type of error correcting code that operates by arranging the message into a multidimensional grid, and calculating a parity digit for each row and column. In general, an n-dimensional parity scheme can correct n/2 errors.
Sudoku codes are non-linear forward error correcting codes following rules of sudoku puzzles designed for an erasure channel. Based on this model, the transmitter sends a sequence of all symbols of a solved sudoku. The receiver either receives a symbol correctly or an erasure symbol to indicate that the symbol was not received. The decoder gets a matrix with missing entries and uses the constraints of sudoku puzzles to reconstruct a limited amount of erased symbols.