
A sphere is a geometrical object that is a three-dimensional analogue to a two-dimensional circle. Formally, a sphere is the set of points that are all at the same distance r from a given point in three-dimensional space. That given point is the center of the sphere, and r is the sphere's radius. The earliest known mentions of spheres appear in the work of the ancient Greek mathematicians.

In geometry, a geodesic is a curve representing in some sense the shortest path (arc) between two points in a surface, or more generally in a Riemannian manifold. The term also has meaning in any differentiable manifold with a connection. It is a generalization of the notion of a "straight line".

Packing problems are a class of optimization problems in mathematics that involve attempting to pack objects together into containers. The goal is to either pack a single container as densely as possible or pack all objects using as few containers as possible. Many of these problems can be related to real-life packaging, storage and transportation issues. Each packing problem has a dual covering problem, which asks how many of the same objects are required to completely cover every region of the container, where objects are allowed to overlap.
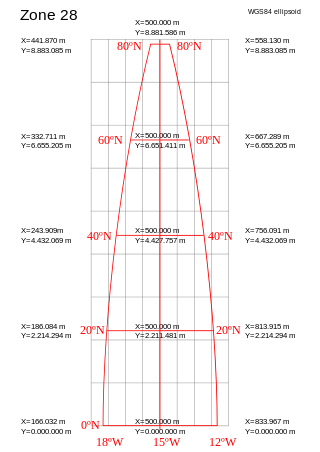
A projected coordinate system – also called a projected coordinate reference system, planar coordinate system, or grid reference system – is a type of spatial reference system that represents locations on Earth using Cartesian coordinates (x, y) on a planar surface created by a particular map projection. Each projected coordinate system, such as "Universal Transverse Mercator WGS 84 Zone 26N," is defined by a choice of map projection (with specific parameters), a choice of geodetic datum to bind the coordinate system to real locations on the earth, an origin point, and a choice of unit of measure. Hundreds of projected coordinate systems have been specified for various purposes in various regions.
In mathematics, the isoperimetric inequality is a geometric inequality involving the square of the circumference of a closed curve in the plane and the area of a plane region it encloses, as well as its various generalizations. Isoperimetric literally means "having the same perimeter". Specifically, the isoperimetric inequality states, for the length L of a closed curve and the area A of the planar region that it encloses, that

A Z-test is any statistical test for which the distribution of the test statistic under the null hypothesis can be approximated by a normal distribution. Z-test tests the mean of a distribution. For each significance level in the confidence interval, the Z-test has a single critical value which makes it more convenient than the Student's t-test whose critical values are defined by the sample size. Both the Z-test and Student's t-test have similarities in that they both help determine the significance of a set of data. However, the z-test is rarely used in practice because the population deviation is difficult to determine.

The great-circle distance, orthodromic distance, or spherical distance is the distance between two points on a sphere, measured along the great-circle arc between them. This arc is the shortest path between the two points on the surface of the sphere.
In geometry, the kissing number of a mathematical space is defined as the greatest number of non-overlapping unit spheres that can be arranged in that space such that they each touch a common unit sphere. For a given sphere packing in a given space, a kissing number can also be defined for each individual sphere as the number of spheres it touches. For a lattice packing the kissing number is the same for every sphere, but for an arbitrary sphere packing the kissing number may vary from one sphere to another.
The Hough transform is a feature extraction technique used in image analysis, computer vision, pattern recognition, and digital image processing. The purpose of the technique is to find imperfect instances of objects within a certain class of shapes by a voting procedure. This voting procedure is carried out in a parameter space, from which object candidates are obtained as local maxima in a so-called accumulator space that is explicitly constructed by the algorithm for computing the Hough transform.
In mathematics, and more specifically in geometry, parametrization is the process of finding parametric equations of a curve, a surface, or, more generally, a manifold or a variety, defined by an implicit equation. The inverse process is called implicitization. "To parameterize" by itself means "to express in terms of parameters".
In computer graphics, slerp is shorthand for spherical linear interpolation, introduced by Ken Shoemake in the context of quaternion interpolation for the purpose of animating 3D rotation. It refers to constant-speed motion along a unit-radius great circle arc, given the ends and an interpolation parameter between 0 and 1.
Random sample consensus (RANSAC) is an iterative method to estimate parameters of a mathematical model from a set of observed data that contains outliers, when outliers are to be accorded no influence on the values of the estimates. Therefore, it also can be interpreted as an outlier detection method. It is a non-deterministic algorithm in the sense that it produces a reasonable result only with a certain probability, with this probability increasing as more iterations are allowed. The algorithm was first published by Fischler and Bolles at SRI International in 1981. They used RANSAC to solve the location determination problem (LDP), where the goal is to determine the points in the space that project onto an image into a set of landmarks with known locations.

In astronomy, and in particular in astrodynamics, the osculating orbit of an object in space at a given moment in time is the gravitational Kepler orbit that it would have around its central body if perturbations were absent. That is, it is the orbit that coincides with the current orbital state vectors.
The n-vector representation is a three-parameter non-singular representation well-suited for replacing geodetic coordinates for horizontal position representation in mathematical calculations and computer algorithms.
A spherical design, part of combinatorial design theory in mathematics, is a finite set of N points on the d-dimensional unit d-sphereSd such that the average value of any polynomial f of degree t or less on the set equals the average value of f on the whole sphere. Such a set is often called a sphericalt-design to indicate the value of t, which is a fundamental parameter. The concept of a spherical design is due to Delsarte, Goethals, and Seidel, although these objects were understood as particular examples of cubature formulas earlier.
Light scattering by particles is the process by which small particles scatter light causing optical phenomena such as the blue color of the sky, and halos.

In geometry, the Tammes problem is a problem in packing a given number of points on the surface of a sphere such that the minimum distance between points is maximized. It is named after the Dutch botanist Pieter Merkus Lambertus Tammes who posed the problem in his 1930 doctoral dissertation on the distribution of pores on pollen grains.
The elliptic curve only hash (ECOH) algorithm was submitted as a candidate for SHA-3 in the NIST hash function competition. However, it was rejected in the beginning of the competition since a second pre-image attack was found.
Quantum optimization algorithms are quantum algorithms that are used to solve optimization problems. Mathematical optimization deals with finding the best solution to a problem from a set of possible solutions. Mostly, the optimization problem is formulated as a minimization problem, where one tries to minimize an error which depends on the solution: the optimal solution has the minimal error. Different optimization techniques are applied in various fields such as mechanics, economics and engineering, and as the complexity and amount of data involved rise, more efficient ways of solving optimization problems are needed. Quantum computing may allow problems which are not practically feasible on classical computers to be solved, or suggest a considerable speed up with respect to the best known classical algorithm.







