Spitzer's formula

Last updated August 27, 2021

In probability theory, Spitzer's formula or Spitzer's identity gives the joint distribution of partial sums and maximal partial sums of a collection of random variables. The result was first published by Frank Spitzer in 1956.^[1] The formula is regarded as "a stepping stone in the theory of sums of independent random variables".^[2]

Statement of theorem

Let $X_{1},X_{2},...$ be independent and identically distributed random variables and define the partial sums $S_{n}=X_{1},+X_{2}+...+X_{n}$ . Define $R_{n}={\text{max}}(0,S_{1},S_{2},...S_{n})$ . Then^[3]

\sum _{n=0}^{\infty }\phi _{n}(\alpha ,\beta )t^{n}=\exp \left[\sum _{n=1}^{\infty }{\frac {t^{n}}{n}}\left(u_{n}(\alpha )+v_{n}(\beta )-1\right)\right]

where

{\begin{aligned}\phi _{n}(\alpha ,\beta )&=\operatorname {E} (\exp \left[i(\alpha R_{n}+\beta (R_{n}-S_{n})\right])\\u_{n}(\alpha )&=\operatorname {E} (\exp \left[i\alpha S_{n}^{+}\right])\\v_{n}(\beta )&=\operatorname {E} (\exp \left[i\beta S_{n}^{-}\right])\end{aligned}}

and S^± denotes (|S| ± S)/2.

Proof

Two proofs are known, due to Spitzer^[1] and Wendel.^[3]

Related Research Articles

In probability theory and statistics, the exponential distribution is the probability distribution of the time between events in a Poisson point process, i.e., a process in which events occur continuously and independently at a constant average rate. It is a particular case of the gamma distribution. It is the continuous analogue of the geometric distribution, and it has the key property of being memoryless. In addition to being used for the analysis of Poisson point processes it is found in various other contexts.

Distributions, also known as Schwartz distributions or generalized functions, are objects that generalize the classical notion of functions in mathematical analysis. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative. Distributions are widely used in the theory of partial differential equations, where it may be easier to establish the existence of distributional solutions than classical solutions, or appropriate classical solutions may not exist. Distributions are also important in physics and engineering where many problems naturally lead to differential equations whose solutions or initial conditions are distributions, such as the Dirac delta function.

In mathematics, and specially in algebra, a formal series is an infinite sum that is considered independently from any notion of convergence, and can be manipulated with the usual algebraic operations on series.

In probability theory and statistics, the beta distribution is a family of continuous probability distributions defined on the interval [0, 1] parameterized by two positive shape parameters, denoted by α and β, that appear as exponents of the random variable and control the shape of the distribution. The generalization to multiple variables is called a Dirichlet distribution.

In probability theory and statistics, the gamma distribution is a two-parameter family of continuous probability distributions. The exponential distribution, Erlang distribution, and chi-square distribution are special cases of the gamma distribution. There are two different parameterizations in common use:

With a shape parameter k and a scale parameter θ.
With a shape parameter α = k and an inverse scale parameter β = 1/θ, called a rate parameter.

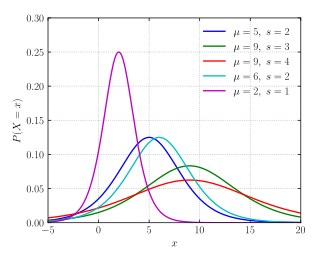
Logistic distribution continuous probability distribution

In probability theory and statistics, the logistic distribution is a continuous probability distribution. Its cumulative distribution function is the logistic function, which appears in logistic regression and feedforward neural networks. It resembles the normal distribution in shape but has heavier tails. The logistic distribution is a special case of the Tukey lambda distribution.

In probability theory, a compound Poisson distribution is the probability distribution of the sum of a number of independent identically-distributed random variables, where the number of terms to be added is itself a Poisson-distributed variable. In the simplest cases, the result can be either a continuous or a discrete distribution.

In combinatorics, the symbolic method is a technique for counting combinatorial objects. It uses the internal structure of the objects to derive formulas for their generating functions. The method is mostly associated with Philippe Flajolet and is detailed in Part A of his book with Robert Sedgewick, Analytic Combinatorics, while the rest of the book explains how to use complex analysis in order to get asymptotic and probabilistic results on the corresponding generating functions.

Dirichlet distribution Probability distribution

In probability and statistics, the Dirichlet distribution, often denoted $, is a family of continuous multivariate probability distributions parameterized by a vector of positive reals. It is a multivariate generalization of the beta distribution, hence its alternative name of multivariate beta distribution (MBD) . Dirichlet distributions are commonly used as prior distributions in Bayesian statistics, and in fact the Dirichlet distribution is the conjugate prior of the categorical distribution and multinomial distribution.$

In probability theory, a distribution is said to be stable if a linear combination of two independent random variables with this distribution has the same distribution, up to location and scale parameters. A random variable is said to be stable if its distribution is stable. The stable distribution family is also sometimes referred to as the Lévy alpha-stable distribution, after Paul Lévy, the first mathematician to have studied it.

A continuous-time Markov chain (CTMC) is a continuous stochastic process in which, for each state, the process will change state according to an exponential random variable and then move to a different state as specified by the probabilities of a stochastic matrix. An equivalent formulation describes the process as changing state according to the least value of a set of exponential random variables, one for each possible state it can move to, with the parameters determined by the current state.

In probability theory and statistics, the Dirichlet-multinomial distribution is a family of discrete multivariate probability distributions on a finite support of non-negative integers. It is also called the Dirichlet compound multinomial distribution (DCM) or multivariate Pólya distribution. It is a compound probability distribution, where a probability vector p is drawn from a Dirichlet distribution with parameter vector $, and an observation drawn from a multinomial distribution with probability vector p and number of trials n . The Dirichlet parameter vector captures the prior belief about the situation and can be seen as a pseudocount: observations of each outcome that occur before the actual data is collected. The compounding corresponds to a Pólya urn scheme. It is frequently encountered in Bayesian statistics, machine learning, empirical Bayes methods and classical statistics as an overdispersed multinomial distribution.$

A ratio distribution is a probability distribution constructed as the distribution of the ratio of random variables having two other known distributions. Given two random variables X and Y, the distribution of the random variable Z that is formed as the ratio Z = X/Y is a ratio distribution.

In probability and statistics, the truncated normal distribution is the probability distribution derived from that of a normally distributed random variable by bounding the random variable from either below or above. The truncated normal distribution has wide applications in statistics and econometrics. For example, it is used to model the probabilities of the binary outcomes in the probit model and to model censored data in the tobit model.

Tail value at risk (TVaR), also known as tail conditional expectation (TCE) or conditional tail expectation (CTE), is a risk measure associated with the more general value at risk. It quantifies the expected value of the loss given that an event outside a given probability level has occurred.

Financial models with long-tailed distributions and volatility clustering have been introduced to overcome problems with the realism of classical financial models. These classical models of financial time series typically assume homoskedasticity and normality cannot explain stylized phenomena such as skewness, heavy tails, and volatility clustering of the empirical asset returns in finance. In 1963, Benoit Mandelbrot first used the stable distribution to model the empirical distributions which have the skewness and heavy-tail property. Since $-stable distributions have infinite -th moments for all, the tempered stable processes have been proposed for overcoming this limitation of the stable distribution.$

A product distribution is a probability distribution constructed as the distribution of the product of random variables having two other known distributions. Given two statistically independent random variables X and Y, the distribution of the random variable Z that is formed as the product

A geometric stable distribution or geo-stable distribution is a type of leptokurtic probability distribution. Geometric stable distributions were introduced in Klebanov, L. B., Maniya, G. M., and Melamed, I. A. (1985). A problem of Zolotarev and analogs of infinitely divisible and stable distributions in a scheme for summing a random number of random variables. These distributions are analogues for stable distributions for the case when the number of summands is random, independent of the distribution of summand, and having geometric distribution. The geometric stable distribution may be symmetric or asymmetric. A symmetric geometric stable distribution is also referred to as a Linnik distribution. The Laplace distribution and asymmetric Laplace distribution are special cases of the geometric stable distribution. The Laplace distribution is also a special case of a Linnik distribution. The Mittag-Leffler distribution is also a special case of a geometric stable distribution.

The generalized functional linear model (GFLM) is an extension of the generalized linear model (GLM) that allows one to regress univariate responses of various types on functional predictors, which are mostly random trajectories generated by a square-integrable stochastic processes. Similarly to GLM, a link function relates the expected value of the response variable to a linear predictor, which in case of GFLM is obtained by forming the scalar product of the random predictor function $with a smooth parameter function . Functional Linear Regression, Functional Poisson Regression and Functional Binomial Regression, with the important Functional Logistic Regression included, are special cases of GFLM. Applications of GFLM include classification and discrimination of stochastic processes and functional data.$

References

1 2 Spitzer, F. (1956). "A combinatorial lemma and its application to probability theory". Transactions of the American Mathematical Society. 82 (2): 323–339. doi: 10.1090/S0002-9947-1956-0079851-X .
↑ Ebrahimi-Fard, K.; Guo, L.; Kreimer, D. (2004). "Spitzer's identity and the algebraic Birkhoff decomposition in pQFT". Journal of Physics A: Mathematical and General. 37 (45): 11037. arXiv: hep-th/0407082 . Bibcode:2004JPhA...3711037E. doi:10.1088/0305-4470/37/45/020.
1 2 Wendel, James G. (1958). "Spitzer's formula: A short proof". Proceedings of the American Mathematical Society. 9 (6): 905–908. doi: 10.1090/S0002-9939-1958-0103531-2 . MR 0103531.

This probability-related article is a stub. You can help Wikipedia by expanding it.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[spitzer-1] 1 2 Spitzer, F. (1956). "A combinatorial lemma and its application to probability theory". Transactions of the American Mathematical Society. 82 (2): 323–339. doi: 10.1090/S0002-9947-1956-0079851-X .

[2] Ebrahimi-Fard, K.; Guo, L.; Kreimer, D. (2004). "Spitzer's identity and the algebraic Birkhoff decomposition in pQFT". Journal of Physics A: Mathematical and General. 37 (45): 11037. arXiv: hep-th/0407082 . Bibcode:2004JPhA...3711037E. doi:10.1088/0305-4470/37/45/020.

[wendel-3] 1 2 Wendel, James G. (1958). "Spitzer's formula: A short proof". Proceedings of the American Mathematical Society. 9 (6): 905–908. doi: 10.1090/S0002-9939-1958-0103531-2 . MR 0103531.

[1]

[2]

[3]

Spitzer's formula

Contents

Statement of theorem

Proof

Related Research Articles

References