Spouge's approximation

Last updated December 16, 2020

In mathematics, Spouge's approximation is a formula for computing an approximation of the gamma function. It was named after John L. Spouge, who defined the formula in a 1994 paper.^[1] The formula is a modification of Stirling's approximation, and has the form

\Gamma (z+1)=(z+a)^{z+{\frac {1}{2}}}e^{-z-a}\left(c_{0}+\sum _{k=1}^{a-1}{\frac {c_{k}}{z+k}}+\varepsilon _{a}(z)\right)

where a is an arbitrary positive integer and the coefficients are given by

{\begin{aligned}c_{0}&={\sqrt {2\pi }}\\c_{k}&={\frac {(-1)^{k-1}}{(k-1)!}}(-k+a)^{k-{\frac {1}{2}}}e^{-k+a}\qquad k\in \{1,2,\dots ,a-1\}.\end{aligned}}

Spouge has proved that, if Re(z) > 0 and a > 2, the relative error in discarding ε_a(z) is bounded by

a^{-{\frac {1}{2}}}(2\pi )^{-a-{\frac {1}{2}}}.

The formula is similar to the Lanczos approximation, but has some distinct features^[2]. Whereas the Lanczos formula exhibits faster convergence, Spouge's coefficients are much easier to calculate and the error can be set arbitrarily low. The formula is therefore feasible for arbitrary-precision evaluation of the gamma function. However, special care must be taken to use sufficient precision when computing the sum due to the large size of the coefficients c_k, as well as their alternating sign. For example, for a = 49, one must compute the sum using about 65 decimal digits of precision in order to obtain the promised 40 decimal digits of accuracy.

Related Research Articles

In mathematics, the binomial coefficients are the positive integers that occur as coefficients in the binomial theorem. Commonly, a binomial coefficient is indexed by a pair of integers $n \geq k \geq 0$ and is written $It is the coefficient of the x k term in the polynomial expansion of the binomial power (1 + x) n, and is given by the formula$

In mathematics, the factorial of a positive integer $n$ , denoted by $n!$ , is the product of all positive integers less than or equal to $n$ :

In mathematics, the gamma function is one commonly used extension of the factorial function to complex numbers. The gamma function is defined for all complex numbers except the non-positive integers. For any positive integer $n$ ,

The number $π$ is a mathematical constant. It is defined as the ratio of a circle's circumference to its diameter, and it also has various equivalent definitions. It appears in many formulas in all areas of mathematics and physics. It is approximately equal to 3.14159. It has been represented by the Greek letter " $π$ " since the mid-18th century, and is spelled out as "pi". It is also referred to as Archimedes' constant.

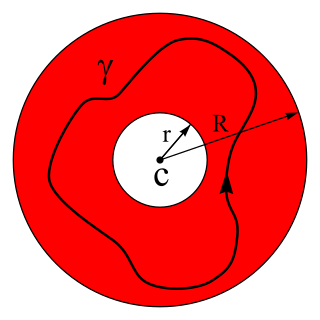
In mathematics, the Laurent series of a complex function f(z) is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where a Taylor series expansion cannot be applied. The Laurent series was named after and first published by Pierre Alphonse Laurent in 1843. Karl Weierstrass may have discovered it first in a paper written in 1841, but it was not published until after his death.

Euler–Mascheroni constant γ ≈ 0.5772, the limit of the difference between the harmonic series and the natural logarithm

The Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter gamma.

In mathematics, Stirling's approximation is an approximation for factorials. It is a good approximation, leading to accurate results even for small values of $n$ . It is named after James Stirling, though it was first stated by Abraham de Moivre.

In mathematics, the error function, often denoted by erf, is a complex function of a complex variable defined as:

In mathematics, the beta function, also called the Euler integral of the first kind, is a special function that is closely related to the gamma function and to binomial coefficients. It is defined by the integral

In the physical sciences, the Airy functionAi(x) is a special function named after the British astronomer George Biddell Airy (1801–1892). The function Ai(x) and the related function Bi(x), are linearly independent solutions to the differential equation

In mathematics, the digamma function is defined as the logarithmic derivative of the gamma function:

Variational Bayesian methods are a family of techniques for approximating intractable integrals arising in Bayesian inference and machine learning. They are typically used in complex statistical models consisting of observed variables as well as unknown parameters and latent variables, with various sorts of relationships among the three types of random variables, as might be described by a graphical model. As typical in Bayesian inference, the parameters and latent variables are grouped together as "unobserved variables". Variational Bayesian methods are primarily used for two purposes:

To provide an analytical approximation to the posterior probability of the unobserved variables, in order to do statistical inference over these variables.
To derive a lower bound for the marginal likelihood of the observed data. This is typically used for performing model selection, the general idea being that a higher marginal likelihood for a given model indicates a better fit of the data by that model and hence a greater probability that the model in question was the one that generated the data.

In mathematics, the Leibniz formula for $π$ , named after Gottfried Leibniz, states that

In mathematics, the Lanczos approximation is a method for computing the gamma function numerically, published by Cornelius Lanczos in 1964. It is a practical alternative to the more popular Stirling's approximation for calculating the gamma function with fixed precision.

In mathematics, at the intersection of number theory and special functions, Apéry's constant is the sum of the reciprocals of the positive cubes. That is, it is defined as the number

The Fransén–Robinson constant, sometimes denoted F, is the mathematical constant that represents the area between the graph of the reciprocal Gamma function, $1/Γ(x)$ , and the positive x axis. That is,

In mathematics, the reciprocal gamma function is the function

Approximations for the mathematical constant pi in the history of mathematics reached an accuracy within 0.04% of the true value before the beginning of the Common Era (Archimedes). In Chinese mathematics, this was improved to approximations correct to what corresponds to about seven decimal digits by the 5th century.

In mathematics, the sine is a trigonometric function of an angle. The sine of an acute angle is defined in the context of a right triangle: for the specified angle, it is the ratio of the length of the side that is opposite that angle, to the length of the longest side of the triangle. For an angle $, the sine function is denoted simply as .$

Gregory coefficients $G n$ , also known as reciprocal logarithmic numbers, Bernoulli numbers of the second kind, or Cauchy numbers of the first kind, are the rational numbers that occur in the Maclaurin series expansion of the reciprocal logarithm

References

↑ Spouge, John L. (1994). "Computation of the Gamma, Digamma, and Trigamma Functions" (PDF). SIAM Journal on Numerical Analysis. 31 (3): 931–000. doi:10.1137/0731050. JSTOR 2158038.
↑
- Pugh, Glendon (2004). An analysis of the Lanczos Gamma approximation (PDF) (PhD thesis).

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Spouge, John L. (1994). "Computation of the Gamma, Digamma, and Trigamma Functions" (PDF). SIAM Journal on Numerical Analysis. 31 (3): 931–000. doi:10.1137/0731050. JSTOR 2158038.

[2] 
Pugh, Glendon (2004). An analysis of the Lanczos Gamma approximation (PDF) (PhD thesis).

[mwRA] Pugh, Glendon (2004). An analysis of the Lanczos Gamma approximation (PDF) (PhD thesis).

[1]

[2]

Spouge's approximation

See also

Related Research Articles

References