In control theory, and especially stability theory, a stability criterion establishes when a system is stable. A number of stability criteria are in common use:
Control theory in control systems engineering is a subfield of mathematics that deals with the control of continuously operating dynamical systems in engineered processes and machines. The objective is to develop a control model for controlling such systems using a control action in an optimum manner without delay or overshoot and ensuring control stability.

In mathematics, stability theory addresses the stability of solutions of differential equations and of trajectories of dynamical systems under small perturbations of initial conditions. The heat equation, for example, is a stable partial differential equation because small perturbations of initial data lead to small variations in temperature at a later time as a result of the maximum principle. In partial differential equations one may measure the distances between functions using Lp norms or the sup norm, while in differential geometry one may measure the distance between spaces using the Gromov–Hausdorff distance.
In the context of the characteristic polynomial of a differential equation or difference equation, a polynomial is said to be stable if either:
- Circle criterion
- Jury stability criterion
- Liénard–Chipart criterion
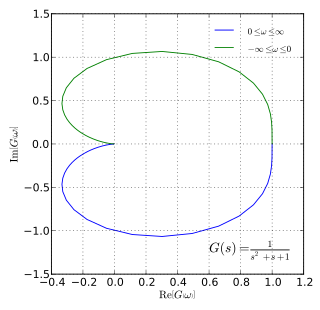
- Nyquist stability criterion
- Routh–Hurwitz stability criterion
- Vakhitov–Kolokolov stability criterion
- Barkhausen stability criterion
In nonlinear control and stability theory, the circle criterion is a stability criterion for nonlinear time-varying systems. It can be viewed as a generalization of the Nyquist stability criterion for linear time-invariant (LTI) systems.
In signal processing and control theory, the Jury stability criterion is a method of determining the stability of a linear discrete time system by analysis of the coefficients of its characteristic polynomial. It is the discrete time analogue of the Routh–Hurwitz stability criterion. The Jury stability criterion requires that the system poles are located inside the unit circle centered at the origin, while the Routh-Hurwitz stability criterion requires that the poles are in the left half of the complex plane. The Jury criterion is named after Eliahu Ibraham Jury.
In control system theory, the Liénard–Chipart criterion is a stability criterion modified from the Routh–Hurwitz stability criterion, proposed by A. Liénard and M. H. Chipart. This criterion has a computational advantage over the Routh–Hurwitz criterion because it involves only about half the number of determinant computations.
Stability may also be determined by means of root locus analysis.

In control theory and stability theory, root locus analysis is a graphical method for examining how the roots of a system change with variation of a certain system parameter, commonly a gain within a feedback system. This is a technique used as a stability criterion in the field of classical control theory developed by Walter R. Evans which can determine stability of the system. The root locus plots the poles of the closed loop transfer function in the complex s-plane as a function of a gain parameter.
Although the concept of stability is general, there are several narrower definitions through which it may be assessed:
In signal processing, specifically control theory, bounded-input, bounded-output (BIBO) stability is a form of stability for linear signals and systems that take inputs. If a system is BIBO stable, then the output will be bounded for every input to the system that is bounded.
In mathematics, in the theory of differential equations and dynamical systems, a particular stationary or quasistationary solution to a nonlinear system is called linearly unstable if the linearization of the equation at this solution has the form , where A is a linear operator whose spectrum contains eigenvalues with positive real part. If all the eigenvalues have negative real part, then the solution is called linearlystable. Other names for linear stability include exponential stability or stability in terms of first approximation. If there exist an eigenvalue with zero real part then the question about stability cannot be solved on the basis of the first approximation and we approach the so-called "centre and focus problem".
Various types of stability may be discussed for the solutions of differential equations or difference equations describing dynamical systems. The most important type is that concerning the stability of solutions near to a point of equilibrium. This may be discussed by the theory of Lyapunov. In simple terms, if the solutions that start out near an equilibrium point stay near forever, then is Lyapunov stable. More strongly, if is Lyapunov stable and all solutions that start out near converge to , then is asymptotically stable. The notion of exponential stability guarantees a minimal rate of decay, i.e., an estimate of how quickly the solutions converge. The idea of Lyapunov stability can be extended to infinite-dimensional manifolds, where it is known as structural stability, which concerns the behavior of different but "nearby" solutions to differential equations. Input-to-state stability (ISS) applies Lyapunov notions to systems with inputs.
| This article includes a list of related items that share the same name (or similar names). If an internal link incorrectly led you here, you may wish to change the link to point directly to the intended article. |