Stanley symmetric function

Last updated February 24, 2019

In mathematics and especially in algebraic combinatorics, the Stanley symmetric functions are a family of symmetric polynomials introduced by RichardStanley ( 1984 ) in his study of the symmetric group of permutations.

Mathematics includes the study of such topics as quantity, structure, space, and change.

Algebraic combinatorics is an area of mathematics that employs methods of abstract algebra, notably group theory and representation theory, in various combinatorial contexts and, conversely, applies combinatorial techniques to problems in algebra.

In mathematics, a symmetric polynomial is a polynomial $P (X 1, X 2, \dots, X n)$ in $n$ variables, such that if any of the variables are interchanged, one obtains the same polynomial. Formally, $P$ is a symmetric polynomial if for any permutation $σ$ of the subscripts $1, 2, ..., n$ one has $P (X σ, X σ, \dots, X σ) = P (X 1, X 2, \dots, X n)$ .

Formally, the Stanley symmetric function F_w(x₁, x₂, ...) indexed by a permutation w is defined as a sum of certain fundamental quasisymmetric functions. Each summand corresponds to a reduced decomposition of w, that is, to a way of writing w as a product of a minimal possible number of adjacent transpositions. They were introduced in the course of Stanley's enumeration of the reduced decompositions of permutations, and in particular his proof that the permutation w₀ = n(n− 1)...21 (written here in one-line notation) has exactly

{\frac {{\binom {n}{2}}!}{1^{n-1}\cdot 3^{n-2}\cdot 5^{n-3}\cdots (2n-3)^{1}}}

reduced decompositions. (Here ${\binom {n}{2}}$ denotes the binomial coefficient n(n− 1)/2 and ! denotes the factorial.)

In mathematics, the binomial coefficients are the positive integers that occur as coefficients in the binomial theorem. Commonly, a binomial coefficient is indexed by a pair of integers $n \geq k \geq 0$ and is written $It is the coefficient of the x k term in the polynomial expansion of the binomial power (1 + x) n, and it is given by the formula$

In mathematics, the factorial of a positive integer $n$ , denoted by $n!$ , is the product of all positive integers less than or equal to $n$ . For example,

Properties

The Stanley symmetric function F_w is homogeneous with degree equal to the number of inversions of w. Unlike other nice families of symmetric functions, the Stanley symmetric functions have many linear dependencies and so do not form a basis of the ring of symmetric functions. When a Stanley symmetric function is expanded in the basis of Schur functions, the coefficients are all non-negative integers.

In mathematics, a homogeneous polynomial is a polynomial whose nonzero terms all have the same degree. For example, $is a homogeneous polynomial of degree 5, in two variables; the sum of the exponents in each term is always 5. The polynomial is not homogeneous, because the sum of exponents does not match from term to term. A polynomial is homogeneous if and only if it defines a homogeneous function. An algebraic form, or simply form, is a function defined by a homogeneous polynomial. A binary form is a form in two variables. A form is also a function defined on a vector space, which may be expressed as a homogeneous function of the coordinates over any basis.$

The degree of a polynomial is the highest degree of its monomials with non-zero coefficients. The degree of a term is the sum of the exponents of the variables that appear in it, and thus is a non-negative integer. The term order has been used as a synonym of degree but, nowadays, may refer to several other concepts . For example, the polynomial $which can also be expressed as has three terms. The first term has a degree of 5, the second term has a degree of 1, and the last term has a degree of 0. Therefore, the polynomial has a degree of 5, which is the highest degree of any term.$

In computer science and discrete mathematics a sequence has an inversion where two of its elements are out of their natural order.

The Stanley symmetric functions have the property that they are the stable limit of Schubert polynomials

F_{w}(x)=\lim _{n\to \infty }{\mathfrak {S}}_{1^{n}\times w}(x)

where we treat both sides as formal power series, and take the limit coefficientwise.

Related Research Articles

In abstract algebra, the symmetric group defined over any set is the group whose elements are all the bijections from the set to itself, and whose group operation is the composition of functions. In particular, the finite symmetric group S_n defined over a finite set of n symbols consists of the permutation operations that can be performed on the n symbols. Since there are n! possible permutation operations that can be performed on a tuple composed of n symbols, it follows that the number of elements of the symmetric group S_n is n!.

In mathematics, a generating function is a way of encoding an infinite sequence of numbers (a_n) by treating them as the coefficients of a power series. This formal power series is the generating function. Unlike an ordinary series, this formal series is allowed to diverge, meaning that the generating function is not always a true function and the "variable" is actually an indeterminate. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general linear recurrence problem. One can generalize to formal series in more than one indeterminate, to encode information about arrays of numbers indexed by several natural numbers.

In mathematics, the falling factorial is defined as the polynomial

In algebra, the partial fraction decomposition or partial fraction expansion of a rational function is an operation that consists of expressing the fraction as a sum of a polynomial and one or several fractions with a simpler denominator.

In combinatorics, the inclusion–exclusion principle is a counting technique which generalizes the familiar method of obtaining the number of elements in the union of two finite sets; symbolically expressed as

In mathematics, and in particular in group theory, a cyclic permutation is a permutation of the elements of some set X which maps the elements of some subset S of X to each other in a cyclic fashion, while fixing all other elements of X. If S has k elements, the cycle is called a k-cycle.

In mathematics, specifically in commutative algebra, the elementary symmetric polynomials are one type of basic building block for symmetric polynomials, in the sense that any symmetric polynomial can be expressed as a polynomial in elementary symmetric polynomials. That is, any symmetric polynomial $P$ is given by an expression involving only additions and multiplication of constants and elementary symmetric polynomials. There is one elementary symmetric polynomial of degree $d$ in $n$ variables for each nonnegative integer $d \leq n$ , and it is formed by adding together all distinct products of $d$ distinct variables.

In mathematics, a q-analog of a theorem, identity or expression is a generalization involving a new parameter q that returns the original theorem, identity or expression in the limit as $q \to 1$ . Typically, mathematicians are interested in q-analogs that arise naturally, rather than in arbitrarily contriving q-analogs of known results. The earliest q-analog studied in detail is the basic hypergeometric series, which was introduced in the 19th century.

In combinatorics, the Eulerian numberA(n, m), is the number of permutations of the numbers 1 to n in which exactly m elements are greater than the previous element. They are the coefficients of the Eulerian polynomials:

The Stanley–Wilf conjecture, formulated independently by Richard P. Stanley and Herbert Wilf in the late 1980s, states that the growth rate of every proper permutation class is singly exponential. It was proved by Adam Marcus and Gábor Tardos (2004) and is no longer a conjecture. Marcus and Tardos actually proved a different conjecture, due to Zoltán Füredi and Péter Hajnal (1992), which had been shown to imply the Stanley–Wilf conjecture by Klazar (2000).

In mathematics, specifically in commutative algebra, the power sum symmetric polynomials are a type of basic building block for symmetric polynomials, in the sense that every symmetric polynomial with rational coefficients can be expressed as a sum and difference of products of power sum symmetric polynomials with rational coefficients. However, not every symmetric polynomial with integral coefficients is generated by integral combinations of products of power-sum polynomials: they are a generating set over the rationals, but not over the integers.

In combinatorial mathematics, a rook polynomial is a generating polynomial of the number of ways to place non-attacking rooks on a board that looks like a checkerboard; that is, no two rooks may be in the same row or column. The board is any subset of the squares of a rectangular board with m rows and n columns; we think of it as the squares in which one is allowed to put a rook. The board is the ordinary chessboard if all squares are allowed and m = n = 8 and a chessboard of any size if all squares are allowed and m = n. The coefficient of x^k in the rook polynomial R_B(x) is the number of ways k rooks, none of which attacks another, can be arranged in the squares of B. The rooks are arranged in such a way that there is no pair of rooks in the same row or column. In this sense, an arrangement is the positioning of rooks on a static, immovable board; the arrangement will not be different if the board is rotated or reflected while keeping the squares stationary. The polynomial also remains the same if rows are interchanged or columns are interchanged.

In mathematics, a symmetric tensor is a tensor that is invariant under a permutation of its vector arguments:

In combinatorial mathematics and theoretical computer science, a permutation pattern is a sub-permutation of a longer permutation. Any permutation may be written in one-line notation as a sequence of digits representing the result of applying the permutation to the digit sequence 123...; for instance the digit sequence 213 represents the permutation on three elements that swaps elements 1 and 2. If π and σ are two permutations represented in this way, then π is said to contain σ as a pattern if some subsequence of the digits of π has the same relative order as all of the digits of σ.

In algebra and in particular in algebraic combinatorics, a quasisymmetric function is any element in the ring of quasisymmetric functions which is in turn a subring of the formal power series ring with a countable number of variables. This ring generalizes the ring of symmetric functions. This ring can be realized as a specific limit of the rings of quasisymmetric polynomials in n variables, as n goes to infinity. This ring serves as universal structure in which relations between quasisymmetric polynomials can be expressed in a way independent of the number n of variables.

In mathematics, Schubert polynomials are generalizations of Schur polynomials that represent cohomology classes of Schubert cycles in flag varieties. They were introduced by Lascoux & Schützenberger (1982) and are named after Hermann Schubert.

In combinatorial mathematics, the hook-length formula is a formula for the number of standard Young tableaux whose shape is a given Young diagram. It has applications in diverse areas such as representation theory, probability, and algorithm analysis; for example, the problem of longest increasing subsequences.

Plethystic substitution is a shorthand notation for a common kind of substitution in the algebra of symmetric functions and that of symmetric polynomials. It is essentially basic substitution of variables, but allows for a change in the number of variables used.

References

Stanley, Richard P. (1984), "On the number of reduced decompositions of elements of Coxeter groups" (PDF), European Journal of Combinatorics, 5 (4): 359–372, doi:10.1016/s0195-6698(84)80039-6, ISSN 0195-6698, MR 0782057

In computing, a Digital Object Identifier orDOI is a persistent identifier or handle used to uniquely identify objects, standardized by the International Organization for Standardization (ISO). An implementation of the Handle System, DOIs are in wide use mainly to identify academic, professional, and government information, such as journal articles, research reports and data sets, and official publications though they also have been used to identify other types of information resources, such as commercial videos.

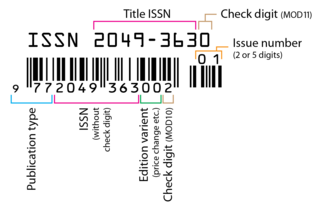
International Standard Serial Number unique eight-digit number used to identify a print or electronic periodical publication

An International Standard Serial Number (ISSN) is an eight-digit serial number used to uniquely identify a serial publication, such as a magazine. The ISSN is especially helpful in distinguishing between serials with the same title. ISSN are used in ordering, cataloging, interlibrary loans, and other practices in connection with serial literature.

Mathematical Reviews is a journal published by the American Mathematical Society (AMS) that contains brief synopses, and in some cases evaluations, of many articles in mathematics, statistics, and theoretical computer science. The AMS also publishes an associated online bibliographic database called MathSciNet which contains an electronic version of Mathematical Reviews and additionally contains citation information for over 3.5 million items as of 2018.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.