In theoretical computer science and formal language theory, a regular language is a formal language that can be defined by a regular expression, in the strict sense in theoretical computer science.
In mathematics and computer science, the Krohn–Rhodes theory is an approach to the study of finite semigroups and automata that seeks to decompose them in terms of elementary components. These components correspond to finite aperiodic semigroups and finite simple groups that are combined in a feedback-free manner.

In the theory of computation, a branch of theoretical computer science, a deterministic finite automaton (DFA)—also known as deterministic finite acceptor (DFA), deterministic finite-state machine (DFSM), or deterministic finite-state automaton (DFSA)—is a finite-state machine that accepts or rejects a given string of symbols, by running through a state sequence uniquely determined by the string. Deterministic refers to the uniqueness of the computation run. In search of the simplest models to capture finite-state machines, Warren McCulloch and Walter Pitts were among the first researchers to introduce a concept similar to finite automata in 1943.
In automata theory, a finite-state machine is called a deterministic finite automaton (DFA), if
In automata theory, an alternating finite automaton (AFA) is a nondeterministic finite automaton whose transitions are divided into existential and universal transitions. For example, let A be an alternating automaton.
In the theory of computation and automata theory, the powerset construction or subset construction is a standard method for converting a nondeterministic finite automaton (NFA) into a deterministic finite automaton (DFA) which recognizes the same formal language. It is important in theory because it establishes that NFAs, despite their additional flexibility, are unable to recognize any language that cannot be recognized by some DFA. It is also important in practice for converting easier-to-construct NFAs into more efficiently executable DFAs. However, if the NFA has n states, the resulting DFA may have up to 2n states, an exponentially larger number, which sometimes makes the construction impractical for large NFAs.
In computer science, in particular in automata theory, a two-way finite automaton is a finite automaton that is allowed to re-read its input.
Language equations are mathematical statements that resemble numerical equations, but the variables assume values of formal languages rather than numbers. Instead of arithmetic operations in numerical equations, the variables are joined by language operations. Among the most common operations on two languages A and B are the set union A ∪ B, the set intersection A ∩ B, and the concatenation A⋅B. Finally, as an operation taking a single operand, the set A* denotes the Kleene star of the language A. Therefore, language equations can be used to represent formal grammars, since the languages generated by the grammar must be the solution of a system of language equations.
In mathematics and computer science, the probabilistic automaton (PA) is a generalization of the nondeterministic finite automaton; it includes the probability of a given transition into the transition function, turning it into a transition matrix. Thus, the probabilistic automaton also generalizes the concepts of a Markov chain and of a subshift of finite type. The languages recognized by probabilistic automata are called stochastic languages; these include the regular languages as a subset. The number of stochastic languages is uncountable.
A read-only Turing machine or two-way deterministic finite-state automaton (2DFA) is class of models of computability that behave like a standard Turing machine and can move in both directions across input, except cannot write to its input tape. The machine in its bare form is equivalent to a deterministic finite automaton in computational power, and therefore can only parse a regular language.
In computer science, a pebble automaton is any variant of an automaton which augments the original model with a finite number of "pebbles" that may be used to mark tape positions.

In automata theory, DFA minimization is the task of transforming a given deterministic finite automaton (DFA) into an equivalent DFA that has a minimum number of states. Here, two DFAs are called equivalent if they recognize the same regular language. Several different algorithms accomplishing this task are known and described in standard textbooks on automata theory.
In graph theory, the cycle rank of a directed graph is a digraph connectivity measure proposed first by Eggan and Büchi. Intuitively, this concept measures how close a digraph is to a directed acyclic graph (DAG), in the sense that a DAG has cycle rank zero, while a complete digraph of order n with a self-loop at each vertex has cycle rank n. The cycle rank of a directed graph is closely related to the tree-depth of an undirected graph and to the star height of a regular language. It has also found use in sparse matrix computations and logic (Rossman 2008).
In mathematics, a local language is a formal language for which membership of a word in the language can be determined by looking at the first and last symbol and each two-symbol substring of the word. Equivalently, it is a language recognised by a local automaton, a particular kind of deterministic finite automaton.
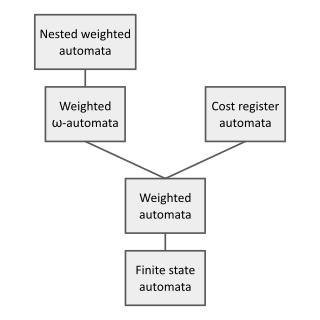
In theoretical computer science and formal language theory, a weighted automaton or weighted finite-state machine is a generalization of a finite-state machine in which the edges have weights, for example real numbers or integers. Finite-state machines are only capable of answering decision problems; they take as input a string and produce a Boolean output, i.e. either "accept" or "reject". In contrast, weighted automata produce a quantitative output, for example a count of how many answers are possible on a given input string, or a probability of how likely the input string is according to a probability distribution. They are one of the simplest studied models of quantitative automata.
In automata theory, an unambiguous finite automaton (UFA) is a nondeterministic finite automaton (NFA) such that each word has at most one accepting path. Each deterministic finite automaton (DFA) is an UFA, but not vice versa. DFA, UFA, and NFA recognize exactly the same class of formal languages. On the one hand, an NFA can be exponentially smaller than an equivalent DFA. On the other hand, some problems are easily solved on DFAs and not on UFAs. For example, given an automaton A, an automaton A′ which accepts the complement of A can be computed in linear time when A is a DFA, whereas it is known that this cannot be done in polynomial time for UFAs. Hence UFAs are a mix of the worlds of DFA and of NFA; in some cases, they lead to smaller automata than DFA and quicker algorithms than NFA.

Kai Tapani Salomaa is a Finnish Canadian theoretical computer scientist, known for his numerous contributions to the state complexity of finite automata. His highly cited 1994 joint paper with Yu and Zhuang laid the foundations of the area. He has published over 100 papers in scientific journals on various subjects in formal language theory. Salomaa is a full professor at Queen's University.
In automata theory, a self-verifying finite automaton (SVFA) is a special kind of a nondeterministic finite automaton (NFA) with a symmetric kind of nondeterminism introduced by Hromkovič and Schnitger. Generally, in self-verifying nondeterminism, each computation path is concluded with any of the three possible answers: yes, no, and I do not know. For each input string, no two paths may give contradictory answers, namely both answers yes and no on the same input are not possible. At least one path must give answer yes or no, and if it is yes then the string is considered accepted. SVFA accept the same class of languages as deterministic finite automata (DFA) and NFA but have different state complexity.
Giovanni Pighizzini is an Italian theoretical computer scientist known for his work in formal language theory and particularly in state complexity of two-way finite automata. He earned his PhD in 1993 from the University of Milan, where he is a full professor since 2001. Pighizzini serves as the Steering Committee Chair of the annual Descriptional Complexity of Formal Systems academic conference since 2006.
In theoretical computer science and formal language theory, the complementation of an automaton is the problem of computing an automaton that accepts precisely the words rejected by another automaton. Formally, given an automaton A which recognizes a regular language L, we want to compute an automaton recognizing precisely the words that are not in L, i.e., the complement of L.































































