In number theory, two integers a and b are said to be relatively prime, mutually prime, or coprime if the only positive integer (factor) that divides both of them is 1. Consequently, any prime number that divides one does not divide the other. This is equivalent to their greatest common divisor (gcd) being 1.

In mathematics, a square root of a number x is a number y such that y2 = x; in other words, a number y whose square (the result of multiplying the number by itself, or y ⋅ y) is x. For example, 4 and −4 are square roots of 16 because 42 = (−4)2 = 16. Every nonnegative real number x has a unique nonnegative square root, called the principal square root, which is denoted by √x, where the symbol √ is called the radical sign or radix. For example, the principal square root of 9 is 3, which is denoted by √9 = 3, because 32 = 3 ⋅ 3 = 9 and 3 is nonnegative. The term (or number) whose square root is being considered is known as the radicand. The radicand is the number or expression underneath the radical sign, in this example 9.
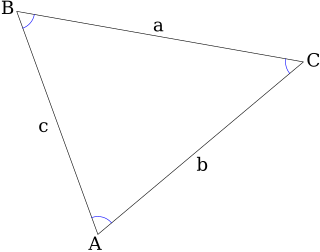
In trigonometry, the law of sines, sine law, sine formula, or sine rule is an equation relating the lengths of the sides of a triangle to the sines of its angles. According to the law,

Ceva's theorem is a theorem about triangles in plane geometry. Given a triangle ABC, let the lines AO, BO and CO be drawn from the vertices to a common point O, to meet opposite sides at D, E and F respectively. Then, using signed lengths of segments,

In geometry, a heptadecagon or 17-gon is a seventeen-sided polygon.
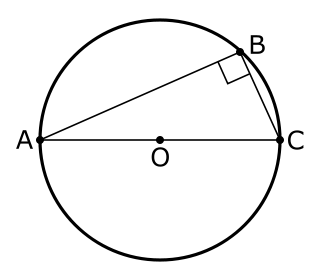
In geometry, Thales's theorem states that if A, B, and C are distinct points on a circle where the line AC is a diameter, then the angle ∠ABC is a right angle. Thales' theorem is a special case of the inscribed angle theorem, and is mentioned and proved as part of the 31st proposition, in the third book of Euclid's Elements. It is generally attributed to Thales of Miletus, who is said to have offered an ox as a sacrifice of thanksgiving for the discovery, but sometimes it is attributed to Pythagoras.

Computational fluid dynamics (CFD) is a branch of fluid mechanics that uses numerical analysis and data structures to analyze and solve problems that involve fluid flows. Computers are used to perform the calculations required to simulate the free-stream flow of the fluid, and the interaction of the fluid with surfaces defined by boundary conditions. With high-speed supercomputers, better solutions can be achieved, and are often required to solve the largest and most complex problems. Ongoing research yields software that improves the accuracy and speed of complex simulation scenarios such as transonic or turbulent flows. Initial validation of such software is typically performed using experimental apparatus such as wind tunnels. In addition, previously performed analytical or empirical analysis of a particular problem can be used for comparison. A final validation is often performed using full-scale testing, such as flight tests.
Shape optimization is part of the field of optimal control theory. The typical problem is to find the shape which is optimal in that it minimizes a certain cost functional while satisfying given constraints. In many cases, the functional being solved depends on the solution of a given partial differential equation defined on the variable domain.

Menelaus's theorem, named for Menelaus of Alexandria, is a proposition about triangles in plane geometry. Given a triangle ABC, and a transversal line that crosses BC, AC, and AB at points D, E, and F respectively, with D, E, and F distinct from A, B, and C, then
Named after the 19th century British mathematician Arthur Cayley, a Cayley table describes the structure of a finite group by arranging all the possible products of all the group's elements in a square table reminiscent of an addition or multiplication table. Many properties of a group – such as whether or not it is abelian, which elements are inverses of which elements, and the size and contents of the group's center – can be discovered from its Cayley table.

The Peaucellier–Lipkin linkage, invented in 1864, was the first true planar straight line mechanism – the first planar linkage capable of transforming rotary motion into perfect straight-line motion, and vice versa. It is named after Charles-Nicolas Peaucellier (1832–1913), a French army officer, and Yom Tov Lipman Lipkin (1846–1876), a Lithuanian Jew and son of the famed Rabbi Israel Salanter.

In computer science and electrical engineering, Lloyd's algorithm, also known as Voronoi iteration or relaxation, is an algorithm named after Stuart P. Lloyd for finding evenly spaced sets of points in subsets of Euclidean spaces and partitions of these subsets into well-shaped and uniformly sized convex cells. Like the closely related k-means clustering algorithm, it repeatedly finds the centroid of each set in the partition and then re-partitions the input according to which of these centroids is closest. In this setting, the mean operation is an integral over a region of space, and the nearest centroid operation results in Voronoi diagrams.

Mesh generation is the practice of creating a mesh, a subdivision of a continuous geometric space into discrete geometric and topological cells. Often these cells form a simplicial complex. Usually the cells partition the geometric input domain. Mesh cells are used as discrete local approximations of the larger domain. Meshes are created by computer algorithms, often with human guidance through a GUI, depending on the complexity of the domain and the type of mesh desired. The goal is to create a mesh that accurately captures the input domain geometry, with high-quality (well-shaped) cells, and without so many cells as to make subsequent calculations intractable. The mesh should also be fine in areas that are important for the subsequent calculations.

The finite element method (FEM) is the most widely used method for solving problems of engineering and mathematical models. Typical problem areas of interest include the traditional fields of structural analysis, heat transfer, fluid flow, mass transport, and electromagnetic potential. The FEM is a particular numerical method for solving partial differential equations in two or three space variables. To solve a problem, the FEM subdivides a large system into smaller, simpler parts that are called finite elements. This is achieved by a particular space discretisation in the space dimensions, which is implemented by the construction of a mesh of the object: the numerical domain for the solution, which has a finite number of points. The finite element method formulation of a boundary value problem finally results in a system of algebraic equations. The method approximates the unknown function over the domain. The simple equations that model these finite elements are then assembled into a larger system of equations that models the entire problem. The FEM then uses variational methods from the calculus of variations to approximate a solution by minimizing an associated error function.
Mass point geometry, colloquially known as mass points, is a geometry problem-solving technique which applies the physical principle of the center of mass to geometry problems involving triangles and intersecting cevians. All problems that can be solved using mass point geometry can also be solved using either similar triangles, vectors, or area ratios, but many students prefer to use mass points. Though modern mass point geometry was developed in the 1960s by New York high school students, the concept has been found to have been used as early as 1827 by August Ferdinand Möbius in his theory of homogeneous coordinates.

CD-adapco was a multinational computer software company that authors and distributes applications used for computer-aided engineering, best known for its computational fluid dynamics (CFD) products.
Fluid motion is governed by the Navier–Stokes equations, a set of coupled and nonlinear partial differential equations derived from the basic laws of conservation of mass, momentum and energy. The unknowns are usually the flow velocity, the pressure and density and temperature. The analytical solution of this equation is impossible hence scientists resort to laboratory experiments in such situations. The answers delivered are, however, usually qualitatively different since dynamical and geometric similitude are difficult to enforce simultaneously between the lab experiment and the prototype. Furthermore, the design and construction of these experiments can be difficult, particularly for stratified rotating flows. Computational fluid dynamics (CFD) is an additional tool in the arsenal of scientists. In its early days CFD was often controversial, as it involved additional approximation to the governing equations and raised additional (legitimate) issues. Nowadays CFD is an established discipline alongside theoretical and experimental methods. This position is in large part due to the exponential growth of computer power which has allowed us to tackle ever larger and more complex problems.

In triangle geometry, an inellipse is an ellipse that touches the three sides of a triangle. The simplest example is the incircle. Further important inellipses are the Steiner inellipse, which touches the triangle at the midpoints of its sides, the Mandart inellipse and Brocard inellipse. For any triangle there exist an infinite number of inellipses.
FEATool Multiphysics is a physics, finite element analysis (FEA), and PDE simulation toolbox. FEATool Multiphysics features the ability to model fully coupled heat transfer, fluid dynamics, chemical engineering, structural mechanics, fluid-structure interaction (FSI), electromagnetics, as well as user-defined and custom PDE problems in 1D, 2D (axisymmetry), or 3D, all within a simple graphical user interface (GUI) or optionally as convenient script files. Having specifically been designed to have a low learning curve and to be able to be used without requiring reading documentation, FEATool has been employed and used in academic research, teaching, and industrial engineering simulation contexts.















