Stewart's theorem

Last updated November 04, 2024

In geometry, Stewart's theorem yields a relation between the lengths of the sides and the length of a cevian in a triangle. Its name is in honour of the Scottish mathematician Matthew Stewart, who published the theorem in 1746.^[1]

Statement

Let $a$ , $b$ , $c$ be the lengths of the sides of a triangle. Let $d$ be the length of a cevian to the side of length $a$ . If the cevian divides the side of length $a$ into two segments of length $m$ and $n$ , with $m$ adjacent to $c$ and $n$ adjacent to $b$ , then Stewart's theorem states that $b^{2}m+c^{2}n=a(d^{2}+mn).$

A common mnemonic used by students to memorize this equation (after rearranging the terms) is: ${\underset {{\text{A }}man{\text{ and his }}dad}{man\ +\ dad}}=\!\!\!\!\!\!{\underset {{\text{put a }}bomb{\text{ in the }}sink.}{bmb\ +\ cnc}}$

The theorem may be written more symmetrically using signed lengths of segments. That is, take the length $AB$ to be positive or negative according to whether $A$ is to the left or right of $B$ in some fixed orientation of the line. In this formulation, the theorem states that if $A, B, C$ are collinear points, and $P$ is any point, then

\left({\overline {PA}}^{2}\cdot {\overline {BC}}\right)+\left({\overline {PB}}^{2}\cdot {\overline {CA}}\right)+\left({\overline {PC}}^{2}\cdot {\overline {AB}}\right)+\left({\overline {AB}}\cdot {\overline {BC}}\cdot {\overline {CA}}\right)=0.

^[2]

In the special case where the cevian is a median (meaning it divides the opposite side into two segments of equal length), the result is known as Apollonius' theorem.

Proof

The theorem can be proved as an application of the law of cosines.^[3]

Let $θ$ be the angle between $m$ and $d$ and $θ'$ the angle between $n$ and $d$ . Then $θ'$ is the supplement of $θ$ , and so $cos θ' = -cos θ$ . Applying the law of cosines in the two small triangles using angles $θ$ and $θ'$ produces ${\begin{aligned}c^{2}&=m^{2}+d^{2}-2dm\cos \theta ,\\b^{2}&=n^{2}+d^{2}-2dn\cos \theta '\\&=n^{2}+d^{2}+2dn\cos \theta .\end{aligned}}$

Multiplying the first equation by $n$ and the third equation by $m$ and adding them eliminates $cos θ$ . One obtains ${\begin{aligned}b^{2}m+c^{2}n&=nm^{2}+n^{2}m+(m+n)d^{2}\\&=(m+n)(mn+d^{2})\\&=a(mn+d^{2}),\\\end{aligned}}$ which is the required equation.

Alternatively, the theorem can be proved by drawing a perpendicular from the vertex of the triangle to the base and using the Pythagorean theorem to write the distances $b$ , $c$ , $d$ in terms of the altitude. The left and right hand sides of the equation then reduce algebraically to the same expression.^[2]

History

According to Hutton & Gregory (1843 , p. 220), Stewart published the result in 1746 when he was a candidate to replace Colin Maclaurin as Professor of Mathematics at the University of Edinburgh. Coxeter & Greitzer (1967 , p. 6) state that the result was probably known to Archimedes around 300 B.C.E. They go on to say (mistakenly) that the first known proof was provided by R. Simson in 1751. Hutton & Gregory (1843) state that the result is used by Simson in 1748 and by Simpson in 1752, and its first appearance in Europe^{[ clarification needed ]} given by Lazare Carnot in 1803.

Notes

↑ Stewart, Matthew (1746), Some General Theorems of Considerable Use in the Higher Parts of Mathematics, Edinburgh: Sands, Murray and Cochran "Proposition II"
1 2 Russell 1905 , p. 3
↑ Proof of Stewart's Theorem at PlanetMath .

Related Research Articles

<span class="mw-page-title-main">Circle</span> Simple curve of Euclidean geometry

A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. The distance between any point of the circle and the centre is called the radius. The length of a line segment connecting two points on the circle and passing through the centre is called the diameter. A circle bounds a region of the plane called a disc.

<span class="mw-page-title-main">Ellipse</span> Plane curve: conic section

In mathematics, an ellipse is a plane curve surrounding two focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special type of ellipse in which the two focal points are the same. The elongation of an ellipse is measured by its eccentricity $, a number ranging from to .$

In mathematics, the trigonometric functions are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others. They are among the simplest periodic functions, and as such are also widely used for studying periodic phenomena through Fourier analysis.

<span class="mw-page-title-main">Ellipsoid</span> Quadric surface that looks like a deformed sphere

An ellipsoid is a surface that can be obtained from a sphere by deforming it by means of directional scalings, or more generally, of an affine transformation.

In Euclidean geometry, Ceva's theorem is a theorem about triangles. Given a triangle $△ ABC$ , let the lines $AO, BO, CO$ be drawn from the vertices to a common point $O$ , to meet opposite sides at $D, E, F$ respectively. Then, using signed lengths of segments,

In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers, and returns a single number. In Euclidean geometry, the dot product of the Cartesian coordinates of two vectors is widely used. It is often called the inner product of Euclidean space, even though it is not the only inner product that can be defined on Euclidean space.

In geometry, the incircle or inscribed circle of a triangle is the largest circle that can be contained in the triangle; it touches the three sides. The center of the incircle is a triangle center called the triangle's incenter.

In geometry, Thales's theorem states that if $A$ , $B$ , and $C$ are distinct points on a circle where the line $AC$ is a diameter, the angle $∠ ABC$ is a right angle. Thales's theorem is a special case of the inscribed angle theorem and is mentioned and proved as part of the 31st proposition in the third book of Euclid's Elements. It is generally attributed to Thales of Miletus, but it is sometimes attributed to Pythagoras.

In plane geometry, Morley's trisector theorem states that in any triangle, the three points of intersection of the adjacent angle trisectors form an equilateral triangle, called the first Morley triangle or simply the Morley triangle. The theorem was discovered in 1899 by Anglo-American mathematician Frank Morley. It has various generalizations; in particular, if all the trisectors are intersected, one obtains four other equilateral triangles.

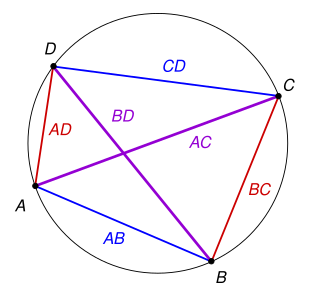
In Euclidean geometry, Ptolemy's theorem is a relation between the four sides and two diagonals of a cyclic quadrilateral. The theorem is named after the Greek astronomer and mathematician Ptolemy. Ptolemy used the theorem as an aid to creating his table of chords, a trigonometric table that he applied to astronomy.

In geometry, the area enclosed by a circle of radius $r$ is $π r 2$ . Here the Greek letter $π$ represents the constant ratio of the circumference of any circle to its diameter, approximately equal to 3.14159.

In geometry, the circumscribed circle or circumcircle of a triangle is a circle that passes through all three vertices. The center of this circle is called the circumcenter of the triangle, and its radius is called the circumradius. The circumcenter is the point of intersection between the three perpendicular bisectors of the triangle's sides, and is a triangle center.

<span class="mw-page-title-main">Small-angle approximation</span> Simplification of the basic trigonometric functions

The small-angle approximations can be used to approximate the values of the main trigonometric functions, provided that the angle in question is small and is measured in radians:

In geometry, Apollonius's theorem is a theorem relating the length of a median of a triangle to the lengths of its sides. It states that the sum of the squares of any two sides of any triangle equals twice the square on half the third side, together with twice the square on the median bisecting the third side. The theorem is named for the ancient Greek mathematician Apollonius of Perga.

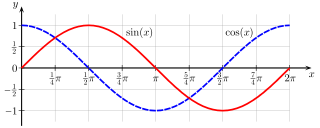
In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side that is opposite that angle to the length of the longest side of the triangle, and the cosine is the ratio of the length of the adjacent leg to that of the hypotenuse. For an angle $, the sine and cosine functions are denoted as and .$

In geometry, a cevian is a line segment which joins a vertex of a triangle to a point on the opposite side of the triangle. Medians and angle bisectors are special cases of cevians. The name "cevian" comes from the Italian mathematician Giovanni Ceva, who proved a well-known theorem about cevians which also bears his name.

In trigonometry, the law of cosines relates the lengths of the sides of a triangle to the cosine of one of its angles. For a triangle with sides $and opposite respective angles and, the law of cosines states:$

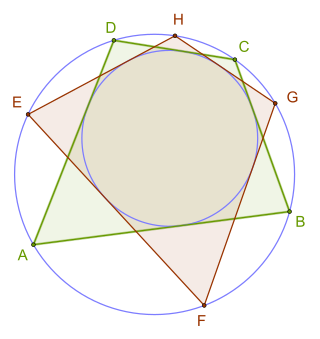
In Euclidean geometry, a bicentric quadrilateral is a convex quadrilateral that has both an incircle and a circumcircle. The radii and centers of these circles are called inradius and circumradius, and incenter and circumcenter respectively. From the definition it follows that bicentric quadrilaterals have all the properties of both tangential quadrilaterals and cyclic quadrilaterals. Other names for these quadrilaterals are chord-tangent quadrilateral and inscribed and circumscribed quadrilateral. It has also rarely been called a double circle quadrilateral and double scribed quadrilateral.

<span class="mw-page-title-main">Pythagorean theorem</span> Relation between sides of a right triangle

In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse is equal to the sum of the areas of the squares on the other two sides.

References

Coxeter, H.S.M.; Greitzer, S.L. (1967), Geometry Revisited, New Mathematical Library #19, The Mathematical Association of America, ISBN 0-88385-619-0
Hutton, C.; Gregory, O. (1843), A Course of Mathematics, vol. II, Longman, Orme & Co.
Russell, John Wellesley (1905), "Chapter 1 §3: Stewart's Theorem", Pure Geometry, Clarendon Press, OCLC 5259132

External links

Weisstein, Eric W. "Stewart's Theorem". MathWorld .
Stewart's Theorem at PlanetMath .

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Stewart, Matthew (1746), Some General Theorems of Considerable Use in the Higher Parts of Mathematics, Edinburgh: Sands, Murray and Cochran "Proposition II"

[Russell-2] 1 2 Russell 1905 , p. 3

[3] Proof of Stewart's Theorem at PlanetMath .

[1]

[2]

[3]