Related Research Articles
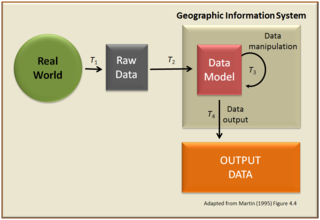
A geographic information system (GIS) is a conceptualized framework that provides the ability to capture and analyze spatial and geographic data. GIS applications are computer-based tools that allow the user to create interactive queries, store and edit spatial and non-spatial data, analyze spatial information output, and visually share the results of these operations by presenting them as maps.

Mathematical statistics is the application of probability theory, a branch of mathematics, to statistics, as opposed to techniques for collecting statistical data. Specific mathematical techniques which are used for this include mathematical analysis, linear algebra, stochastic analysis, differential equations, and measure theory.

Multiple-criteria decision-making (MCDM) or multiple-criteria decision analysis (MCDA) is a sub-discipline of operations research that explicitly evaluates multiple conflicting criteria in decision making. Conflicting criteria are typical in evaluating options: cost or price is usually one of the main criteria, and some measure of quality is typically another criterion, easily in conflict with the cost. In purchasing a car, cost, comfort, safety, and fuel economy may be some of the main criteria we consider – it is unusual that the cheapest car is the most comfortable and the safest one. In portfolio management, managers are interested in getting high returns while simultaneously reducing risks; however, the stocks that have the potential of bringing high returns typically carry high risk of losing money. In a service industry, customer satisfaction and the cost of providing service are fundamental conflicting criteria.

In the design of experiments, optimal designs are a class of experimental designs that are optimal with respect to some statistical criterion. The creation of this field of statistics has been credited to Danish statistician Kirstine Smith.
In statistics, imputation is the process of replacing missing data with substituted values. When substituting for a data point, it is known as "unit imputation"; when substituting for a component of a data point, it is known as "item imputation". There are three main problems that missing data causes: missing data can introduce a substantial amount of bias, make the handling and analysis of the data more arduous, and create reductions in efficiency. Because missing data can create problems for analyzing data, imputation is seen as a way to avoid pitfalls involved with listwise deletion of cases that have missing values. That is to say, when one or more values are missing for a case, most statistical packages default to discarding any case that has a missing value, which may introduce bias or affect the representativeness of the results. Imputation preserves all cases by replacing missing data with an estimated value based on other available information. Once all missing values have been imputed, the data set can then be analysed using standard techniques for complete data. There have been many theories embraced by scientists to account for missing data but the majority of them introduce bias. A few of the well known attempts to deal with missing data include: hot deck and cold deck imputation; listwise and pairwise deletion; mean imputation; non-negative matrix factorization; regression imputation; last observation carried forward; stochastic imputation; and multiple imputation.
Multi-objective optimization is an area of multiple criteria decision making that is concerned with mathematical optimization problems involving more than one objective function to be optimized simultaneously. Multi-objective optimization has been applied in many fields of science, including engineering, economics and logistics where optimal decisions need to be taken in the presence of trade-offs between two or more conflicting objectives. Minimizing cost while maximizing comfort while buying a car, and maximizing performance whilst minimizing fuel consumption and emission of pollutants of a vehicle are examples of multi-objective optimization problems involving two and three objectives, respectively. In practical problems, there can be more than three objectives.
Polynomial chaos (PC), also called Wiener chaos expansion, is a non-sampling-based method to determine the evolution of uncertainty in a dynamical system when there is probabilistic uncertainty in the system parameters. PC was first introduced by Norbert Wiener using Hermite polynomials to model stochastic processes with Gaussian random variables. It can be thought of as an extension of Volterra's theory of nonlinear functionals for stochastic systems. According to Cameron and Martin such an expansion converges in the sense for any arbitrary stochastic process with finite second moment. This applies to most physical systems.
Group method of data handling (GMDH) is a family of inductive algorithms for computer-based mathematical modeling of multi-parametric datasets that features fully automatic structural and parametric optimization of models.
The dominance-based rough set approach (DRSA) is an extension of rough set theory for multi-criteria decision analysis (MCDA), introduced by Greco, Matarazzo and Słowiński. The main change compared to the classical rough sets is the substitution for the indiscernibility relation by a dominance relation, which permits one to deal with inconsistencies typical to consideration of criteria and preference-ordered decision classes.
In applied mathematics and decision making, the aggregated indices randomization method (AIRM) is a modification of a well-known aggregated indices method, targeting complex objects subjected to multi-criteria estimation under uncertainty. AIRM was first developed by the Russian naval applied mathematician Aleksey Krylov around 1908.
SMAA may refer to:
In probability theory, a Markov model is a stochastic model used to model randomly changing systems. It is assumed that future states depend only on the current state, not on the events that occurred before it. Generally, this assumption enables reasoning and computation with the model that would otherwise be intractable. For this reason, in the fields of predictive modelling and probabilistic forecasting, it is desirable for a given model to exhibit the Markov property.
Suitability Analysis is the process and procedures used to establish the suitability of a system – that is, the ability of a system to meet the needs of a stakeholder or other user.
The Preference Ranking Organization METHod for Enrichment of Evaluations and its descriptive complement geometrical analysis for interactive aid are better known as the Promethee and Gaia methods.

The European Working Group on Multiple Criteria Decision Aiding is a working group whose objective is to promote original research in the field of multicriteria decision aiding at the European level.
In multiple criteria decision aiding (MCDA), multicriteria classification involves problems where a finite set of alternative actions should be assigned into a predefined set of preferentially ordered categories (classes). For example, credit analysts classify loan applications into risk categories, customers rate products and classify them into attractiveness groups, candidates for a job position are evaluated and their applications are approved or rejected, technical systems are prioritized for inspection on the basis of their failure risk, etc.
In queueing theory, a discipline within the mathematical theory of probability, a fluid queue is a mathematical model used to describe the fluid level in a reservoir subject to randomly determined periods of filling and emptying. The term dam theory was used in earlier literature for these models. The model has been used to approximate discrete models, model the spread of wildfires, in ruin theory and to model high speed data networks. The model applies the leaky bucket algorithm to a stochastic source.
The VIKOR method is a multi-criteria decision making (MCDM) or multi-criteria decision analysis method. It was originally developed by Serafim Opricovic to solve decision problems with conflicting and noncommensurable criteria, assuming that compromise is acceptable for conflict resolution, the decision maker wants a solution that is the closest to the ideal, and the alternatives are evaluated according to all established criteria. VIKOR ranks alternatives and determines the solution named compromise that is the closest to the ideal.
Measuring attractiveness through a categorical-based evaluation technique is the goal of the MACBETH approach that was designed by Carlos António Bana e Costa, from the University of Lisbon, in cooperation with Professor Jean-Claude Vansnick and Dr. Jean-Marie De Corte, from the Université de Mons.
Stochastic scheduling concerns scheduling problems involving random attributes, such as random processing times, random due dates, random weights, and stochastic machine breakdowns. Major applications arise in manufacturing systems, computer systems, communication systems, logistics and transportation, machine learning, etc.
References
- ↑ Lahdelma, R.; Salminen, P. (2001). "SMAA-2: Stochastic Multicriteria Acceptability Analysis for Group Decision Making". Operations Research. 49 (3): 444–454. CiteSeerX 10.1.1.138.4807 . doi:10.1287/opre.49.3.444.11220.
- ↑ Sousa R., Yevseyeva I., Pinto da Costa J.F., Cardoso J.S. (2013). Multicriteria models for learning ordinal data: A literature review. In Yang X.S. Artificial Intelligence, Evolutionary Computing and Metaheuristics: In the Footsteps of Alan Turing. Studies in Computational Intelligence 427, Springer.
- ↑ Tervonen, T.; Figueira, J. (2008). "A survey on stochastic multicriteria acceptability analysis methods". Journal of Multi-Criteria Decision Analysis. 15 (1–2): 1–14. doi: 10.1002/mcda.407 .
- ↑ Tervonen, Tommi. "Open source decision aiding software for real-life applications". SMAA.fi. Retrieved 17 December 2016.